Лабораторная работа № 1. Лабораторная работа № 1
Лабораторная работа № 1
«Определение модуля упругости костной ткани»
Цель работы: Изучение упругих и прочностных свойств тканей организма. Используя универсальную установку определить модуль упругости образца по деформации изгиба.
Вопросы теории (исходный уровень):
1. Упругие, вязкие и вязкоупругие среды.
2. Механические характеристики и модели упругих, вязких и вязкоупругих сред.
3. Механические свойства:
- костной ткани,
- мышц,
- сухожилий,
- сосудов.
Содержание занятия:
1. Выполнить работу по указаниям в руководстве к данной работе.
2. Оформить отчет.
3. Защитить работу с оценкой.
4. Решить задачи.
Задачи
Какая сила необходима для разрушения при сжатии бедренной кости диаметром 30 мм с толщиной стенок 3 мм, если предел прочности кости 1,4 · 108 н/м2?
Определить толщину стенки большой берцовой кости диаметром 28 мм, если ее разрыв произошел при нагрузке 23,1· 103 н. Предел прочности кости принять равным 9,8 · 107 н/м2.
Определить абсолютное удлинение сухожилия длиной 4 см и диаметром 6 мм под действием силы 31,4 н. Модуль упругости сухожилия принять равным 109 н/м2.
Мышца длиной 10 см и диаметром 1 см под действием груза 49 н удлинилась на 7 мм. Определить модуль упругости мышечной ткани.
Модуль упругости протоплазменных нитей, получившихся вытягиванием протоплазмы у некоторых типов клеток с помощью микроигл, оказывается равным 9 · 103 н/м2 при комнатной температуре. Определить напряжение, действующее на нить при растяжениях, не превышающих 20% ее первоначальной длины.
Какая работа совершается при растяжении на 1 мм мышцы длиной 5 см и диаметром 4 мм? Модуль Юнга для мышечной ткани принять равным 9,8· 107 н/м2.
Найти потенциальную энергию, приходящуюся на единицу объема кости, если кость растянута так, что напряжение в ней составляет 3 · 109 н/м2. Модуль упругости кости принять равным 22,5 109 н/м2.
Лабораторная работа № 1
« ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ КОСТИ ПО ИЗГИБУ»
Приборы и принадлежности: 1) индикатор длин; 2) штангенциркуль;
3) миллиметровая линейка длиной 30 см; 4) две опоры со стальными призмами,
5) пластина, вырезанная из бедренной кости; 6) кусок бедренной или плечевой кости длиной 20—25 см; 7) пластина органического стекла; 8) алюминиевая и стеклянная трубки длиной 30 см; 9) набор грузов по 50 и 100 г (всего 5 кг).
Изучение упругих и прочностных свойств тканей организма имеет большой практический интерес. Например, знание упругих характеристик костей необходимо в хирургической практике (подбор нагрузок при вытяжениях). Прочность костей — показатель, без которого не может обойтись судебно-медицинская экспертиза. Для диагностики заболеваний сердечно-сосудистой системы используется определение модуля упругости стенок кровеносных сосудов. Ознакомление с элементами учения о сопротивлении материалов представляет особый интерес для студентов стоматологического факультета, так как зубной протез — это конструкция, прочность и надежность которой обеспечивается учетом законов деформаций.
Деформациями называют изменения формы и объема тел под действием различных сил. В зависимости от действующих сил различают следующие виды деформации: растяжение, сжатие, сдвиг, кручение и изгиб. Всем твердым телам присущи два вида деформаций: упругая, когда после прекращения действия сил деформация полностью исчезает, и остаточная (пластическая), когда после прекращения действия сил деформация полностью не исчезает. Деформация сохраняет характер упругой только для малых нагрузок до предельного ее значения, называемого пределом упругости, после чего она переходит в пластическую. Исследуя упругие деформации тел, английский физик Гук установил следующий закон: удлинение Dl тела прямо пропорционально приложенной к нему силе Р, его первоначальной длине l и обратно пропорционально площади поперечного сечения S, т. е.
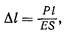 (1)
(1)
где Е — модуль упругости, или модуль Юнга. Равенство (1) можно представить в виде
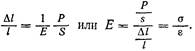
Отношение 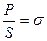 называется напряжением,
называется напряжением, 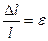 — относительным удлинением. При Dl = l получим
— относительным удлинением. При Dl = l получим 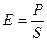 , т. е. модуль Юнга представляет напряжение, при котором длина образца удваивается (l + Dl = 2l ). Фактическое удвоение длины можно получить у резины и ряда полимерных материалов. Для других материалов нарушение прочности происходит раньше, чем длина образца удвоится. Упругие константы иногда удобнее определять не по деформации растяжения, а по изгибу образца. В деформации изгиба сжатия в одной части образца комбинируются с растяжениями в другой его части. В отличие от продольных напряжений растянутых (или сжатых) образцов напряжения при изгибе будут поперечными, т. е. перпендикулярными к их длине. Мерой деформации в этом случае служит стрела прогиба, т. е. наибольшее отклонение одной из точек образца от первоначального положения.
, т. е. модуль Юнга представляет напряжение, при котором длина образца удваивается (l + Dl = 2l ). Фактическое удвоение длины можно получить у резины и ряда полимерных материалов. Для других материалов нарушение прочности происходит раньше, чем длина образца удвоится. Упругие константы иногда удобнее определять не по деформации растяжения, а по изгибу образца. В деформации изгиба сжатия в одной части образца комбинируются с растяжениями в другой его части. В отличие от продольных напряжений растянутых (или сжатых) образцов напряжения при изгибе будут поперечными, т. е. перпендикулярными к их длине. Мерой деформации в этом случае служит стрела прогиба, т. е. наибольшее отклонение одной из точек образца от первоначального положения.
Графическое изображение распределения значений каких-нибудь величин по длине образца называется эпюрой.
На рис. 8, а, б, в показаны (сверху вниз): эпюры деформаций, поперечных напряжений и изгибающих моментов образца, свободно лежащего на опорах, под действием нагрузки, приложенной к его середине.
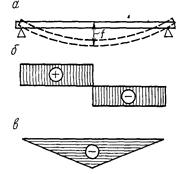
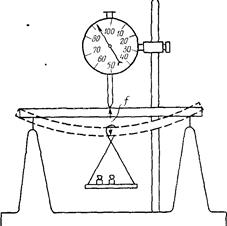
Рис. 8 Рис. 9
Установка для определения модуля упругости по деформации изгиба показана на рис. 9. Образец свободно укладывается на две стальные призмы, которыми заканчиваются опоры. Посредине образца подвешивается чашка для грузов. Прогиб измеряется с помощью индикатора длин. Для модуля упругости образца в виде пластины (пластины кости, органического стекла) теория дает следующее выражение:
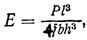 (2)
(2)
где Р —нагрузка; l — длина образца (расстояние между опорами); f —стрела прогиба; b — ширина образца; h — высота (направление нагрузки). Для образца в форме трубки теория дает выражение:
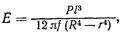 (3)
(3)
где R — внешний; r — внутренний диаметр трубки.
Расстояние между опорами измеряют миллиметровой линейкой, линейные размеры — штангенциркулем. Измерения делают в нескольких местах вдоль образца и берут их средние значения. Все размеры выражают в метрах, нагрузку Р — в ньютонах.
Порядок работы
1. Исследование зависимости стрелы прогиба от нагрузки. Образец располагают на опорах так, чтобы он плотно касался призм. Хомут чашки для гирь устанавливают посредине образца. Вертикальный стержень индикатора перемещений приводят в соприкосновение с верхней поверхностью середины образца, устанавливая стрелку индикатора в нулевом положении. Постепенно, без толчков, нагружают образец, отмечая для каждого груза соответствующую стрелу прогиба. Определение стрелы прогиба нужно проводить только в области упругих деформаций. Поскольку наложение даже небольших нагрузок вызывает перемещения стрелки индикатора длин не плавно, а рывками, то определение зависимости стрелы прогиба от нагрузки можно исследовать, если вместо грузов на чашку весов поставить сосуд, в который с помощью шланга с зажимом наливают малой струйкой воду. Сосуд заранее проградуирован в ньютонах. Останавливая зажимом движущийся поток воды на определенных делениях нагрузок, отмечают соответствующие значения стрелы прогиба. Результаты опыта заносят в таблицу.
| Материал | Нагрузка/стрела прогиба | |||||||||||
| Кость | ||||||||||||
| Дюралюминий |
По найденным значениям стрелы прогиба и соответствующим нагрузкам строят график. Для этого по оси ординат откладывают нагрузку, а по оси абсцисс — стрелу прогиба. При правильно выполненном опыте график представляет прямую линию.
2. Определение модуля упругости кости и других материалов. В формулы (2) или (3) подставляют средние значения размеров образца, вместо Р — сумму всех нагрузок, вместо f—сумму всех стрел прогиба, что равносильно нахождению их средних значений, и вычисляют Е. Значения модулей упругости некоторых материалов приведены в табл. 8 приложений.
