Кинетика биохимических реакций.

ОПРЕДЕЛЕНИЕ СКОРОСТИ И МОЛЕКУЛЯРНОСТИ

РЕАКЦИЙ.

Цель работы:

Обучаемый должен знать:

1.Основные модельные типы химических реакций и методы их изучения.

2. Основные законы химической кинетики.

3. Кинетические допущения в гетерогенных системах.

4. Особенности применения законов кинетики в биологических системах.

Обучаемый должен уметь:

1. Наблюдать за протеканием реакции и обработать кинетические данные для уточнения молекулярности и механизма реакции.

2. Вывести уравнения кинетики модельных реакций.

3. Назвать и обосновать допущения применяемые для гетерогенных систем.

4. Использовать стандартные кинетические методы для конкретных реакций.

Практическое значение работы:

Химическая кинетика позволяет оценить закономерности сложных процессов в различных технологических и биологических системах. Особенностью реакций в биологических системах является постоянная многостадийность и участие в большинстве элементарных актов биологических катализаторов-ферментов. Нарушение правильной последовательности и кинетики стадий приводит к болезненным изменениям в организме. Знание основных закономерностей кинетики позволяет правильно оценить причины болезней и помогает выбрать пути их скорейшего излечения.

Бюджет времени

На изучение темы отводится 6,5 часов, из них 2 часа лекций, 2 часа лабораторные занятия и 2,5 часа на самоподготовку.

Литература

1. Эмануэль И.М., Кнорре Д.Г. Курс химической кинетики.- М.: Высшая школа, 1974.- 400 с.

2. Шмид Р., Сапунов В.Н. Неформальная кинетика. В поисках путей химических реакций.- М.: Мир, 1985.- 264 с.

3. Еськов В.М., Филатова О.Е. Статистическая обработка результатов измерений по естествознанию и экологии (СОРИПЕЭ).- Сургут, 1998.-64 с.

методические указания по I этапу “самоподготовка”

Цель этапа: 1. Повторить исходную информацию по законам и допущениям химической кинетики.

2. Изучить новую информацию по методам обработки кинетических данных.

Исходный уровень знаний. Для изучения темы и выполнения работы обучающийся должен повторить данные по модельным кинетикам реакций и методам статистической обработки результатов. Следует обратить особое внимание на особенности применения кинетических уравнений для гетерогенных систем. Для биохимических реакций вспомнить уравнения кинетики ферментативных реакций.

Изучив блок информации и литературу, обучаемый должен ответить на следующие вопросы и решить задачи.

1.Что такое химическая кинетика?

2.Что такое порядок и молекулярность химической реакции? Когда они совпадают?

3.Чем отличаются простые реакции от сложных?

4.Что такое катализатор? В чем его отличие от инициатора?

5.Как определить порядок реакции и порядок по компоненту? В каком случае возможно получение истинного значения порядка реакции из стехиометрии реакции?

6.Что такое энергия активации?

7.Что такое катализ? Каков механизм действия катализаторов? В чем различие гетерогенного катализа от гомогенного?

8.Каковы особенности ферментов, как биологических катализаторов? Используйте знания биологии для объяснения: а) потребности животных в витаминах; б) действия ядов и противоядий, в частности CN^- -ионов, кислот и щелочей; в) жизненного цикла холоднокровных и теплокровных животных.

9.Почему при некоторых болезнях желудка рекомендуется перед едой принимать препараты соляной кислоты?

10.Какие особенности живых организмов следует обязательно учитывать при кинетическом исследовании биологических реакций?

11.Почему расщепление компонентов пищи происходит в основном: углеводов- ферментами слюны, белков- ферментами желудочного сока, жиров- в кишечнике? Используйте знания о рН биологических жидкостей.

12. Белковая пища измельчается зубами в ротовой полости, подвергается воздействию ферментов желудочного сока, причем особенно активному у желудочной стенки, всасывается через кишечную стенку по механизму активной диффузии, переносится кровью в ткани, проникает активной диффузией через клеточную стенку, где в митохондриях образуются специфические белки. Определите проходящие процессы с точки зрения гетерогенности и гетерофазности.

13.В сосуд вместимостью 5л ввели чистый этан С₂Н₆ при Р=1 атм и Т=300 К°. сосуд быстро нагрели до 1000 К°, при этой температуре проходит реакция

С₂Н₆®С₂Н₄+Н₂

Изменения концентрации этана приведены в таблице.

t,c
С, ммоль/л	40,65	24,66	14,95	9,07	5,50	3,34

Выберите правильные ответы на вопросы:

а) Каков порядок реакции: 1)0,5; 2)1; 3)2; 4)3; 5)другой.

б) Чему равна константа скорости реакции: 1)1; 2)0,204; 3)20,4; 4)0,49; 5)другая.

в)Каков период полупревращения t_1/2 (в секундах): 1)0,07; 2)10; 3)20,4; 4)0,49; 5)другой.

г) Чему равна константа скорости при 1250 К°, если энергия активации равна 83,1 КДж/моль: 1)4,9; 2)0,362; 3)210; 4)0,075; 5)другая. Укажите размерность.

д)Какое давление (в атм) установилось бы в сосуде при 1000 К°, если бы этан не подвергался бы разложению: 1)2,65; 2)5,00; 3) 3,33; 4)3,66; другое.

е)Чему равна константа равновесия К_р (атм) при 1000 К°: 1)0,835; 2)1,67; 3)2,79; 4)1,00; 5)другая.

Методические указания по II этапу:

"Выполнение работы"

1.Сделайте для исследования водную вытяжку из почвы. Для этого насыпьте в стакан образец почвы, залейте её дистиллятом и оставьте его на 1-2 дня для перехода почвенных кислот из частиц почвы в раствор. В полученной вытяжке определите рН и добавьте порошок мела или известняка. Результаты представьте в таблице 1. Признаком завершения реакции можно считать достижение рН= 8-9.

Таблица 1.

t					¼	i
pH

2.Выберите промежуток времени между измерениями, что бы изменения рН были 0.2- 0.3, количество точек должно быть не меньше 5.

3. Обработку результатов проведите следующим образом. Концентрация протонов по определению равна 10^-рН, DC_i=C_i-C_i-1, Dt=t_i-t_i-1. Составьте таблицу 2. для расчета.

Таблица 2.

lg(-[DC]/[ Dt])	C1	C2	C3	¼	Ci
lg[C]=-pH	pH1	pH2	pH3	¼	pHi

Постройте график по точкам. Непосредственное построение графика обосновано при достаточном количестве точек, если их количество 4-5, обработка по МНК значительно точнее. Кинетические характеристики получаются из графика (порядок равен тангенсу наклона прямой и логарифм константы равен значению в точке пересечения прямой с осью lg(-[DC]/[ Dt])) или по МНК (порядок равен коэффициенту перед переменной (lg[C]) и логарифм константы равен свободному члену). При подсчете кинетических констант обязательно учитывайте количество верных знаков и правила округления величин.

Методические указания по III этапу:

“Получение зачета по лабораторной работе”

После выполнения 1 и 2 этапов обучаемый должен заполнить протокол и подписать его у преподавателя, а затем оформить зачет в тетради, обратив особое внимание связь наблюдаемых в растворе явлений с механизмом протекающих реакций (целесообразно использовать ЭВМ для первичной статистической обработки) и отчитаться у преподавателя за всю работу. В этом случае обучаемый получает зачет.

Блок информации.

Химическая кинетика- раздел физической химии, посвященный исследованию закономерностей протекания химических процессов во времени.

Запишем химический процесс в общем виде

n₁A₁+n₂A₂+¼+n_kA_k® n₁`B<sub>1</sub>+n<sub>2</sub>`B₂+¼+n_k`B_k

где n₁- стехиометрические коэффициенты исходных, а n₁`- конечных веществ, A_k- исходные вещества, B_k- продукты реакции. Введем следующие определения:

Скоростью химической реакции называется количество вещества превращенное в данной реакции за единицу времени

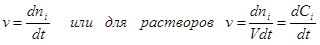(1)

Скорость всегда положительна, поэтому если используем изменения концентраций исходных, перед производной следует ставить минус. Очевидно, что в реакцию могут вступить только молекулы, которые сталкиваются. Число столкновений прямо пропорционально числу молекул, поэтому скорость реакций должна быть пропорциональна концентрации реагентов, т.е. в общем случае

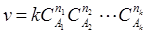(2)

где k- константа реакции равная скорости при единичных концентрациях реагентов; С_Аk- концентрации реагирующих веществ; n_k- порядок по веществу A_k, который требует дополнительного определения.

Реакцию называют простой, если продукт получается в одну стадию, с преодолением одного энергетического барьера, т.е. конечные продукты получаются из исходных сразу, без промежуточных. Если доказана многостадийность и присутствие промежуточных продуктов то реакция сложная. Можно выделить стадии обратимые, когда переходы исходных и конечных веществ взаимно возможны и необратимые, когда исходные продукты целиком переходят в некоторые но определенные

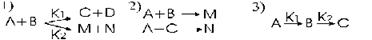
Рис.1 Типы элементарных процессов: 1)параллельные; 2)сопряженные;3)последовательные.

конечные. Стадии могут протекать параллельно(рис.1,1), когда исходные продукты одновременно превращаются по нескольким путям, со своими кинетиками и продуктами; они могут быть сопряженными(рис.1,2), когда одна реакция может протекать только совместно с другой, если продукт M можно получить только в присутствии С, т.е. обязательно наличие А,В и С, то С называют индуктором; последовательными(рис.1,3), когда конечные продукты одной стадии становятся исходными для другой.

Особый вид сложных реакций цепные, когда одной из реагирующих частиц является радикал (частица с неспаренным электроном) со своей последовательностью стадий: 1)зарождения- возникновения радикалов из валентно насыщенных молекул; 2)продолжения- стадия с сохранением количества неспаренных электронов; 3)разветвления- исходный радикал рождает несколько; 4)обрыв- уничтожение или появление вместо нестабильных и активных в реакции радикалов малоактивных. Выделяют процессы разветвленные, когда имеется хотя бы одна стадия ветвления и неразветвленные, когда они отсутствуют.

Реакции характеризуются количеством частиц в ней участвующих. Если в элементарном акте участвует одна частица, то реакцию называют мономолекулярной (рис.2,1), если две- бимолекулярной (рис.2,2), если три- тримолекулярной (рис2,3).

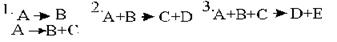
Рис.2

Для элементарных реакций молекулярность равна сумме стехиометрических коэффициентов реагентов и совпадает с общим порядком реакции, т.е мономолекулярная реакция имеет первый порядок, бимолекулярная- второй, тримолекулярная- третий. Для многостадийных реакций, даже с малой суммой стихеометрических коэффициентов установление порядка общего для реакции или для каждого реагента требует специального исследования. Если сумма коэффициентов превышает три, можно обоснованно утверждать сложность механизма, т.к. вероятность столкновения больше трех частиц чрезвычайно мала.

Наиболее просто выглядят уравнения для односторонних необратимых процессов. Реакция первого порядка

А®В или А®В+С

Описывается кинетическим уравнением

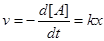(1)

Разделив переменные и проинтегрировав, получим

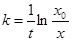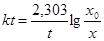или (2)

где k- константа скорости, t- время, x₀- начальная концентрация, x-конечная концентрация А в момент времени t. Уравнение можно представить в виде

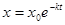(3)

Реакцию второго порядка вида

2А®C+D

описывает кинетическое уравнение

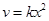(4)

константа вычисляется

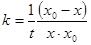(5)

Для реакции

А+В®С+Е

уравнение

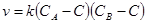(6)

и константа вычисляется

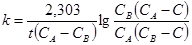(7)

где С_А и С_В- начальные концентрации веществ А и В, а С- расход их к моменту t.

Для реакции третьего порядка вида

3А®В+С

уравнение

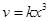(8)

и константа равна

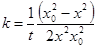(9)

Скорость всегда имеет размерность [количество (концентрация),Х]/ [время,t], поэтому константы первого порядка имеют размерность [t]^-1, второго- [x]^-1[t]^-1, третьего- [x]^-2[t]^-1 и т.д. Исходя из наиболее распространенных выражений концентрации размерность констант: первого порядка- сек^-1, второго- л/(моль×сек), третьего- л²/(моль²×сек). Сравнивать константы разных порядков нельзя, это разные физические величины.

Среди констант, полезных для исследования реакций, определяют времена для различных степеней превращения (таблица 3). Используя их можно определять порядки реакций, близкие

Таблица 3.

Превращение   Порядок реакции	1/4	1/3	1/2	3/4
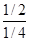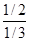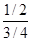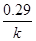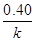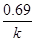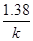					2.4	1.7	0.5
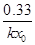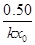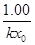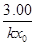					3.0	2.0	0.3
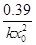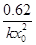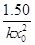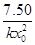					3.8	2.4	0.2

к модельным.

На реальной схеме рассмотрим конкретные примеры. Реакция разложения перекиси водорода в присутствии Fe²⁺ протекает следующим образом

2Fe²⁺ +H₂O₂ +2H⁺® 3Fe³⁺ + 2H₂O

по следующим стадиям

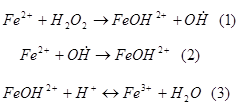[I.1]

Бензол в смеси с перекисью достаточно устойчив и продуктов окисления не появляется, но в смеси с солью Fe²⁺ обнаруживается фенол (C₆H₅OH) и дифенил(С₆Н₅-С₆Н₅). Механизм состоит из следующих стадий

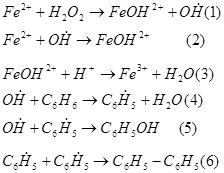[I.2]

Продукты окисления бензола появляются только в присутствии солей железа, т.е Fe²⁺ является индуктором, видно, что роль индуктора состоит в открытии новых реакционных путей ( в нашем случае создание инициирующих радикалов).

Для цепных реакций самые известные примеры- реакции окисления и реакция получения хлороводорода. Получение HCl- неразветвленный цепной процесс, его схема

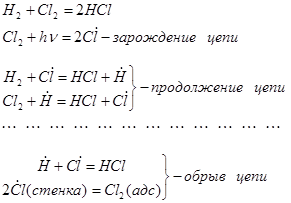[I.3]

Реакции окисления включают стадии ветвления

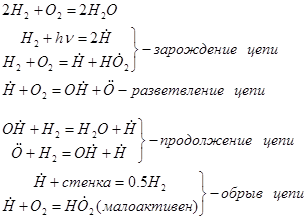[I.4]

Из приведенного видно, что многие внешне простые процессы протекают через последовательность стадий, т.е. являются сложными. Для сложных процессов общие кинетические характеристики (порядок, константы скорости) могут быть только формальными и совпадения с модельными порядками и константами чисто случайны. Определения их одна из важнейших стадий исследования механизма реакций.

Большая часть реакций протекает с большими скоростями и через малоустойчивые промежуточные соединения, поэтому определение механизма реакции практически всегда сложная проблема. Проще всего её решить для случая средних скоростей накопления продуктов или расходования исходных реагентов. Измерять и подставлять в кинетическое уравнение можно любую величину, однозначно связанную с концентрацией любого из реагентов (остальные определяют по стихеометрии реакции). Можно измерять объём для газов, в растворе можно измерять рН, интенсивность окраски, поляризацию света, твердые тела можно просто взвешивать; можно проводить измерения прямо в реакторе, можно отбирать пробы и определять всё в них, но тогда принимают специальные меры для сохранения неизменным состава пробы до исследований.

Реальные реакции чаще всего проводят в специально подобранных условиях, позволяющих упростить получение результата. Простейший способ исследования кинетических констант сложных реакций состоит в проведении реакции, когда концентрации всех веществ (кроме целевого) достаточно велики, что бы считать их неизменными на протяжении всей реакции. Тогда кинетическое уравнение упрощается до вида

v = k`[C]ⁿ (10)

где k`- псевдоконстанта реакции, равная произведению истинной на концентрации остальных веществ в реакционной смеси, а n- порядок реакции по исследуемому веществу. Прологарифмировав, получим

lg v = n lg [C] + lg k` (11)

Записав скорость как v=DC/Dt, мы получаем рабочую формулу для определения порядка и константы нашей реакции. Следует построить график линейной функции

lg(-[DC]/[ Dt])= n lg[C] + lgk`

и величины получатся из графика: порядок равен тангенсу наклона прямой и логарифм константы равен значению в точке пересечения прямой с осью lg(-[DC]/[ Dt]). Можно провести линеаризацию по методу наименьших квадратов (МНК), тогда порядок равен коэффициенту перед переменной (lg[C]) и логарифм константы равен свободному члену.

Для исследования кинетики в реакционных смесях разработаны другие методы линеаризации в специально подобранных координатных осях. Если есть достаточные основания, можно использовать метод подбора. Для кинетики близкой к модельным можно построить график в координатах: для первого порядка lgx-t, для второго- (1/x)-t, для третьего- (1/x²)-t. Зависимость близкая к линейной позволяет считать верным определенный закон. Существуют реакции так называемого нулевого порядка, когда концентрации настолько велики, что скорость не зависит от времени, прямая получается в координатах х-t. Кроме того, определенные выводы о кинетике позволяет сделать соотношение времен для стандартных глубин превращения (таб.3).

Реакции любых порядков позволяют исследовать другие методы.

Вычисление порядка по времени полупревращения проводится на следующей основе. Интегрируя стандартное уравнение

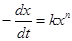(12)

получаем для n¹1

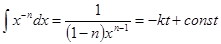(13)

где константа вычисляется из условия, что при t=0 x=x₀

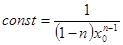(14)

и окончательно

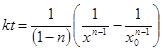(15)

Период полупревращения определяется из условия х=0,5х₀

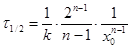(16)

Видно, что t_1/2- функция х₀; прологарифмировав получим основное уравнение метода

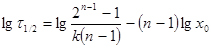(17)

Для получения результата проводят реакцию при нескольких начальных концентрациях, полученные точки наносят на график lgt_1/2-lgx₀ и из линейной зависимости определяют порядок реакции по компоненту.

Можно обрабатывать и реальные кинетические кривые. Получив экспериментальные точки, наносят их на плоскость x(C)-t и проводят линию наилучшим образом огибающую их все именно её обрабатывают описанными способами; обработка линии, а не полученных точек снижает влияние случайных ошибок. Для метода полупревращений такая обработка полностью корректна только для целочисленных порядков. Рассмотрим реакционную кривую анаэробного гликолиза глюкозы в мышцах (рис.3)

С₆Н₁₂О₆ ® 2 СН₃СН(ОН)СООН

Реакция по определению мономолекулярная, порядок определим способами описанными выше. По кривой найдем t_1/2, t_1/3, t_3/4, t_1/4 и найдем значения для сравнения с таб.3. Видно, что числа наиболее близки для соотношений реакции первого порядка (рис.3.I), хотя отличия дают основания подозревать нецелочисленность порядка. Используя кривую, как источник точек для метода полупревращений (рис.3.II), тоже получим свидетельства в пользу первого порядка реакции, но в дополнение к этому можем оценить константу реакции из свободного члена уравнения МНК

lg t_1/2= -7.02×10^-2lgC₀+1.47

Учтя, что константа перед lgC₀ равна 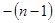подставив это число в выражение для свободного члена в (17), получаем k=1.6×10^-2. Для построения графика зависимости скорости от концентрации (рис.3.III) используем все точки предыдущих методов и точки концентраций, кратных 0.5 из реакционной кривой. Обработка по МНК дает следующее уравнение

,

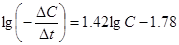где 1.42- порядок реакции, а (-1.78)- десятичный логарифм константы реакции, т.е. k=1.7×10^-2. Величины константы,

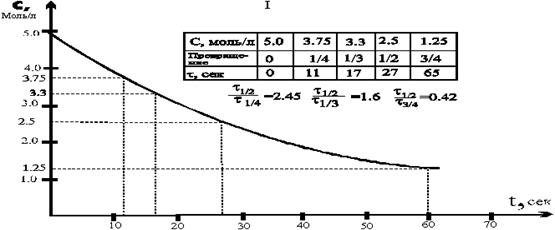
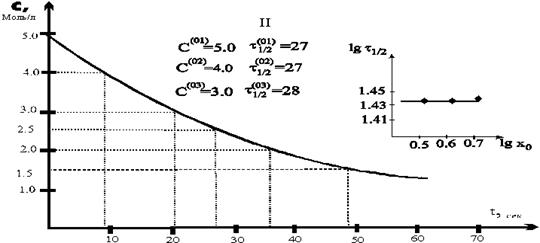
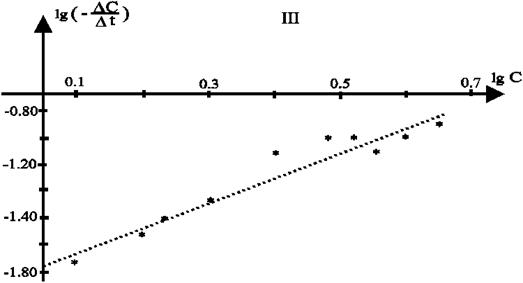
Рис.3 Определение порядка реакции: I- по времени для стандартных степеней превращения, II- по периодам полупревращения, III- по скоростям.

полученные из рис.3.(II,III) вполне совместны и для полученных из кривой с небольшим масштабом сходимость более чем достаточна,

но величины порядков разные. Учитывая неполную применимость метода полупревращений к обработке кривых и отклонения величин рис.3.I от табличных, можно настаивать на данных рис.3.III, как полученных более универсальным методом на основе большего количества точек.

Определив порядок по одному компоненту из псевдоконстант можно определить порядки для других компонентов. Проведя реакцию с определенным набором постоянных концентраций компонентов, мы из зависимости вида (10) получаем набор k` порядок по C_i определяем из линейной зависимости

lg k` = lg k + n_ilg C_i (18)

определяем порядок по C_i (n_i) и истинную константу k.

Энергетические аспекты химической кинетики

Скорость реакции сильно зависит от температуры её проведения. Концентрации реагентов от температуры зависят мало и очевидно, что от температуры зависит величина кинетической константы, эмпирически зависимость описывается правилом Вант- Гоффа

k^(t+10)/k^t= g= 2¸ 4»3

где g- температурный коэффициент. В небольших промежутках температур он сохраняет постоянство и константа может рассчитываться по уравнению

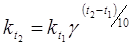
Для точных расчетов применяют уравнение Аррениуса

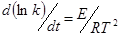, (19)

где R- универсальная газовая постоянная (8.31 Дж/К×моль), k- кинетическая константа, T- температура градусах Кельвина, E- константа, имеющая размерность энергии и называемая

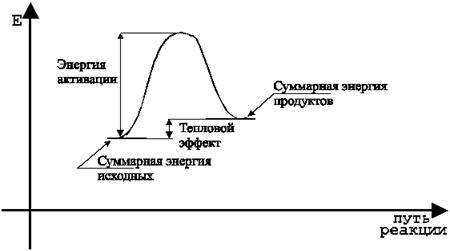
Рис.4

энергией активации. Предполагается, что энергия активации равна избытку энергии, которым должна обладать частица по сравнению со средней энергией при данной температуре, что бы вступить в реакцию, она совпадает с ранее уже упомянутым энергетическим барьером (рис.4) и так же имеет очевидный физический смысл только для простых реакций, для многостадийных процессов это некая эмпирическая усредненная величина. Интегрируя уравнение Аррениуса, получим

ln k= (-E/RT)+const или k= A×e^-E/RT (20)

где А- эмпирический коэффициент, называемый предэкспоненциальным множителем, который показывает вероятность вступления в реакцию частицы, обладающей необходимой энергией, т.к. для реакции важны не только энергии реагирующих частиц, но и соотношение их внутримолекулярных (орбитали, моменты инерции и т.д.) характеристик. Возможная зависимость энергии активации от температуры для биологических процессов не принципиальна из-за узкого диапазона температур биологических процессов. Достаточно точно энергию активации можно вычислить проведя реакцию при двух различных температурах и подставив величины констант и температур в уравнение

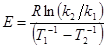(21)

Для строгого вычисления энергии активации желательно получение характеристик не менее чем при 4-5 температурах и построение графика в координатах ln k- (1/T) (аррениусовских) (рис.5). Прямая линия, проведенная через точки, отсекает на оси ln k отрезок равный ln A, а тангенс угла наклона позволяет получить величину Е по формуле

A= -R×arctg j (22)

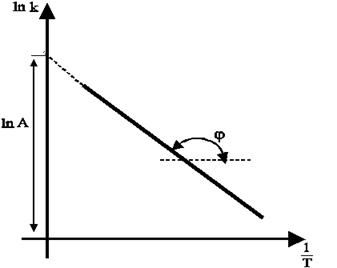
Рис.5

Учет гетерогенности реакционных систем

В зависимости от наличия границ раздела фаз нахождения реагентов и протекания реакций выделяют гомогенные, в случае нахождения реагентов и протекания реакций в границах одной фазы и гетерогенные, если хотя бы один компонент или стадия процесса происходит на границе или в разных фазах. Выделяют гомофазные процессы, когда исходные, стабильные промежуточные и конечные продукты находятся в границах одной фазы и гетерофазные, если названные вещества образуют более чем одну фазу. Возможны различные комбинации: нейтрализация кислот в растворах- гомогенно- гомофазная реакция, окисление жидких углеводородов кислородом воздуха- гетерогенно- гомофазная реакция (окисление идет только кислородом, растворившимся в жидкой фазе), примером гомогенно- гетерофазной реакции может служить реакция гидрирования непредельных углеводородов на катализаторе, гетерогенно- гетерофазной- реакция оксида кальция с водой.

Применение общих кинетических закономерностей к гетерогенным процессам имеет следующие особенности:

1. Закон действующих масс для многофазных процессов заменяется законом действующих площадей. Очевидно, что реакция может идти только при контакте исходных реагентов, т.е. с ростом площади контакта реакция резко активизируется и концентрации для твердых тел или жидкостей для реакций через границу раздела фаз заменяются площадью границы фаз; если реакция протекает на выделенных местах поверхности, используют понятие активной поверхности. Поэтому твердые вещества вводят в реакцию в виде максимально измельченной пудры, газы барботируют (продувают) через жидкость мелкими пузырьками, если реакция протекает на границе несмешивающихся жидкостей, создают устойчивую эмульсию для создания достаточной площади контакта. Для биохимических реакций пищеварения можно упомянуть эмульгирующее влияние желчных кислот, повышающих площадь контакта пищи и пищеварительных ферментов при переваривании и наличие ворсинок пищеварительного эпителия при всасывании продуктов в организм;

2. На скорость реакции оказывают влияние диффузионные стадии подхода реагентов к поверхности раздела фаз: если реакция протекает на внешней поверхности раздела фаз, влияет внешняя диффузия в границах одной фазы; если реакция протекает в значительной мере внутри реакционной фазы, то добавляется внутренняя диффузия внутри её.

Катализ

Катализом называется явление ускорения реакций в присутствии веществ, которые участвуют в промежуточных взаимодействиях, но сохраняют свою химическую неизменность после протекания реакций. Такие вещества называют катализаторами, они служат основой большинства промышленных процессов и практически всех биохимических реакций. Биологические катализаторы называются ферментами. Именно химическая неизменность отличает катализаторы от уже упомянутых индукторов, которые создают реакционные пути, но в цепи реакций химически изменяется. В зависимости от того образуют частицы катализатора отдельную фазу или нет выделяют гомогенный катализ и гетерогенный.

Механизм действия катализаторов объясняется из теории промежуточных взаимодействий. Катализаторы реагируют с исходными веществами, образуя промежуточные, при распаде которых образуются конечные продукты реакции. Из уравнения Аррениуса видно, что скорость может меняться или воздействием на величину энергии активации или на предэкспоненциальный множитель:

1. Энергия активации может меняться двумя путями. Предполагается, что комплекс катализатора с реагентами, распадаясь на продукты реакции и исходный катализатор, требует для образования меньшей энергии активации, чем прямое взаимодействие реагентов (рис.6.а) или катализатор реагирует с реагентами по очереди, энергия активации каждой стадии меньше исходной и хотя суммарная энергия активации не меняется, возникает ситуация прыжка через пропасть в несколько (на рис.6.b в два) приемов, вместо одного большого кванта энергии достаточно нескольких средних. Видимая ситуация, когда реакция протекает только в присутствии катализатора может быть объяснена из термической устойчивости соединений: энергия

активации реакции без катализатора может быть настолько велика, что начинается термический распад продукта, катализатор позволяет образоваться продукту в более мягких условиях, а снижение Е_акт резко ускоряет реакцию (снижение на 40 кДж/моль ускоряет реакцию приблизительно в 2.5×10⁸ раз);

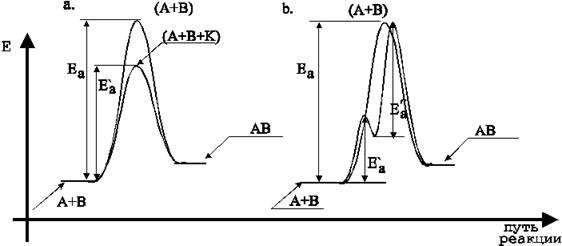
Рис.6

2. Выше упоминалось, что не все частицы, обладающие необходимой энергией, могут вступать в реакцию, значение имеет взаимная ориентация и особенности электронного распределения в реагирующих частицах; все эти факторы отражаются в предэкспоненциальном множителе. Участие катализатора позволяет оптимизировать и эти факторы: образуются комплексы с более доступными для реакции фрагментами молекул, электроны катализаторов, обладающих металлической или полупроводниковой проводимостью, могут участвовать в промежуточных стадиях с образованием реакционноспособных частиц.

Из строения биологических тканей очевидна большая распространенность в биологии явлений гомогенного катализа (реакции веществ, растворенных в тканевых жидкостях). Рассмотрим простейшие механизмы.

Все процессы пищеварения проходят в средах с определенным рН, т.е наряду с белковыми ферментами определенную роль играет кислотно- основной катализ: углеводороды расщепляются ферментами слюны при рН»6-7, жиры и белки при рН>7. По механизму специфического кислотного катализа протекает гидролиз сахарозы. Протон, контактируя с мостиковым кислородом, снижает электронную плотность на углеводных остатках и они становятся более доступными для атаки молекулой воды, после отщепления одного из сахаров, протонированная форма другого быстро отбрасывает протон и таким образом замыкает реакцию с восстановлением каталитической частицы (порядок выделения углеводов примерный, оба остатка равнодоступны).

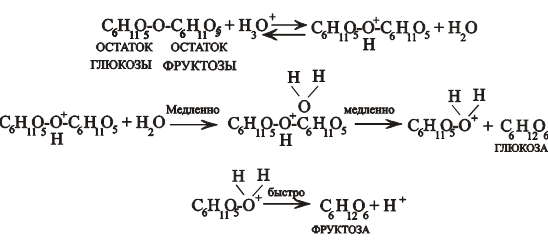
Жиры по природе своей являются сложными эфирами трехатомного спирта глицерина и различных карбоновых кислот. Их гидролиз происходит под специфическим основным катализом, рассмотрим гидролиз по первой ступени и обозначим R- радикал в такой реакции, а R₁, R₂, R₃- кислотные остатки:

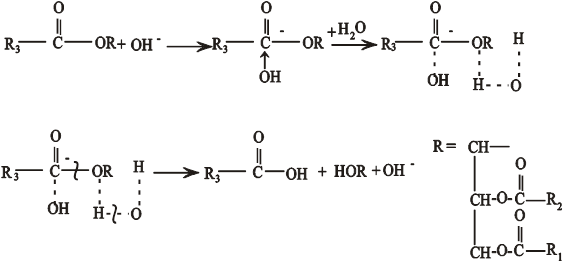
В данной реакции первой стадией становится атака гидроксильного аниона на углерод карбоксильной группы, на котором электронная плотность сильно снижена из- за соседства двух атомов кислорода, один из которых образует двойную связь; на второй стадии с молекулой жира координируется молекула воды, протон от воды подходит к сложноэфирному кислороду и отрицательный заряд от гидроксила, попадая на связи воды, вызывает их перестройку: возникает электронная плотность между протоном и эфирным кислородом, между кислородом гидроксила и углеродом карбоксильной группы, разрыхляются связи протонов с кислородом в молекуле воды (пунктир показывает промежуточный характер всех связей); завершается реакция образованием стабильных молекул кислоты, частично гидролизованного жира и гидроксильного аниона, но гидроксил возникает из атомов исходно входивших в молекулу воды, а жир может вступать в цикл реакций, вплоть до полного гидролиза до глицерина и жирных кислот.

Особенностью биологических реакций является участие в них катализаторов белковой природы- ферментов. Они позволяют протекать реакциям, обычно идущим при достаточно жестких условиях (высокие температуры, давления и т.д.) при нормальных условиях с очень высокой селективностью. Обычно для нормального протекания реакций в организмах необходимо существование сбалансированной цепочки ферментов, воздействующих на течение последовательных реакций. Для ферментов остаются верными все закономерности для макромолекул, катализаторов и поверхностно- активных веществ (ПАВ):

1. Все белки являются представителями поликонденсационных полимеров- полиамидами, они образуются из аминокислот с общей формулой R-CH(NH₂)-COOH (R- органический радикал) по реакции

nH₂N-CHR-COOH ® H₂N-CHR-CO-( -NH-CHR-CO-)_n-2-NH-CHR-COOH

где n может быть достаточно велико, а R могут быть различны ( в белках обнаружены более 20 аминокислот). В растворах полимеры имеют свойства отличающие их от растворов обычных низкомолекулярных веществ и близкие к свойствам коллоидных, где в растворителе распределены не молекулы, а агрегаты другой фазы. Кроме того, термодинамически выгодно нахождение в растворителе не линейных молекул полимера, а конформаций молекул, допускающих внутримолекулярные взаимодействие. Для белков обнаружено 4 уровня структурирования: первичный- для очень разбавленных растворов индивидуальные распрямленные молекулы, максимально взаимодействующие с растворителем; вторичный- для более концентрированных растворов начинают образовываться спиральные структуры с внутримолекулярными Ван- дер- Ваальсовскими взаимодействиями; третичный- спирали дополнительно могут сворачиваться в клубки за счет дополнительных диссперсионных взаимодействий; четвертичный- клубки могут агрегироваться между собой. Вторичная и дальнейшие структуры белков могут поддерживаться химическим связыванием между группировками, входящими в состав радикалов.

2. Вещества, способные концентрироваться на поверхности раздела фаз и менять поверхностное натяжение на границе называют поверхностно- активными. Выделяют следующие классы ПАВ: анионные- носителем свойств является гидрофобный анион, катионные- гидрофобным является катион, амфолитные (амфотерные)- в молекулу входят как анионные, так и катионные группировки и свойства ПАВ зависят от рН, неионогенные- не образуют ионов, поверхностная активность достигается чаще всего наличием в молекуле оксиэтиленовых звеньев . В молекулы белков входят аминогруппы, способные давать катионы в кислой среде и карбоксильные группы, дающие анионы в щелочной, т.е. белки являются амфо-терными ПАВ. Для каждого белка существует точка нулевого потенциала, рН при котором катионные и анионные группировки взаимоуравновешены, на этом основан метод хроматоэлек-трофоретического разделения белков.

3. Среди свойств катализаторов упоминалось наличие активных комплексов для гомогенного или активных центров для гетерогенного катализа. Все это верно и для ферментов, каждая реакция проходит на своём активном центре, если фермент полифункционален, то центров может быть несколько. Белковая природа определяет особенности функционирования ферментов: все ферменты проявляют специфическую активность только в форме третичной или чет