Суточных удоев коров хозяйства
| Классы середина (w) | Частоты f | a | fa | fa2 |
13 3 —4 —12 48
15 6 —3 --18 54
17 10 —2 —20 40
19 15 —1 —15 15
21 24 0
23 19 +1 +19 19
25 14 +2 +28 56
27 6 +3 +18 54
29 2 +4 + 8 32
31 1 +5 + 5 25
К=2 n=100 ∑fa=+13 ∑fa2=343
Подставив вычисленные величины в формулу (8)получим:
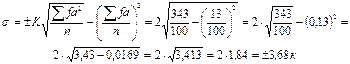
Итак, среднее квадратическое отклонение данного вариационного ряда равно ±3,68 кг молока. Сигма имеет два знака («+» и «—»), так как варианты могут отклоняться от средней арифметической как в положительную, так и в отрицательную сторону.
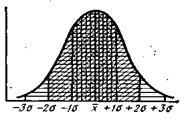 Специальные вычисления показывают, что в генеральной совокупности в пределах Х±1σ находится 68% вариант совокупности, в пределах Х±2 σ —95,5% вариант, а в пределах Х±3 σ —99,7% или практически почти все варианты (рис.8).
Специальные вычисления показывают, что в генеральной совокупности в пределах Х±1σ находится 68% вариант совокупности, в пределах Х±2 σ —95,5% вариант, а в пределах Х±3 σ —99,7% или практически почти все варианты (рис.8).
Крайние значения (лимиты) в генеральной совокупности будут находиться в пределах Х±3 σ, а в данном примере:
X+3 σ = 21,26+3х3,68 = 21,26 +11,04=32,30 кг;
X — За =  21,26— 3-3,68 =
21,26— 3-3,68 =
= 21,26—11,04= 10,22 кг.
Рис. 8. Доля вариант, откл няющихся от средней арифметической на +1σ, +2σ и +3σ (правило «плюс —минус» трех сигм.
Вычисление среднего квадратического отклонения для альтернативных признаков.
Показатель разнообразия для альтернативных признаков определяется при помощи среднего квадратического отклонения в относительных и абсолютных выражениях по формулам:
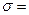
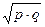 , или
, или 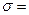
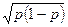 (9)
(9) 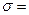
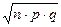 (10)
(10)
где р — доля особей, имеющих данный признак в совокупности; q — доля особей без данного признака; п — общее поголовье.
Пример. Требуется определить величину среднего квадратического отклонения по показателю наличия животных желательного типа при разведении помесных овец, полученных при скрещивании овец породы прекос с баранами породы тексель.
Из 1000 голов поголовья 650 голов было желательного, а 350 — нежелательного типа:
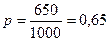
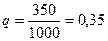
Проверка правильности расчетов проводится по формуле р+q=1. В данном примере 0,65+0,35=1. Среднее квадратическое отклонение будет равно:
σ = 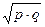 =
= 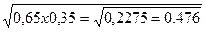 (или 47,6%);
(или 47,6%);
σ = 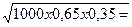
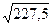 =15 гол.
=15 гол.
Вычисление коэффициента вариации (Сv). Среднее квадрэтическое отклонение — величина именованная. При изучении суточных удоев она выражается в килограммах, при изучении жирности молока — в процентах, при изучении промеров — в сантиметрах и является показателем признака для группы с определенной средней арифметической величиной. При изучении разнообразия признаков, выраженных в различных единицах измерения |(см, кг, % и др.), и при больших различиях средних арифметических величин сравниваемых групп сигма не может быть использована. В таких случаях используют другой показатель — коэффициент вариации (Cv), вычисляемый па формуле:
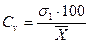 (%). (11)
(%). (11)
Пример. Требуется сравнить разнообразие различных признаков в группах по следующим показателям:
 Х σ
Х σ
Живая масса коров, кг . . . . . 500 46
Суточный удой, кг ... . 12 3
Высота в холке, см . . . . . . 130 8,5
Вычислив по формуле (11) коэффициент вариации, получаем:
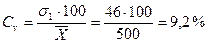
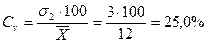
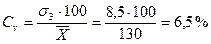
При сравнении коэффициентов вариации видно, что наибольшее разнообразие наблюдается по удою, наименьшее — по высоте в холке.
Нормированнное отклонение (t). Кроме характеристики вариационного ряда в целом по величине среднего квад-ратического отклонения, бывает необходимость оценки отдельных вариант по отношению их к средней арифметической величине совокупности. Оценка эта проводится при помощи нормированного отклонения.
Показатель нормированного отклонения определяется по разности между вариантой (х). и средней арифметической величиной (X), отнесенной к величине среднего квадратического отклонения (σ).
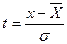
Каждая варианта характеризуется определенным значением t. Если показатель нормированного отклонения какой-либо варианты равен +1. значит, эта варианта больше X на одну сигму. Если другой вариант равен —2, то это означает, что он меньше X на две сигмы.
Нормированное отклонение используется при решении ряда вопросов (при оценке производителей по качеству потомства, при сравнении показателей животных из разных совокупностей, при оценке эффективности лечения и др.).
Показатель нормированного отклонения удобен как для оценки отдельных вариант, так и при характеристике сравниваемых групп.
Пример. При отборе сравниваются две разновозрастные коровы стада. От одной коровы за 305 дней первой лактации получено 3600 кг молока (х1 = 3600 кг), от второй за такой же период шестой лактации получено 4580 кг (х2=4580 кг). Простое сравнение их удоев для выбора лучшей коровы привело бы к ошибочному выводу. При сравнении их следует учитывать величину удоев в связи с возрастом коров и вычислить показатель нормированного отклонения. _
В стаде средний удой первотелок составляет 2500 кг (Х1= 2500), а удой коров шестого отела — Х2=3500 кг. Соответственно σ 1=500 кг, σ 2_ = 600 кг.
Нормированное отклонение для сравниваемых коров будет составлять:
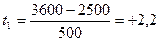
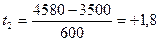
Полученная величина t для первой коровы — первотелки свидетельствует о значительном отклонении ее от средней величины удоя в группе. Можно с уверенностью сказать, что к шестому отелу она раздоится и будет более молочной, чем вторая корова.
Занятие 4. ИЗМЕРЕНИЕ СВЯЗИ МЕЖДУ ПРИЗНКАМИ
Цель занятия.Освоение методов вычисления показателей связи между признаками и приобретение навыков по использованию этих показателей в селекционной работе и прогнозировании селекции.
Методические указания. При одновременном изучении совокупности животных по нескольким признакам нередко обнаруживается, что между признаками существует взаимная связь. Например, более крупные животные имеют более высокую продуктивность. Эта взаимосвязь обнаруживается только в совокупности. У отдельных животных, при одинаковой живой массе продуктивность может значительно различаться, так как продуктивность зависит не только от размера животных, но и от многих других факторов.
Взаимная связь признаков в их изменении называется корреляцией. По форме корреляция может быть прямолинейной и криволинейной, по направлению — прямой (положительной) и обратной (отрицательной).
При прямолинейной связи равномерным изменениям одного признака соответствуют равномерные изменения второго признака при незначительных отклонениях. Например, при увеличении длины тела на 1 см ширина его тоже увеличивается на определенную величину.
При криволинейной связи с увеличением одного признака другой увеличивается до определенного момента, а затем уменьшается (или наоборот). Например, с увеличением возраста удой увеличивается до 6—7-го отела, а затем у большинства коров снижается. При криволинейной корреляции связь сначала положительная, затем отрицательная — при увеличении первого признака второй, коррелирующий с ним, уменьшается.
Степень связи между признаками измеряется при помощи коэффициентов корреляции (r), корреляционного отношения (η), тетрахорического показателя, частного и множественных коэффициентов корреляции, коэффициентов регрессии.
Изучение связи между признаками имеет большое значение при решении генетико-селекционных вопросов. Установление фенотипической и генотипической связи между признаками позволяет вести косвенную селекцию
по коррелирующим признакам и используется для прогноза селекции»
Вычисление коэффициента фенотипической корреляции (r) в малочисленных выборках. Наиболее приемлемы в биологических работах в малочисленных выборках формулы (12) и (13).
При наличии ЭВМ эти формулы используются и для многочисленных выборок.
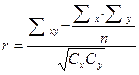 (12)
(12)
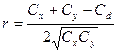 (13)
(13)
где п— число животных, изучаемых по двум признакам; х и у — значения вариант первого и второго признака; С — сумма квадратов центральных отклонений, вычисляемая по формуле:
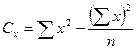 (14)
(14)
Величину С вычисляют отдельно: Сх для ряда х, Су для ряда у, Cd для ряда разностей между ними (х—у).
Техника вычисления г на примере корреляции между возрастом и плодовитостью свиноматок по данным малой выборки (л=110) приводится ниже.
В рассматриваемом примере возраст выражен порядковым номером опороса, плодовитость — числом поросят в помете (табл. 5).
