Использование метода импедансометрии в биологии и медицине.

Методы импедансометрии (измерение полного сопротивления - импеданса) находит широкое применение для изучения электрических свойств биологических объектов (клеток, тканей, органов).

При анализе электрических свойств биологических тканей необходимо учесть главную особенность их структуры - клеточное строение. Все ткани строятся из клеток (Рис. 10а), ограниченных оболочками - мембранами (1). Липидные мембраны имеют малую электропроводность, а внутриклеточная (2) и межклеточная (3) жидкости, содержащие ионы разных знаков, обладают значительно большей электропроводностью. Под действием внешнего электрического поля, созданного между электродами Э₁ и Э₂, ионы начинают упорядоченное движение. Вследствие плохой электропроводности мембран по обе стороны от них происходит накопление ионов разных знаков. Это означает, что биологические ткани обладают емкостными свойствами.

С учетом этих свойств, Фрике и Морзе предложили эквивалентную электрическую схему для биологических тканей. Эта схема содержит омическое сопротивление R, соответствующее сопротивлению межклеточной жидкости, омическое сопротивление r, соответствующее сопротивлению внутри-клеточной жидкости и конденсатор С, определяющий емкостные свойства биологической ткани.

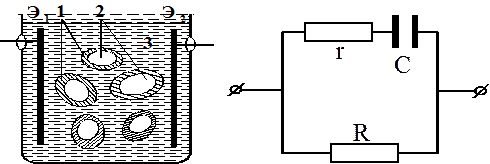А) б)

Рис. 10

Электрическая эквивалентная схема биологической ткани приведена на (рис.10б).

Полное сопротивление эквивалентной схемы, рассчитанное по методу векторных диаграмм равно

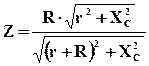(28),

График зависимости полного сопротивления Z от частоты приведен на рис.11.

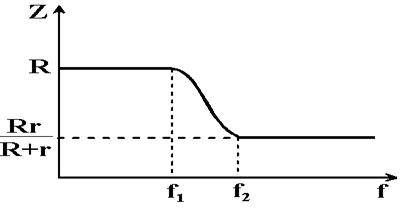
Рис. 6.11

Как видно из рис.11, полное сопротивление эквивалентной схемы на низких частотах остается практически постоянным. Это объясняется тем, что на низких частотах сопротивление конденсатора С оказывается очень большим и ток идет практически только через сопротивление R. Таким образом, сопротивление эквивалентной схемы на низких частотах равно сопротивлению межклеточной жидкости. Значит, если измерить сопротивление эквивалентной схемы на низких частота (на частотах, на которых оно остается практически постоянным), то можно определить сопротивлению межклеточной жидкости

R = Z_НЧ

Полное сопротивление эквивалентной схемы остается практически постоянным и на высоких частотах. Это объясняется тем, что на этих частотах сопротивление конденсатора С практически равно нулю. Полное сопротивление схемы определяется сопротивление параллельно соединенных сопротивлений r и R. Это сопротивление равно

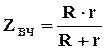(29)

Измерив полное сопротивление эквивалентной схемы на высоких частотах Z_ВЧ и зная сопротивление межклеточной жидкости R, можно найти сопротивление внутриклеточной жидкости r. Исходя из (29), оно будет равно

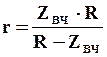(30)

В области средних частот полное сопротивление эквивалентной схемы определяется как активными сопротивлениями r и R, так и емкостным сопротивлением клеточных мембран (сопротивлением конденсатора С).

За счёт влияния ёмкостного сопротивления клеточных мембран полное сопротивление эквивалентной схемы с ростом частоты уменьшается от R (сопротивления межклеточной жидкости) до значения Z_ВЧ, определяемого формулой (29). Измерив значение Z в области средних частот (где оно уменьшается с ростом частоты) и зная сопротивления r и R, можно найти ёмкостное сопротивление клеточных мембран. Оно исходя из (28), будет равно

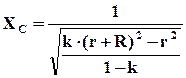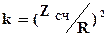, где (31)

А зная Х_С можно найти эквивалентную емкость, создаваемую клеточными мембранами.

Клеточные мембраны проявляют ёмкостные свойства лишь в живых, нормально функционирующих клетках и тканях. При отмирании тканей это свойство утрачивается и их импеданс становится чисто активным. Таким образом, наличие частотной зависимости импеданса ткани свидетельствует о её нормальном состоянии, а постоянство величины Z при изменении частоты - об отмирании ткани или её серьезных повреждениях. Эту особенность используют для оценки пригодности законсервированных органов и тканей при трансплантации (пересадке).

Контрольные вопросы по теории

1. Переменный электрический ток, его определение.

2. Синусоидальный переменный ток. Основные характеристики переменного напряжения и тока (мгновенное и амплитудное значения силы переменного тока, период, линейная частота, круговая частота, фаза).

3. Выражение для мгновенного значения синусоидального переменного напряжения, используемого потребителями.

4. Графики зависимости переменного синусоидального тока от времени и от текущей фазы (ωt).

5. Цепь с омическим сопротивлением. Мгновенные значения напряжения и силы тока в цепи с омическим сопротивлением. Действующее (эффективное) значение силы синусоидального переменного тока.

6. Сущность явления самоиндукции. Индуктивность катушки.

7. Цепь с катушкой индуктивности. Мгновенные значения напряжения и силы тока в цепи с катушкой индуктивности. Индуктивное сопротивление.

8. Конденсатор. Ёмкость конденсатора.

9. Цепь с конденсатором. Мгновенные значения напряжения и силы тока в цепи с конденсатором. Ёмкостное сопротивление.

10. Активное и реактивные (индуктивное и ёмкостное) сопротивления. Зависимость индуктивного и емкостного сопротивлений от частоты.

10. Цепь с последовательным соединением R, L, C. Векторная диаграмма токов и напряжений.

11. Закон Ома для полной цепи с R, L, C. Полное сопротивление (импеданс) цепи. Сдвиг фазы между током и напряжением.

12. Резонанс напряжений, значение полного сопротивления RLC-цепи при резонансе.

13. Метод импедансометрии в биологии и медицине.

14. Эквивалентная электрическая цепь биологического объекта.

15. График зависимости импеданса биологического объекта от частоты переменного напряжения.