Особенности расчета цилиндрических зубчатых передач

Для любой схемы (рис.4.1) двухступенчатых цилиндрических редукторов расчет следует начинать с тихоходной ступени.

5.2.1. Редуктор с раздвоенной ступенью

Наиболее рациональной и чаще встречающейся при раздвоении является

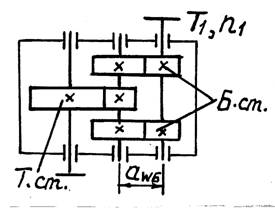
схема с раздвоенной быстроходной ступенью (рис.5.1)

Тихоходную ступень (Т.ст.) выполняют прямозубой (для разгрузки подшипников от осевых сил), косозубой, а при больших нагрузках – шевронной. Для выравнивания нагрузки по раздвоенным потокам входной вал редуктора должен быть ²плавающим², а при шевронной Т.ст.–два ²плавающих² вала: входной и промежуточный. При расчете параметров быстроходной раздвоенной ступени коэффициенты yba и ybd выбирают из табл.4.1 для каждой (одной) половины раздвоенной ступени:

Рис. 5.1. Схема редуктора Ц2РБ

при Н₂ < 350 НВ y_ba = 0,16…0,25;

при Н₁ и Н₂ >350 НВ y_ba = 0,16…0,2.

Это необходимо при определении K_Hb⁰ по табл.4.5.

При расчете a_WБ по формуле (5.1) y_ba (а при расчете d_W1Б по формуле (5.2) y_bd ) удваивается, так как обе половины ступени передают момент Т₁:

a_WБ ¢ = 410 (u +1) Ö T₁K_H / (2y_baus_HP²) (5.13)

Рабочая ширина каждой половины b_W¢ = y_ba a_WБ , (5.14)

где a_WБ после округления.

В случае раздвоения тихоходной ступени (применяется редко) все сказанное здесь имеет место и для нее.

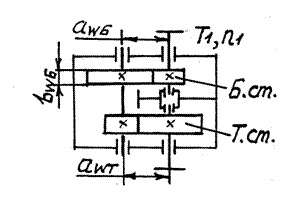
5.2.2. Соосный редуктор

Рис.5.2. Схема редуктора Ц2С

Для соосных редукторов (рис.5.2) расчетом определяется aWТ¢ более нагруженной тихоходной ступени. По условиям компоновки принимают aWБ = aWТ = aW . После этого находят рабочую ширину венца bWБ =ybaБ aW быстроходной ступени, где ybaБ¢= Ka3(uБ ± 1)3T1БКНБ / (uБaW3sHPБ2) ³ 0,16 (5.15) (индекс ²Б² указывает, что параметры принимаются для быстроходной ступе-ни)

Величина y_baБ¢ округляется в большую сторону по ряду чисел:

0,16; 0,18; 0,2; 0,224; 0,25; 0,315; 0,355; 0,4; 0,45; 0,5.

Если при расчете получилось y_ba¢< 0,16, то следует принять y_ba¢= 0,16.

5.2.3. Прямозубые колеса применяют при невысоких окружных скоростях, в открытых, планетарных и реечных передачах, в коробках скоростей при необходимости осевого перемещения колес для переключении скорости.

5.2.4. Несмотря на то, что основным критерием работоспособности открытых и высокотвердых (Н > 56 HRC_Э) закрытых передач является сопротивление зубьев изгибной усталости и, строго говоря, их проектировочный расчет следовало бы начинать с определения модуля по напряжениям изгиба s_F, однако в настоящее время их расчет выполняют по общей методике для зубчатых передач, т.е. начинают его с определения a_W или d_W1 по контактным напряжениям. При этом рекомендуют принимать большие значения модуля (по сравнению с менее твердыми закрытыми передачами), а также применять положительное смещение х₁ у шестерни, что повышает изгибную прочность зубьев.

5.2.5. Для планетарных передач во всех формулах проектировочного и проверочного расчетов к расчетному моменту Т вводится сомножитель K_C/n_C, где K_C – коэффициент, учитывающий неравномерность распределения нагрузки между сателлитами:

K_C = 1,1…1,2 – при наличии устройств для выравнивания нагрузки по сателлитам;

K_C = 1,6…2 – при отсутствии выравнивания нагрузки ;

n_C – число сателлитов.

Коэффициент y_bd принимают равным :

для улучшенных колес 0,7…0,5;

для закаленных колес 0,5…0,3.

Рассматривая планетарную передачу как соосную, достаточно рассчитать a_W или d_W1 пары с внешним зацеплением (центральная шестерня – сателлит). При этом коэффициент K_Hb определяется по формуле (4.6), где K_Hb⁰ выбирается из табл. 4.5 для консольной схемы 1 (рис.4.1).

В приложении (табл.П1) приведены формулы для определения передаточных отношений и КПД типовых схем планетарных передач.

5.2.6. При расчете прямозубой реечной передачи:

d_W1¢ = 770 [ T₁ K_Hb/ (y_bds_HP²) ]^1/3 , (5.14)

где y_bd = 0,4…0,6 (0,8) – меньшие значения при консольном расположении шестерни.

Коэффициент K_Hb находят по формуле (4.6), где K_Hb⁰ принимают для консольных схем 1 или 2 (рис.4.1) из табл. 4.5.

5.2.7. Межосевое расстояние коробки скоростей следует определять:

при Т₂ – const по зубчатой паре с наибольшем u;

при Т₂ – var по зубчатой паре с наибольшим Т₂.