Особенности расчета конических колес

В конической передаче (рис. 3.2) оси валов обычно пересекаются под углом 90⁰. В этом случае передаточное число равно [13]:

u = n₁ / n₂ = z₂ / z₁ = tgδ₂ = ctgδ₁,

где δ₁ и δ₂ – половины углов при вершинах начальных конусов, δ₁+ δ₂=90⁰.

Максимальное передаточное число конической передачи равно 6,3., рекомендуемое – 2…3.

Для конических передач основным расчетным параметром является внешний делительный диаметр колеса d_e2:

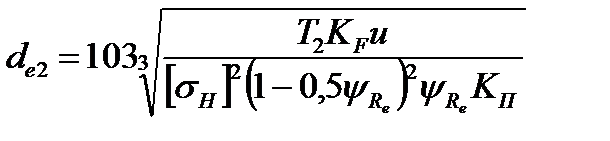
где ψ_Re = b / R_e– коэффициент длины зуба, К_П – коэффициент, учитывающий повышение нагрузочной способности косозубых передач по сравнению с прямозубыми.

Рекомендуется [13] выбирать ψ_Re =0,25-0,3, а также b<0,3R_e и b<10m_e.

Для прямозубых колес К_П = 1, для колес с наклонными и круговыми зубьями К_П = 1,15-1,35.

Расчетные значения внешнего делительного диаметра колеса должны округляться в большую сторону по ряду чисел [13]: 50, 63, 80, 100, 125, 160, 200, 250, 280, 315, 355, 400, 450, 500, 560, 630, 710, 800, 900, 1000, 1250, 1400, 1600.

Для обеспечения выполнения геометрических и технологических условий изготовления конических передач количество зубьев шестерни вычисляется по следующей формуле, которая носит рекомендательный характер:

.

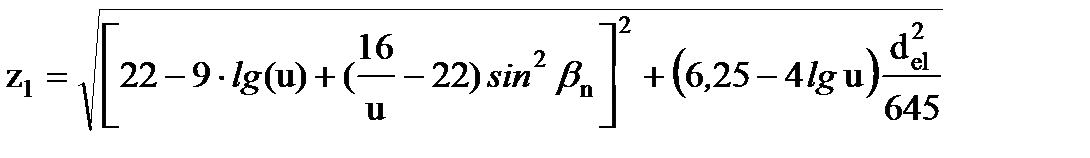В случае прямозубых конических передач полученная расчетом величина z₁ не должна быть меньше 20. В противном случае принимают

z₁ = 20.

Расчеты конических передач проводятся по размерам, связанным с большими основаниями конусов.

Основными параметрами конической передачи являются: внешние делительные диаметры d_e1 и d_e2, внешний окружной модуль m_e , длина образующей делительного конуса R_e (внешнее конусное расстояние).

d_e1 = m_e z₁, d_e2 = = m_e z₂

R_e1

d_e1 δ₁

δ₂ b

d_a1

d₂

d_a2

Рис. 4.2 Элементы конической передачи

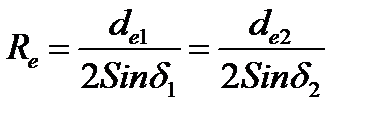
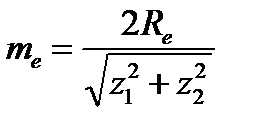
Диаметры окружностей конусов вершин зубьев:

d_a1 = d_e1 + 2m_eCos δ₁

d_a2 = d_e2 + 2m_eCos δ₂

Диаметры окружностей конусов впадин:

d_f1 = d_e1 – 2,5m_eCos δ₁

d_f2 = d_e2 – 2,5m_eCos δ₂

Средние делительные диаметры:

d₁ = 2(R_e-0,5b)Sin δ₁

d₂ = 2(R_e-0,5b)Sin δ₂

Модуль в среднем сечении (средний окружной модуль) равен: m = d₁ / z₁ = d₂ / z₂

Проверка контактной прочности зубьев конических колес проводится по соотношению [13]:

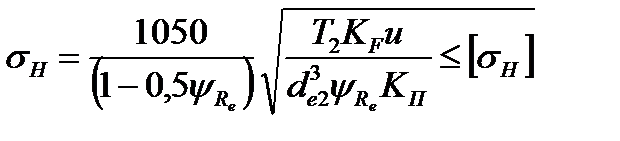
Напряжения изгиба в зубьях конических косозубых колес должны удовлетворять условию [1]:

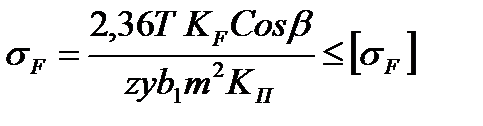
В этом выражении у – коэффициент формы зуба конического колеса, определяемый по приведенному значению числа зубьев, которое определяется из выражений [1]:

При прямых зубьях z_np1 = z₁ / Cosδ₁ и z_np2 = z₂ / Cosδ₂

При наклонных и круговых зубьях z_np1 = z₁ / Cosδ₁Cos³β и z_np2 = z₂ / Cosδ₂Cos³β.

Таблица 4.10 Коэффициент формы зуба у [1]

z, znp
у	0,384	0,395	0,404	0,412	0,417	0,426	0,435	0,442	0,446	0,452	0,458	0,471	0,48	0,482	0,496

Таблица 4.11 Ширина зубчатых венцов конических колес b[1]

de2 мм	Ширина зубчатого венца b в зависимости от передаточного числа u
1,4	1,6	1,8	2,0	2,24	2,5	2,8	3,15	3,55	4,0	4,5	5,0	5,6	6,3
		8,5	-	-	-	-	-	-	-	-	-	-	-	-
		9,5	-	-	-	-	-	-	-	-	-	-	-	-
		10,5			-	-	-	-	-	-	-	-	-	-
			11,5	11,5	-	-	-	-	-	-	-	-	-	-
							-	-	-	-	-	-	-	-
							-	-	-	-	-	-	-	-
									-	-	-	-	-	-
									-	-	-	-	-	-
											-	-	-	-
												-	-	-