Расчет зубьев на выносливость при изгибе

Силы, действующие в зацеплении:

· окружная F_t = 2T₁ / d₁ = 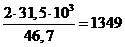Н;

· радиальная F_r = F_t tg a / cos b = 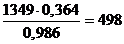Н;

· осевая F_a = F_t tg b = 1349×0,176 = 237 Н.

Проверяем зубья на выносливость по напряжениям изгиба по формуле

s_F = F_t K_F Y_F Y_b K_FL / (b m_n) < s_FР.

Коэффициент нагрузки

K_F = K_Fb K_FV,

где K_Fb – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (коэффициент концентрации нагрузки), K_Fb = 1,33 (табл. П.3.12);

K_FV – коэффициент, учитывающий динамическое действие нагрузки (коэффициент динамичности), K_FV = 1,3 (табл. П.3.13).

Таким образом

K_F = K_Fb K_FV = 1,33×1,3 = 1,73;

Y_F – коэффициент, учитывающий форму зуба, определяем по эквивалентному числу зубьев Z_V:

Z_V1 = Z₁/ cos³ b = ;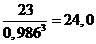

Z_V2 = Z₂/ cos³ b = .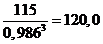

Y_F1 = 3,98 (табл. П.3.14);

Y_F2 = 3,6 (табл. П.3.14);

Y_b – коэффициент учитывающий угол наклона зубьев;

K_FL – коэффициент долговечности, зависящий от соотношения базового и эквивалентного числа циклов.

K_FL = ,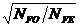

где N_FE – эквивалентное число циклов напряжений.

Базовое число циклов по ГОСТ N_FO = 4×10⁶; при эквивалентном числе циклов большем базового (что принято при курсовом проектировании), K_FL = 1.

Допускаемые напряжения на изгиб

s_FP = s°_{F lim b} K_FL K_FC / S_F,

где S_F = S_F¢ S_F¢¢,

здесь S_F – коэффициент безопасности,

S_F¢ – коэффициент, учитывающий нестабильность материала зубчатых колес, S_F¢ = 1,75 (табл. П.3.15);

S_F¢¢ – коэффициент, учитывающий способ получения заготовки для изготовления зубчатого колеса, для поковок и штамповок S_F¢¢ = 1,0.

Таким образом, S_F = 1,75 ×1 = 1,75.

K_FC – коэффициент, учитывающий влияние двухстороннего приложения нагрузки. При одностороннем приложении нагрузки K_FC = 1, при двухстороннем – K_FC = 1- g_FC (коэффициент, учитывающий влияние химико-термической обработки, табл. П.3.15).

s°_{F lim b1} = 1,8 НВ (табл. П.3.15);

s°_{F lim b1} = 1,8 НВ = 1,8 ×230 = 414 МПа (для шестерни);

s°_{F lim b2} = 1,8 × 200 = 360 Мпа (для колеса).

Допускаемые напряжения:

· для шестерни s_FР1 = 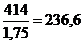МПа;

· для колеса s_FР2 = 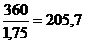МПа.

Находим отношения s_FР1 / Y_F1:

· для шестерни s_FР1 / Y_F1 = 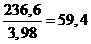МПа;

· для колеса s_FР2 / Y_F2 = 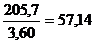МПа.

Вывод: дальше расчет производим только для колеса, так как соотношение s_FР1 / Y_F1 > s_FР2 / Y_F2 для колеса меньше, чем для шестерни.

Определим коэффициенты:

Y_b = 1- b / 140 = .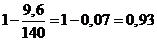

Для средних значений торцевого перекрытия x_a =1,5 и 8-й степени точности K_Fa= 0,92, n – степень точности колес, n = 8.

Проверяем прочность зуба по формуле

s_F = F_t K_F Y_F Y_b K_Fa / (bm_n)= 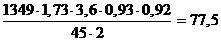МПа < s_FР2 =206 МПа.

Условие прочности при изгибе зубьев выполнено.

Предварительный расчет валов редуктора

Расчет ведущего вала

Диаметр выходного конца вала

d_в1 = [16Т₁ / (p[t_к] )]^1/3,

где [t_к] – допустимые касательные напряжения при кручении.

[t_к] = 20 … 25 МПа.

d_в1 = 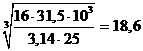мм.

Принимаем ближайшее значение из стандартного ряда (табл. П.3.24) d_в2 = 18 мм.

Диаметр вала под подшипниками d_п2 = 20 мм (табл. П.3.16). Диаметры остальных участков вала назначаем из конструктивных соображений с учетом рекомендаций табл. П.3.24 и П.3.25.

Из технологических соображений целесообразно вал и шестерню выполнять в виде отдельных деталей, но в данном случае мы будем иметь слишком тонкую стенку между внутренним диаметром шестерни и шпоночным пазом. Если перемычка меньше 10 мм, целесообразно выполнять вал-шестерню.

В нашем случае (d_f – d_в) / 2 = (41,7 – 25) / 2 = 8,35 < 10 мм, поэтому шестерню выполним за одно целое с валом. Конструкция ведущего вала приведена на рис. 3.

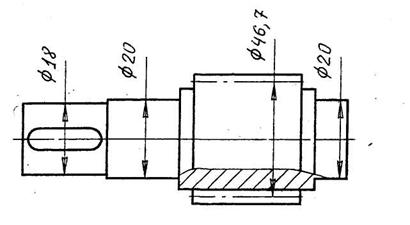Рис. 3. Конструкция ведущего вала
3.2. Расчет ведомого вала

Учитывая влияние изгиба вала от натяжения цепи, при расчете ведомого вала примем [t_к]=20 МПа.

Диаметр выходного конца вала:

d_в2= [(16Т₂ / (p[t_к])]^1/3 = 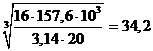мм.

Принимаем ближайшее значение из стандартного ряда (табл. П.3.24) d_в2=30 мм.

Высота буртов вала принимается в соответствии с табл. П.3.25. Диаметр вала под подшипниками d_п2=35 мм (табл. П.3.16), под зубчатым колесом d_к2=40 мм.

Диаметры остальных участков вала назначаем из конструктивных соображений с учетом рекомендаций табл. П.3.24, П.3.25. Конструкция ведомого вала приведена на рис. 4.

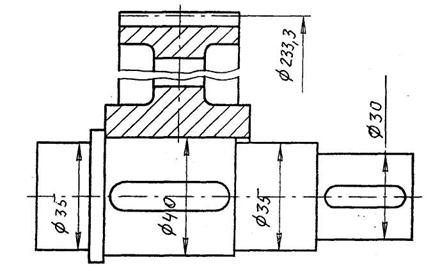Рис. 4. Конструкция ведомого вала