Расчет червячной передачи по напряжениям изгиба
Для прямозубых зубчатых колёс условие прочности по изгибным напряжениям

 Для червячного колеса (рис. 10.6)
Для червячного колеса (рис. 10.6)


где 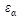 и
и  - учитывают наличие перекрытия и реальную длину линии контакта;
- учитывают наличие перекрытия и реальную длину линии контакта;

 .
.
Тогда условие прочности для червячного колеса запишется
 ,
,
где Yb=cos2gw – коэффициент, учитывающий отличия в работе биэквивалентного прямозубого колеса и реального червячного колеса, или

Для средних приведенных значений d=500;ea=1,6; ku= 0,75 получим

Для проектировочного расчета модуль определяют по зависимости m=d2/z2.
Здесь d2 принимают из проектировочного расчета на контактную выносливость, а z2= z1U, где z1 – число заходов.
Тепловой расчет червячного редуктора
Механическая энергия, затрачиваемая на преодоление сил трения в червячном редукторе, превращается в тепло. Повышение температуры приводит к снижению вязкости в смазке и её защитных свойств, что приводит к вероятности задиров. Условие теплового расчета tm £ [tm], где [tm] = 80…95 0C, для авиационных масел [tm] =110 0C – допускаемая температура масла.
Мощность теплового потока выделяемого в результате работы сил трения
 .
.
Мощность, отводимая в результате охлаждения определяется по зависимости
 .
.
Здесь kT=12…19 Вт/м2·С0– коэффициент теплоотдачи от поверхности корпуса редуктора; А – поверхность охлаждения, [м2]; (tm-t0) – разность температур масла и окружающего воздуха [0C] , где t0=20 0С.
Таким образом, в связи с наличием трения тепло подводится, а из-за теплоотдачи отводится. С течением времени установится постоянная температура вследствие теплового баланса, т.к. Pr=Pотв . Следовательно можно записать
1000P1(1-h)=kTA(tm-t0).
Из последнего уравнения находят
 .
.
Если оказалось, что tm> [tm], то используют следующие мероприятия:
- Снижают потери на трение;
- Увеличивают поверхность охлаждения за счет оребрения;
- Применяют искусственное охлаждение – обдув, водяное охлаждение масляной ванны, циркуляционная смазка. За счет этого kT можно увеличить в 10 и более раз.
Лекция №11
Ременные передачи
 Элементы геометрии ременной передачи
Элементы геометрии ременной передачи
Ременная передача состоит из ведущего и ведомого шкивов, соединенных ремнем. Ремни бывают плоские, клиновидные и круглые (рис. 11.1). Нагрузка передается силами трения между шкивом и ремнем. При геометрическом расчете обычно известны d1 и d2 – диаметры шкивов и межосевое расстояние а. Определяется угол охвата ремнем малого шкива α через угол между ветвями ремня β и длину ремня l. Вследствие вытяжки и провисания ремня, величины α и l не являются строгими и определяются приближенно. Из рис.11.1 видно, что α=1800-β. Проведем из О1 линии параллельно ремню. Они отсекут на диаметре d2 окружность d2 - d1. Из ∆О1О2В видно, что  так как
так как  , то
, то  т.е.
т.е.
 ;
;  .
.

 Длина ремня определяется как сумма прямолинейных участков и дуг охвата
Длина ремня определяется как сумма прямолинейных участков и дуг охвата
Используя ряд Макларена для  , можно записать
, можно записать


Скольжение в ременной передаче

Исследования Н.Е. Жуковского показали, что в ременных передачах следует различать два вида скольжения ремня по шкиву - упругое скольжение и буксование. Природа упругого скольжения может быть установлена из следующего опыта. Пусть ремень расположен на заторможенном шкиве (рис. 11.2). В начале опыта к концам ремня подвешены равные грузы F. Под действием грузов между ремнем и шкивом возникает сила трения, затем левая часть ветви догружается грузом F1. Если сила F1 будет больше сил трения между ремнем и шкивом, то равновесие нарушится и ремень соскользнет со шкива. Под дополнительным грузом ремень растянется на дуге l1. Длина дуги зависит от F1 и силы трения на этом участке. Дополнительное упругое удлинение ремня будет сопровождаться его скольжением по шкиву. Это скольжение принято называть упругим, а дугу l1 – дугой упругого скольжения. Дуга l2 называется дугой покоя.
При увеличении силы F1 до значения, равного запасу сил трения (l2=0) равновесие нарушится и начнется буксование.
 В реальной передаче (рис 11.3) роль грузов F выполняет сила натяжения ведомой ветви F2, а роль дополнительного груза F1 – окружная сила Ft. Здесь F0 – предварительное натяжение ремня. Разность натяжения ведомой и ведущей ветви, создаваемая нагрузкой, вызывает упругое скольжение. При этом дуги упругого скольжения расположены по разные стороны сбегающей ветви.
В реальной передаче (рис 11.3) роль грузов F выполняет сила натяжения ведомой ветви F2, а роль дополнительного груза F1 – окружная сила Ft. Здесь F0 – предварительное натяжение ремня. Разность натяжения ведомой и ведущей ветви, создаваемая нагрузкой, вызывает упругое скольжение. При этом дуги упругого скольжения расположены по разные стороны сбегающей ветви.
Передаточное число ременной передачи
Выделим некоторый участок ремня длиной l в ненагруженной передаче, а затем дадим нагрузку. При прохождении ведущей ветви отмеченный участок удлинится l+∆, а ведомой сократится l-∆, тогда окружные скорости будут
 и
и  ,
,
где t - время прохождения участка. Значит скорость V2<V1.

где  - коэффициент скольжения.
- коэффициент скольжения.
Тогда V2=V1(1-e).
Окружные скорости
 ;
;  .
.
Отношение  тогда
тогда  .
.
По мере роста нагрузки увеличивается ∆, а значит, возрастает разность окружных скоростей и меняется передаточное отношение. Упругое скольжение является причиной некоторого непостоянства передаточного отношения в ременной передаче. При перегрузке дуга покоя уменьшается до 0, ремень начинает скользить по всей поверхности шкива, наступает режим буксования. При этом ведомый шкив останавливается, а КПД передачи равен 0.


 Силы в ременной передаче
Силы в ременной передаче
Рассмотрим два случая (рис. 11.4). В первом случае (рис. 11.4, а) нагрузка отсутствует (Т1=0). Здесь F0 – предварительное натяжение ремня. Во втором случае (Рис. 11.4, б) передача нагружена моментом Т1>0. Здесь F1 и F2 – натяжение ведущей и ведомой ветвей. Окружная сила  .
.
По условию равновесия шкива имеем
 или
или  (11.1).
(11.1).
Связь между F0, F1 и F2 можно установить на основе следующих рассуждений. Геометрическая длина ремня не зависит от нагрузки и остается неизменной как в ненагруженной, так и в нагруженной передаче. Следовательно, дополнительная вытяжка ведущей ветви компенсируется сокращением ведомой. Согласно закону Гука деформация пропорциональна силе, тогда запишем
F1=F0+∆F, F2=F0 - ∆F или F1+F2 =2F0. (11.2).
Из совместного решения уравнений (11.1)и(11.2) получим
 ,
,  .
.
Последние уравнения устанавливают изменение натяжения ведущей и ведомой ветвей в зависимости от нагрузки Ft и предварительного натяжения F0, но не вскрывают тяговой способности передачи, которая связана с величиной сил трения между ремнем и шкивом. Эта связь установлена Л. Эйлером. Он установил зависимость между F1 и F2 на границе буксования, то есть определил максимально допустимую величину Ft в зависимости от F0 при условии использования полного запаса сил трения.
 ;
;  ;
;  ;
;  , здесь f - коэффициент трения.
, здесь f - коэффициент трения.
При круговом движении ремня со скоростью V на каждый его элемент массой dm, расположенный в пределах угла охвата, действуют элементарные центробежные силы dFc (рис 11.5). Действие этих сил вызывает дополнительное натяжение Fv во всех сечениях ремня.
 ,
,
где g - удельный вес ремня, g - ускорение силы тяжести, b - ширина, d - толщина ремня.
 Из условия равновесия ремня получим
Из условия равновесия ремня получим  .
. 

Натяжение Fv ослабляет полезное действие предварительного натяжения F0. Оно уменьшает величину сил трения и тем самым понижает нагрузочную способность передачи.
Нагрузка на валы и опоры
Силы натяжения ветвей ремня (за исключением FV) передаются на валы и опоры (рис.11.6). Равнодействующая нагрузка определяется как
 .
.
 Равнодействующая R в 2…3 раза больше окружной силы Ft.
Равнодействующая R в 2…3 раза больше окружной силы Ft.
Основные преимущества ременной передачи:
1. Возможность передачи момента между валами, расположенными на значительном расстоянии;
2. Плавность и бесшумность работы;
3. Предохранение механизмов от перегрузок вследствие проскальзывания;
4. Малая стоимость.
Основные недостатки ременной передачи:
1. Большие габариты;
2. Непостоянство передаточного числа вследствие проскальзывания;
3. Повышенные нагрузки на валы из-за натяжения ремня;
4. Малая долговечность;
Напряжения в ремне
Наибольшие напряжения действуют в ведущей ветви ремня (рис 11.7):
1)  ,
,
где  - полезное напряжение;
- полезное напряжение;  - напряжение от предварительного натяжения;
- напряжение от предварительного натяжения;  - площадь поперечного сечения ремня;
- площадь поперечного сечения ремня;
2)  - напряжение от центробежных сил;
- напряжение от центробежных сил;
3) sи-изгибные напряжения, возникают в той части ремня, которая огибает шкив.
Согласно закону Гука изгибные напряжения определяются в виде
sи = Ee.
Здесь E – модуль упругости материала ремня;
 - относительное удлинение нагруженных волокон ремня при чистом изгибе,
- относительное удлинение нагруженных волокон ремня при чистом изгибе,
где y– расстояние от нейтрального слоя, r– радиус кривизны нейтрального слоя.
Для ремня, огибающего шкив  ,
,  ,
,  , тогда
, тогда
 .
.
Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив  .
.
 Эпюра распределения напряжений по длине ремня имеет вид, показанный на рис. 11.7.
Эпюра распределения напряжений по длине ремня имеет вид, показанный на рис. 11.7.
Критерии работоспособности ременных передач
Основные критерии работоспособности:
1) тяговая способность;
2) прочность;
3) усталостная долговечность.
Виды разрушений ремня:
1) буксование ремня сопровождается разогревом и износом;
2) усталостное разрушение ремня – разрыв за счет накопления усталости;
3) статическое разрушение – разрыв ремня.
Согласно формулам Эйлера, необходимое натяжение ремня
 , отсюда
, отсюда  .
.
Отношение  называется коэффициентом тяги, тогда
называется коэффициентом тяги, тогда  - критический коэффициент тяги.
- критический коэффициент тяги.
Если j =j0, то ремень начинает буксовать. Это выражение теоретическое, а на практике j0 определяют опытным путем. Так как j и e ~ Ft, то e ~ j.
 В настоящее время работоспособность ременной передачи характеризуют кривыми скольжения e = f(j) и КПД h = f(j) (рис.11.8). Также кривые являются результатом испытаний ремней различных типов. По оси ординат отложено относительное скольжение e и КПД, а по оси абсцисс – нагрузка передачи, которую выражают через коэффициент тяги j. На начальном участке кривой скольжения от 0 до j0 наблюдается только упругое скольжение. Дальнейшее увеличение нагрузки приводит к частичному, а затем и полному буксованию. Рабочую нагрузку рекомендуется выбирать вблизи критического значения j0 слева от него. Этому значению соответствует и максимальное значение h = 0,96…0,97. Долговечность ремня зависит не только от величины напряжений, но и от характера и частоты цикла изменения этих напряжений.
В настоящее время работоспособность ременной передачи характеризуют кривыми скольжения e = f(j) и КПД h = f(j) (рис.11.8). Также кривые являются результатом испытаний ремней различных типов. По оси ординат отложено относительное скольжение e и КПД, а по оси абсцисс – нагрузка передачи, которую выражают через коэффициент тяги j. На начальном участке кривой скольжения от 0 до j0 наблюдается только упругое скольжение. Дальнейшее увеличение нагрузки приводит к частичному, а затем и полному буксованию. Рабочую нагрузку рекомендуется выбирать вблизи критического значения j0 слева от него. Этому значению соответствует и максимальное значение h = 0,96…0,97. Долговечность ремня зависит не только от величины напряжений, но и от характера и частоты цикла изменения этих напряжений.
Из рис.11.9 видно, что напряжения в ремне изменяются по пульсирующему знакопеременному циклу, что приводит к усталостному разрушению ремня. Частота цикла напряжений равна частоте пробегов ремня:
 ,
,
где V – окружная скорость, l – длина ремня.
Чем выше частота lП, тем меньше долговечность ремня, поэтому введены ограничения на частоту пробегов ремня lП=3…5 для плоских ремней и lП=10…20 для клиновидных ремней. Кроме того с увеличением lП увеличивается температура ремня. Это также приводит к снижению прочности.
|
Лекция №12
Валы и оси
Все детали, совершающие вращательное движение, вращаются вокруг некоторых геометрических осей. На практике эти геометрические оси воплощаются в реальные детали – валы и оси.
Оси предназначены для поддержания вращающихся деталей и обеспечения их геометрической оси вращения. Они могут быть как вращающимися, так и неподвижными и воспринимают только напряжение изгиба.
Валы, в отличие от осей, предназначены, кроме перечисленных функций, и для передачи крутящих моментов от одной детали к другой и испытывают напряжения изгиба и кручения. Валы и оси вращаются относительно опор, называемых подшипниками. Различают валы прямые, коленчатые и гибкие. Наибольшее распространение имеют прямые валы. Коленчатые валы применяют в поршневых машинах. Гибкие валы допускают передачу вращения при больших перегибах оси.
По конструкции различают валы и оси, гладкие и фасонные. По виду поперечного сечения валы и оси могут быть сплошными и полыми. Применение пустотелых валов позволяет существенно снизить их вес при сохранении равной прочности и жесткости вала.
Изучить самостоятельно: конструкции осей и валов; материалы для изготовления осей и валов.

 Рис. 11.9
Рис. 11.9