Какие виды резьбы применяют для гаек в передаче винт-гайка?
4.6.Силовые соотношения в винтовой паре передачи.
Для удобства рассмотрения сил в винтовой паре развернем виток резьбы по среднему диаметру d2 в наклонную плоскость, а гайку представим в виде ползуна (рис. 4.9).
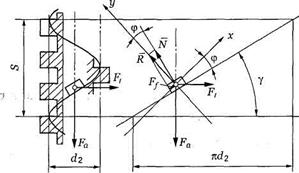
Рис. 4.9. Силовые соотношения в винтовой передаче
Силы, возникающие в резьбе: Fa — осевая сила; F, — окружная сила (F, = 2T/d2; Ff=fN, где f — коэффициент трения; N — нормальная реакция).
На рис. 4.9 R — равнодействующая сил Nw Ff, угол ср между, векторами сил R и N — угол трения. Из теоретической механики известно, что/= tgc. Зависимост^между^ и Ft найдем из уравнения равновесия гайки под действием сил Fn Fa, R:
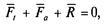
откуда получим соотношение модулей сил
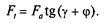 (4.1)
(4.1)
Формула (4.1) справедлива только для прямоугольной резьбы. Для треугольной или трапецеидальной резьбы
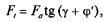 (4.2)
(4.2)
где φ' = arctg(f/cosα/2) — приведенный угол трения; a — угол профиля резьбы.
Уточните, как осуществляется преобразование вращательного движения в поступательное.
4.7. Самоторможение в передаче винт-гайка.
В этом случае под действием силы Fa гайка не может поворачиваться (из-за трения) относительно неподвижного винта. Условие самоторможения
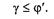 (4.3)
(4.3)
По условию (4.3) проверяют, например, винтовые домкраты (см. рис. 4.2). Груз не должен опускаться, пока к рукоятке не приложена сила Резьбы многозаходные для передачи движения (специальные) имеют уго.-подъема винтовой линии резьбы у = 8-^16°, угол трения ф = 2 -=- 6° (для стального винта и бронзовой гайки) и ф = 4 -ь 8° (для стального винта и чугунной гайки).
Формула (4.3) определяет условие самоторможения, а именно для самоторможения передачи винт-гайка необходимо, чтобы угол подъема винтовой линии резьбы (у) был меньше приведенного угла трения ср'.
Определение угла ср':
φ = arctgf— угол трения;
 приведенный угол трения (см. шаг 4.6).
приведенный угол трения (см. шаг 4.6).
4.8.КПД винтовой пары определяют отношением
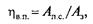 (4.4)
(4.4)
где Апс — работа сил полезного сопротивления на винте; А3 — работа движущих сил, затраченная на один оборот винта (гайки).
По известной осевой силе Fa и окружной силе F, определяют Апс и А3 (см. рис. 4.9):
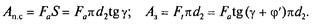
Следовательно, КПД винтовой пары
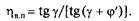 (4.5)
(4.5)
КПД можно определить и графическим путем. Для случая самоторможения (у < ф')Кпри подъеме груза КПД получается менее 50 %.
По графику (рис.4.10) определите КПД передачи винт-гайка, если у = 10°, коэффициент трения f= 0,10.
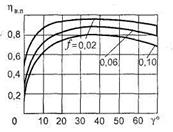
Рис. 4,10. Зависимость КПД винтовой передачи от угла подъема винтовой линии
4.9.Передаточное число передачи винт-гайка условно можно записать
u=C/S, (4.6)
где С = πD — длина окружности маховичка, с помощью которого осуществляется вращение винта (рис. 4.11); S — ход винта.
Зависимость между окружной силой на маховичке и осевой силой F:
F= FMur]Bn,
где ηBП = 0,15 ÷0,8 при коэффициенте трения f= 0,10;
ηВП = 0,20 ÷ 0,9 при f=0,06;
ηb, = 0,5 ÷ 0,97 при f=0,02.
Определить передаточное число и, если диаметр маховичка D = 300 мм, ход винта S = 1 мм.
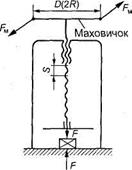
Рис. 4.11.Кинематическая схема передачи винт-гайка
4.10.Достоинства и недостатки передачи винт-гайка.
Основные достоинства: возможность получения большого выигрыша в силе; высокая точность перемещения; плавность и бесшумность работы; большая несущая способность при малых габаритных размерах; прбстота конструкции.
Недостатки передач винт-гайка: большие потери на трение и низкий КПД; затруднительность применения при больших частотах вращения.
