Построение эпюры углов закручивания

Проектировочный расчет на прочность ступенчатого стержня.

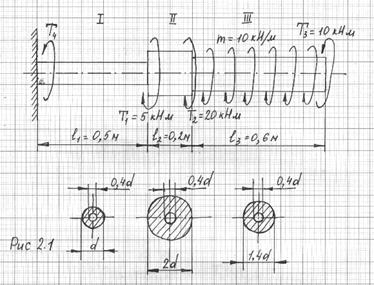
Для ступенчатого стержня, представленного на рис 2.1, необходимо построить эпюру крутящих моментов, эпюру условных касательных напряжений как функцию параметра сечения d, из условия прочности найти искомое значение d, в расчетах использовать материал, представленный кривой деформирования.

Построение эпюры крутящих моментов.

Направим вдоль оси стержня ось z (рис 2.2,а). Запишем условие равновесия стержня AD в виде:

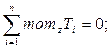
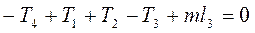
Из условия равновесия

находим значение Т₄:

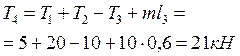
Для определения внутренних

силовых факторов, воспользуемся

методом сечений.

Разобьем стержень на три участка АВ, ВС, СD, проведем на каждом из них произвольные сечения и зададим координаты этих сечений z₁, z₂, z₃.

Рассмотрим участок АВ (0 ≤ z₁ ≤ l₁ = 0,5 м)

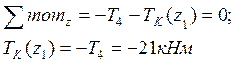
Рассмотрим участок ВС (0 ≤ z₂ ≤ l₂ = 0,2 м)

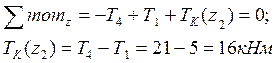
Рассмотрим участок СD (0 ≤ z₃ ≤ l₃ = 0,6 м)

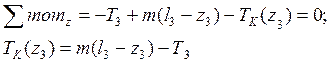
Рассчитаем значение крутящего момента в точках С и D. В точке С:

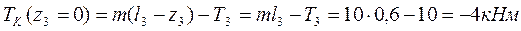
В точке D: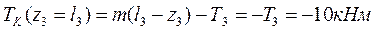

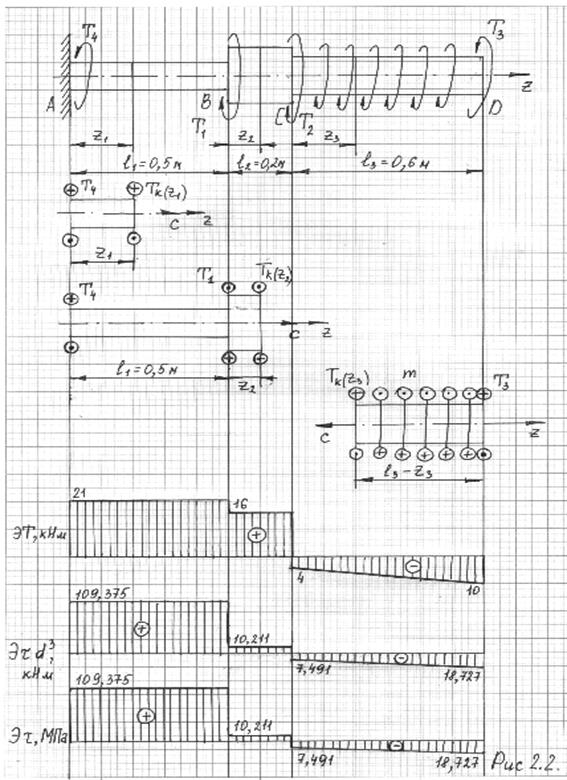
По полученным данным построим эпюру крутящих моментов (рис 2.2).

2.1.2. Построение эпюры напряжений.

Наибольшие напряжения при кручении возникают на внешних волокнах и определяются как

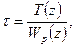
где W_p(z)= 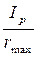- полярный момент сопротивления, I_p – полярный момент инер-ции, r_max – максимальный радиус. Определим геометрические характеристики се-чений.

Участок АВ

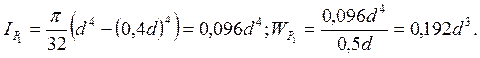
Участок ВС

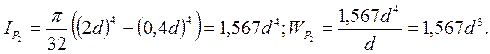
Участок CD

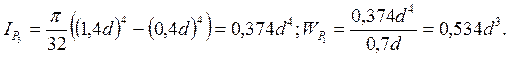
Определим опасное сечение стержня, в котором возникают максимальные напряжения, в долях 1/d³.

Участок АВ (0 ≤ z₁ ≤ l₁ = 0,5 м)

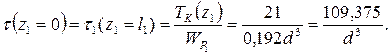
Участок ВС (0 ≤ z₂ ≤ l₂ = 0,2 м)

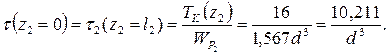
Участок СD (0 ≤ z₃ ≤ l₃ = 0,6 м)

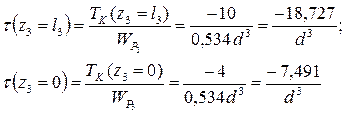
По полученным данным строим Эτ d³ (рис 2.2).

Расчет на прочность. Подбор сечения.

Из эпюры Эτ d³ видно, что опасными являются сечения на участке АВ, где дей-ствует наибольшее напряжение

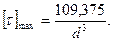
Условие прочности при кручении имеет вид:

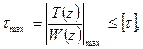где [τ] – допускаемое касательное напряжение.

Примем для материала Д16 [τ] = 0,5 [σ] = 0,5∙ 225,6 = 112,8 МПа.

Тогда условие прочности примет вид:

.

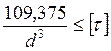Из условия прочности находим оптимальное значение диаметра:

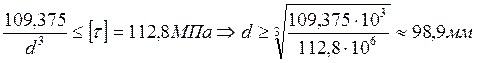
Полученное значение диаметра округляем и принимаем (из ряда Ra 40 по ГОСТ 6636-86) d = 100 мм.

Определим напряжения, действующие в сечениях при выбранном значении d.

Участок АВ:

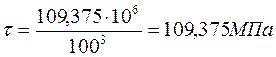
Участок ВС:

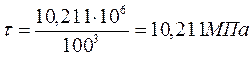
Участок CD:

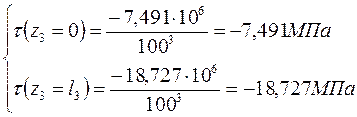
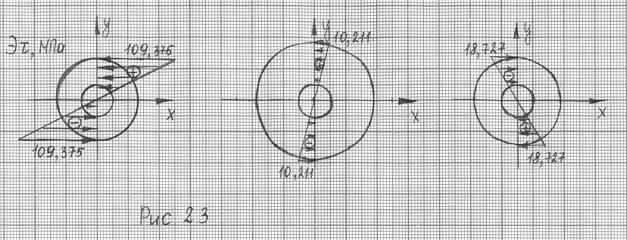
По полученным данным строим эпюру действующих на валу касательных напряжений Эτ (рис 2.2).

2.2. Расчет на жесткость стержня постоянного сечения.

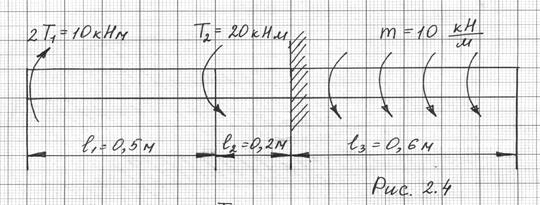
Для стержня постоянного сечения (рис. 2.4), необходимо построить эпюру углов закручивания и из условия жесткости найти искомое значение диаметра стержня d. Материал стержня – дюраль Д16.

G = 27 ГПа.

Построение эпюры углов закручивания.

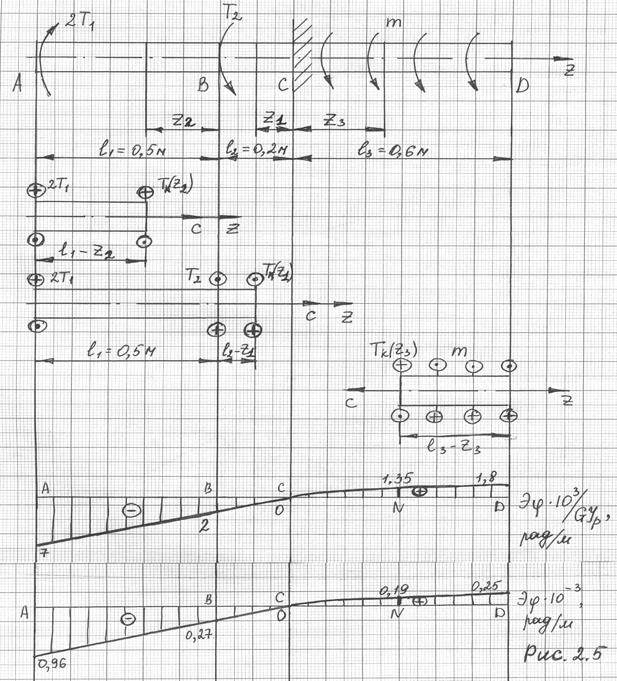
Разобьем стержень на участки АВ, ВС и СD (рис. 2.5). В пределах каждого участка возьмем произвольные сечения z₁, z₂, z₃ соответственно.

На участке ВС (0 ≤ z₁ ≤ l₂ = 0,2 м)

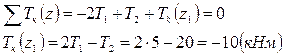
На участке АВ (0 ≤ z₂ ≤ l₁ = 0,5 м)

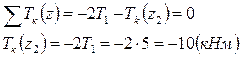
На участке CD (0 ≤ z₃ ≤ l₃ = 0,6 м)

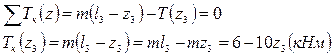
Находим углы закручивания в долях 1/GI_p.

На участке ВС (0 ≤ z₁ ≤ l₂ = 0,2 м)

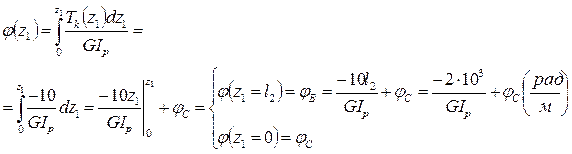
На участке АВ (0 ≤ z₂ ≤ l₁ = 0,5 м)

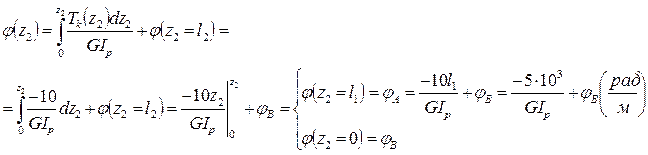
Наличие заделки в точке С говорит о том, что 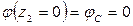, тогд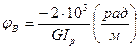а , а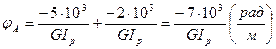

На участке CD (0 ≤ z₃ ≤ l₃ = 0,6 м)

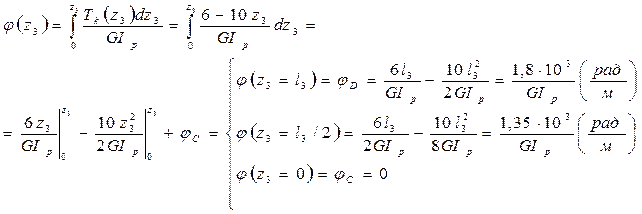
Функцией угла закручивания на участке CD является парабола.

По полученным данным значениям строим эпюру углов закручивания Эφ в долях от GI_p (рис. 2.5).

Расчет на жесткость.

По условию жесткости, максимальный угол поворота не должен превышать допускаемый [Θ] = 0,001 рад/м, т.е. φ_max ≤ [Θ]. Из эпюры углов поворота построенной в долях от GI_p , видно, что максимальный угол поворота находится в сечении А φ_max = .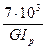

Полярный момент сечения I_p = 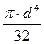, откуда найдем диаметр стержня .

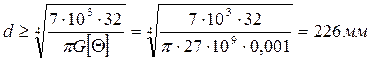Полученное значение диаметра округлим и примем (из ряда Ra 40 по ГОСТ 6636-86) d = 230 мм, тогда I_p= .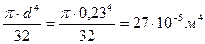

Окончательно рассчитывая углы поворота в каждом сечении, получаем

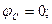
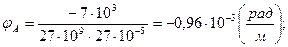
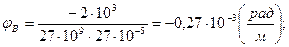
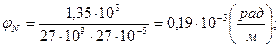
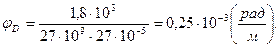
3. РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ БАЛОК И РАМ.