Алгебраические критерии устойчивости

Определение корней характеристического уравнения А(р)=0 обычно приводит к большим трудозатратам, а иногда и просто невозможно, если нет цифровых ЭВМ с соответствующими программами для нахождения этих корней. Поэтому чаще пытаются оценить устойчивость объектов косвенными алгебраическими методами, используя коэффициенты его характеристического уравнения. Среди алгебраических способов анализа устойчивости наиболее распространен метод Гурвица.

Исходная информация для использования этого метода заключена в коэффициентах характеристического уравнения объекта, устойчивость которого необходимо определить. Это уравнение записывается в следующей стандартной форме

a₀⋅pⁿ + a₁⋅p^n–1 +…+ a_n–1⋅p + a_n =0.

Далее из коэффициентов a_i, i = 0,..n составляется матрица Гурвица

Формируется она следующим образом: в диагональ сверху вниз записываются последовательно коэффициенты а₁, а₂, ...,а_n. Затем от любого члена диагонали вдоль строки вправо записываются коэффициенты с возрастанием на каждом шаге их номера на две единицы. Если коэффициент с таким номером отсутствует, то вместо него записывается нуль.

Так как математической основой критерия является теория определителей, то далее находится главный определитель Гурвица Δn и его диагональные миноры Δ_i, i=1,2,..n-1:

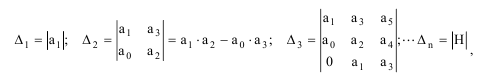
Исходя из правила Саррюса:

Δ_n = а_n ⋅ Δ_n–1

Гурвиц доказал, что если при а₀>0 положительны все n определителей Δi, i=1,2,..n, то объект является устойчивым. Если хотя бы один определитель отрицателен, то объект неустойчив.

Частный случай. Критерий И.А. Вышнеградского.

В 1876 году профессором Вышнеградским был сформулирован критерий устойчивости для системы с характеристическим уравнением третьего порядка:

если произведение параметров

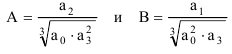
больше единицы: А⋅В >1 при А>0 и В>0, то система третьего порядка устойчива;

если А⋅В<1 при А>0 и В>0, то система третьего порядка неустойчива;

граница колебательной устойчивости системы третьего порядка определяется уравнением А⋅В = 1 при А > 0 и В > 0.

Подставив в переменные А и В значения коэффициентов а₁, а₂, а₃,

получим такое же неравенство а₁⋅а₂>а₀⋅а₃, что и по критерию Гурвица.

Таким образом, система третьего порядка устойчива, если:

а) а₀>0 ; а₁>0; а₂>0; а₃>0;

б) а₁ а₂> а₀ а₃.

Проверим разомкнутую и замкнутую системы автоматического управления по алгебраическому критерию устойчивости Гурвица- Вышнеградского.

Характеристическое уравнение разомкнутой системы:

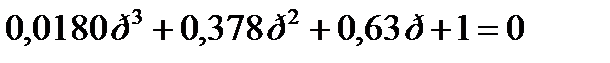
а) а₀ = 0,0108 >0 ; а₁ = 0,378 > 0; а₂ = 0,63 > 0; а₃ = 1 > 0

б) а₁ а₂> а₀ а₃; а₁ а₂ = 0,378⋅0,63=0,24; а₀ а₃ = 0,0108⋅1=0,0108, таким образом условие а₁ а₂> а₀ а₃ выполнено, т.к. 0,24 > 0,0108.

Следовательно в соответствием с критерием устойчивости Гурвица- Вышнеградского разомкнутая система автоматического управления устойчива.

Характеристическое уравнение замкнутой системы:

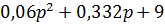
а) а₀ = 0,06 >0 ; а₁ = 0,332> 0; а₂ = 9 > 0;

б) а₁ а₂> а₀ ; а₁ а₂ = 0,332*9=2,98; а₀=0,06, таким образом условие а₁ а₂> а₀ выполнено, т.к. 2,98 > 0,06.

Следовательно в соответствием с критерием устойчивости Гурвица- Вышнеградского замкнутая система автоматического управления устойчива.

Критерий Рауса.

Как и критерий Гурвица, этот критерий представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой системы (Соломенцев). Он представляет собой некоторое правило (алгоритм), которое наиболее просто пояснять таблицей.

В первой строке таблицы записывают коэффициенты характеристического уравнения, имеющие четный индекс (а₀, а₂, а₄, ...), а во второй строке – коэффициенты характеристического уравнения с нечетными индексами (а₁, а₃, а₅, ...).

В последующие строки вписывают коэффициенты а_{k, i} = а_{k+1, i–2} – r_i а_{k+1, i–1} , где r_i = а_{1, i–2} / а_{1, i–1} ; i – индекс, означающий номер строки таблицы; k – индекс, обозначающий номер столбца таблицы. Число строк таблицы Рауса равно степени характеристического уравнения +1, т. е. (n + 1). После заполнения таблицы по ней можно судить об устойчивости системы.

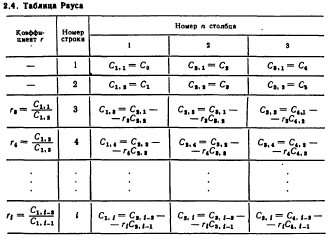
Условия устойчивости Рауса: чтобы САУ была устойчивой, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак, т. е. были бы положительными, так как всегда можно сделать а₀ > 0: а_1,1 = а₀ > 0, а_1,2 = а₁ > 0, а_1,3 > 0, …, а_{1, n + 1} > 0. Если не все коэффициенты первого столбца положительны, т. е. если система неустойчива, то число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса.

Характеристическое уравнение в общем виде:

a₀⋅pⁿ + a₁⋅p^n–1 +…+ a_n–1⋅p + a_n =0

Составляем таблица Рауса для разомкнутой системы

Таблица Рауса для разомкнутой системы

Характеристическое уравнение разомкнутой системы:

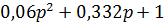
Таблица 3.

Таблица Рауса для разомкнутой системы

Коэффициент r	Номер строки	Номер n столбца
		а1,1 = а0 =0,06	а2,1 =а2=1
		а1,2 = а1 =0,332	а2,2 =а3 =0
r3= а1,1 /а1,2 =0,06/0,332=0,18		а1,3 = а2,1 – r3 а2,2 =1-0,18*0=1	а2,3 = а3,1 – r3 а3,2 =0

Разомкнутая система САУ устойчива, т.к. коэффициенты первого столбца таблицы Рауса имеют один и тот же знак, т. е. положительны.