Построение желаемой ЛАЧХ
Желаемую ЛАЧХ построим на основании требований, предъявляемых к свойствам системы по методу В.В. Солодовникова.
Желаемую ЛАЧХ условно разделяют на три части: низкочастотную, среднечастотную и высокочастотную.
Среднечастотная асимптота определяет устойчивость, запас устойчивости, быстродействие системы. Ее параметрами являются частота среза 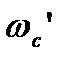 , наклон, выражаемый в децибелах на декаду и диапазон частот.
, наклон, выражаемый в децибелах на декаду и диапазон частот.
Частоту среза 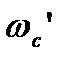 ,запасы устойчивости по модулю
,запасы устойчивости по модулю 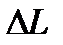 и по фазе выбирают по заданным значениям максимального перерегулирования
и по фазе выбирают по заданным значениям максимального перерегулирования 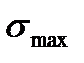 и времени регулирования
и времени регулирования 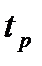 . в соответствии с номограммами предложенными Солодовниковым В.В. 5.24, 5.25, с.272 [3].
. в соответствии с номограммами предложенными Солодовниковым В.В. 5.24, 5.25, с.272 [3].
Выбираем 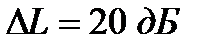 ,
, 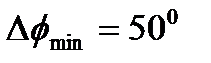 ,
, 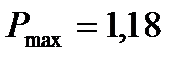 .
.
Выбираем частоту среза согласно формуле:
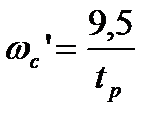 =5,9
=5,9
Отмечают ее на оси частот на том же рисунке, где изображена ЛАЧХ исходной системы (рисунок 6). Через точку 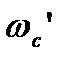 проведем прямую линию с наклоном
проведем прямую линию с наклоном 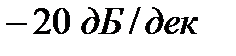 .
.
На оси ординат отметим точки с координатами 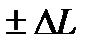 , через которые проведем пунктиром горизонтальные прямые до пересечения их с линией
, через которые проведем пунктиром горизонтальные прямые до пересечения их с линией 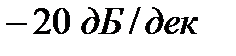 .
.
Частоты, которым соответствуют точки пересечения прямых определяют нижнюю и верхнюю границы среднечастотного диапазона (на рисунке 9 это 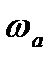 и
и 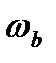 ).
).
Среднечастотную асимптоту желаемой ЛАЧХ сопрягаем с низкочастотной и высокочастотной асимптотами.
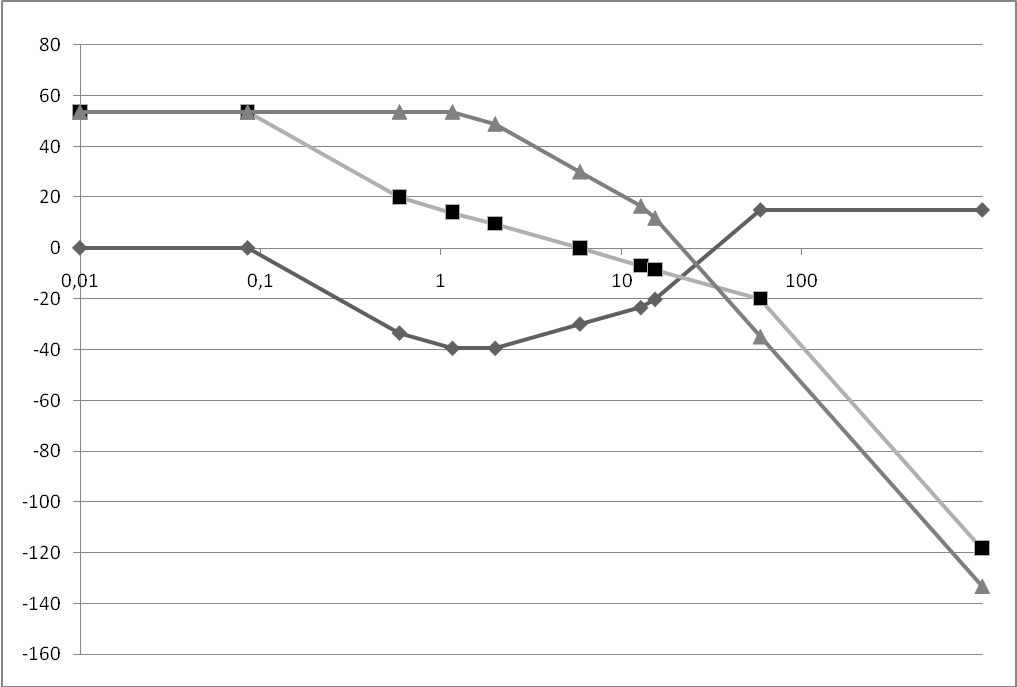 Рисунок 6 ‑ Построение желаемой ЛАЧХ и ЛАЧХ корректирующего устройства
Рисунок 6 ‑ Построение желаемой ЛАЧХ и ЛАЧХ корректирующего устройства
Проверка запаса устойчивости по фазе скорректированной системы
Проверяем запас устойчивости по фазе для желаемой ЛАЧХ.
Для этого сначала получим выражение для фазовой частотной характеристики ФЧХ системы 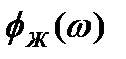 по виду желаемой ЛАЧХ.
по виду желаемой ЛАЧХ.
Фиксируем частоты излома желаемой ЛАЧХ 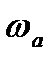 =0,59,
=0,59, 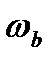 =59,
=59, 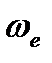 =0,085.
=0,085.
Постоянные времени найдем по формулам:
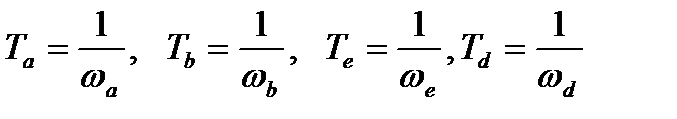 .
.
Тогда выражение для расчета фазовой частотной характеристики системы представится в виде:
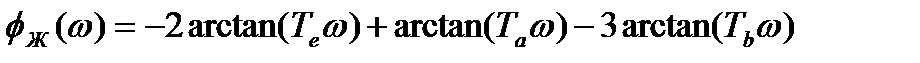 ;
;
Запас устойчивости:
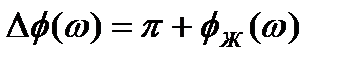 ;
;
Подставляя в данную формулу значения частот излома желаемой ЛАЧХ, получим 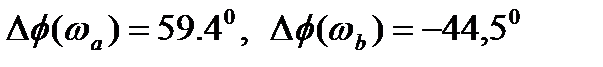 .
.
Откуда видно, что условие запаса устойчивости:
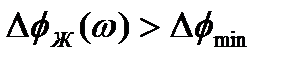
выполняется только для частоты 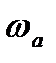 .
.
Тогда проверим выполнение данного условия на частоте среза 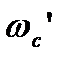 .
.
Подставив численные значения, получим 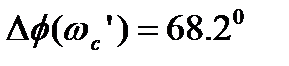 и
и 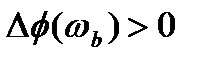 , условие выполняется, значит, вопрос о коррекции желаемой ЛАЧХ, решаем на основе оценки качества системы.
, условие выполняется, значит, вопрос о коррекции желаемой ЛАЧХ, решаем на основе оценки качества системы.
Передаточная функция разомкнутой скорректированной системы
Звенья, которые входят в скорректированную систему, определяем, как и при составлении фазовой частотной характеристики (п.2.3), по изменению наклона ЛАЧХ.
Тогда передаточная функция разомкнутой скорректированной системы представится в виде:
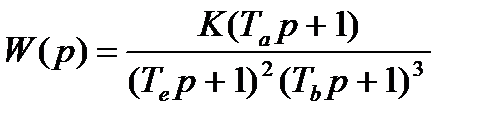 ;
;
или введя новые переменные:
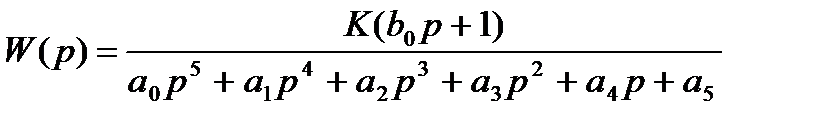 ;
;
Подставив численные значения, получим:
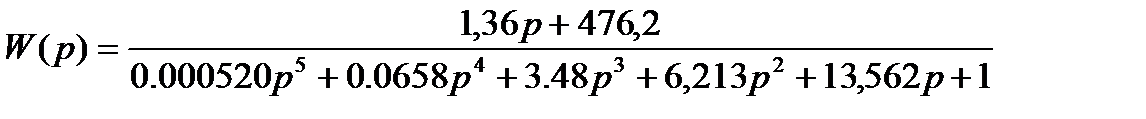 .
.
