Построим ЛАФЧХ разомкнутой системы

Содержание

Оглавление

Содержание. 2

Вариант задания. 3

Решение. 3

Структурная схема. 3

Дифференциальная схема. 3

Уравнение, описывающие процессы в объекте управления в векторно-матричной форме: 4

Функциональная схема системы с пропорциональным регулятором и заданным объектом управления, охваченного единичной обратной связью: 5

Определим передаточные функции разомкнутой системы 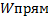, 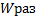и замкнутой системы 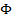по входному воздействию, 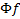возмущению и 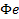ошибке: 6

Построение ЛАФЧХ разомкнутой системы.. 7

Определение частоты среза и критической частоты разомкнутой системы, полосы пропускания системы, запаса устойчивости по фазе или амплитуде: 8

Определение низкочастотной, среднечастотной и высокочастотной областей: 8

Рассчёт по косвенным оценкам качества предполагаемые значения времени регулирования, перерегулирования и статической ошибки в исследуемой замкнутой системе: 9

Оценка статическую точность замкнутой системы при отсутствии и действии возмущения: 10

Методом моделирования построение переходного процесса в замкнутой системе: 10

Заключение. 11

Список литературы.. 12

Вариант задания

Задание является индивидуальным, каждый студент получает свой вариант задания. В данном случае вариант представляет собой четырёхзначный номер: 314-5.

Для данного варианта задания таблица значений имеет вид:

Вариант	K1	K2	K3	Ta	β
				0,2	0,4

Решение

Для данного варианта структурная схема будет иметь вид:

f(t)

z(t)

y(t)

ε(t)

X(t)

U(t)

A(t)

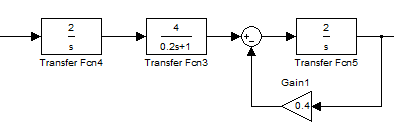
Она включает в себя 3 звена:

· Интегрирующее звено: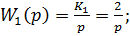

· Апериодическое звено: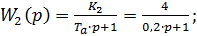

· Интегрирующее звено, охваченное отрицательной обратной связью с коэффициентом β: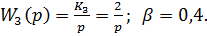

Найдём

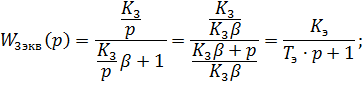
Где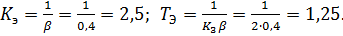

Запишем дифференциальные уравнения, описывающие процессы в объекте управления:

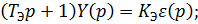
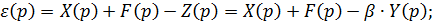
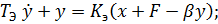
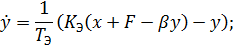
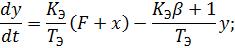
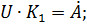
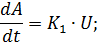
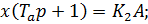
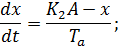
Составим систему дифференциальных уравнений:

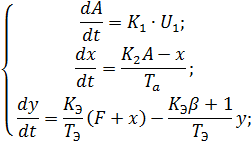
Запишем уравнения, описывающие процессы в объекте управления в векторно-матричной форме:

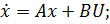
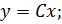
Заменим A, x, y, U₁, F:

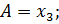
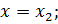
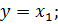
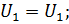
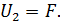
Получим следующую систему:

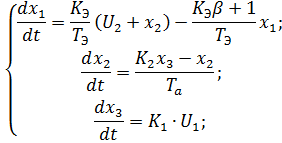
Далее определим матрицы A, B и C:

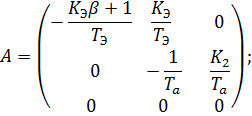
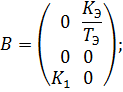
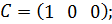
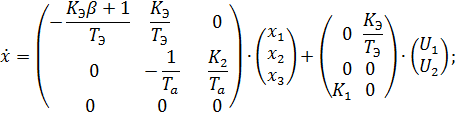
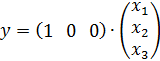
Построим функциональную схему системы с пропорциональным регулятором и заданным объектом управления, охваченного единичной обратной связью:

x(t)

f(t)

ε(t)

y(t)

А(t)

U(t)

ε2(t)

1. Анализируя полученную схему можно сделать вывод, что в данной системе используется принцип управления по отклонению.

2. Рассчитаем коэффициент усиления пропорционального регулятора:

Для начала запишем передаточную функцию системы:

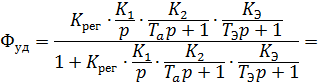
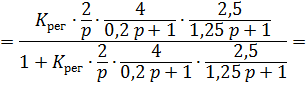
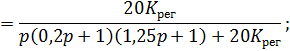
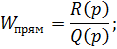
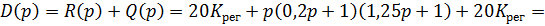
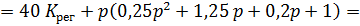
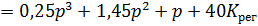
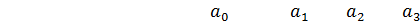
Cоставим определитель Гурвица:

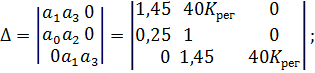
Согласно частотному случаю критерия Гурвица – критерию Вышнеградского — для устойчивости системы третьего порядка необходимо и достаточно выполнения условия: 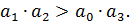Отсюда следует:

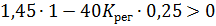
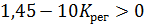
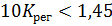
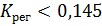
Для устойчивости системы выберем .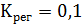

Определим передаточные функции разомкнутой системы 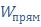, 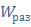и замкнутой системы 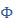по входному воздействию, 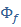возмущению и 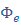ошибке:

;

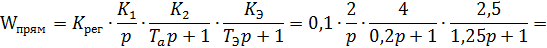
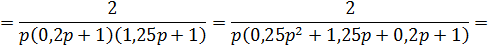
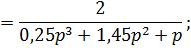
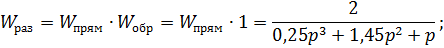
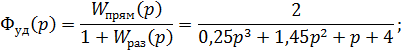
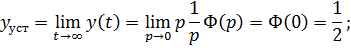
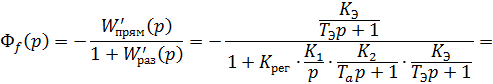
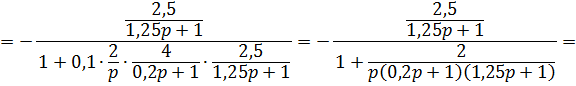
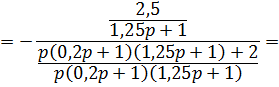
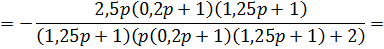
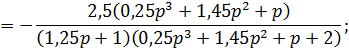
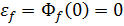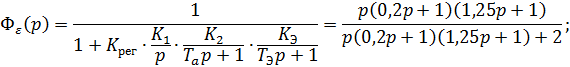
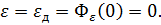
Построим ЛАФЧХ разомкнутой системы

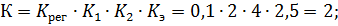
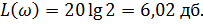
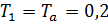
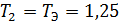
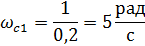
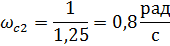
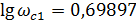
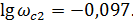
Определим частоту среза и критическую частоту разомкнутой системы, полосу пропускания системы, запасы устойчивости по фазе или амплитуде:

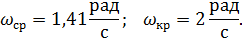
Полоса пропускания определяется по уровню -3дб. Тогда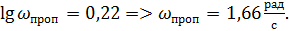

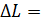9,25 дб;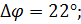

Так как разница мала, мы можем взять реальную ЛАФЧХ, построенную в MatLab для расчётов:

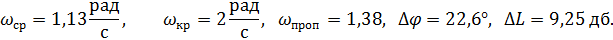
Определим низкочастотную, среднечастотную и высокочастотную области:

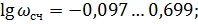
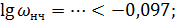
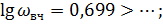
Оценим воспроизведение системы входного гармонического сигнала для выбранных значений низкой, средней и высокой частоты:

Для Низкочастотной области:

;

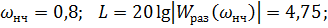
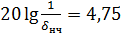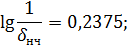
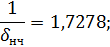
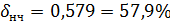
Для Среднечастотной области:

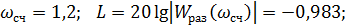
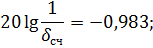
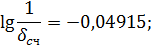
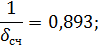
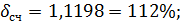
Для Высокочастотной области:

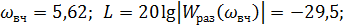
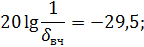
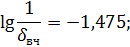
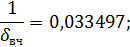
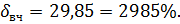
Рассчитаем по косвенным оценкам качества предполагаемые значения времени регулирования, перерегулирования и статической ошибки в исследуемой замкнутой системе:

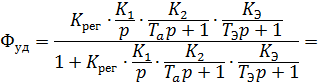
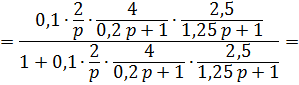
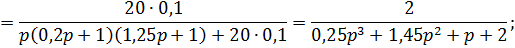
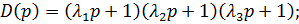
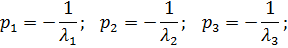
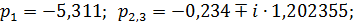=> Система устойчива.

Так как к 0 ближе располагается комплексно-сопряжённые корни в системе будет наблюдаться колебательный процесс.

Статическая ошибка:

;

;

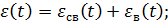
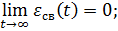
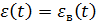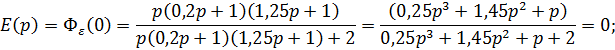
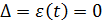Система обладает астатизмом. Следовательно, статическая ошибка равна 0.

Оценим статическую точность замкнутой системы при отсутствии и действии возмущения:

Время регулирования:

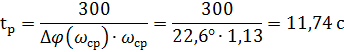
Перерегулирование:

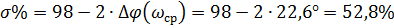
Методом моделирования построим переходный процесс в замкнутой системе:

Структурная схема с учётом действия внешнего возмущения

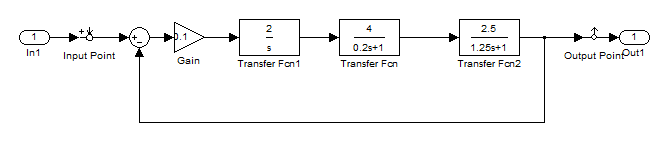
Структурная схема без действия внешнего возмущения

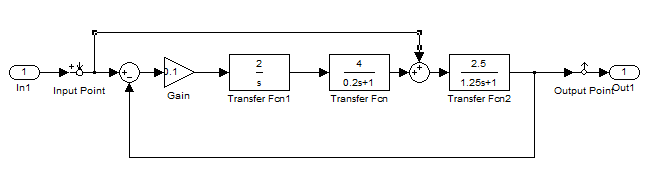Время регулирования по переходному процессу из MatLab:

При отсутствии возмущения:

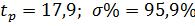
При действии возмущения:

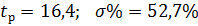
Так как полученные данные сходятся с данными ЛАФЧХ построенной в MatLab. Следовательно, расчёты произведены верно.

Заключение

При выполнении данной курсовой работы закрепляются на практике теоретические знания методов и принципов анализа, проектирования линейных систем автоматического управления, а также методик исследования и проектирования систем регулирования и автоматики.

Список литературы

1. Теория систем автоматического управления / В.А. Бесекерский, Е. П. Попов. – [Издание 4-е, переработанное и дополненное]. – СПб.:Профессия, 2004. – 752 с.

2. Теория автоматического управления: Учебник для студентов вузов, обучающихся по направлениям «Автоматизация и управление», Системный анализ и управление» / А.А. Ерофеев. – 2-е издание, дополненное и переработанное – СПб.: Политехника, 2003 – 302 с.

3. Теория автоматического регулирования: Учебное пособие для студентов вузов, обучающихся по направлению «Автоматизация и управление» / А.С. Востриков, Г.А. Французова. – М.: Высшая школа, 2004. – 365 с.

Приложение Б

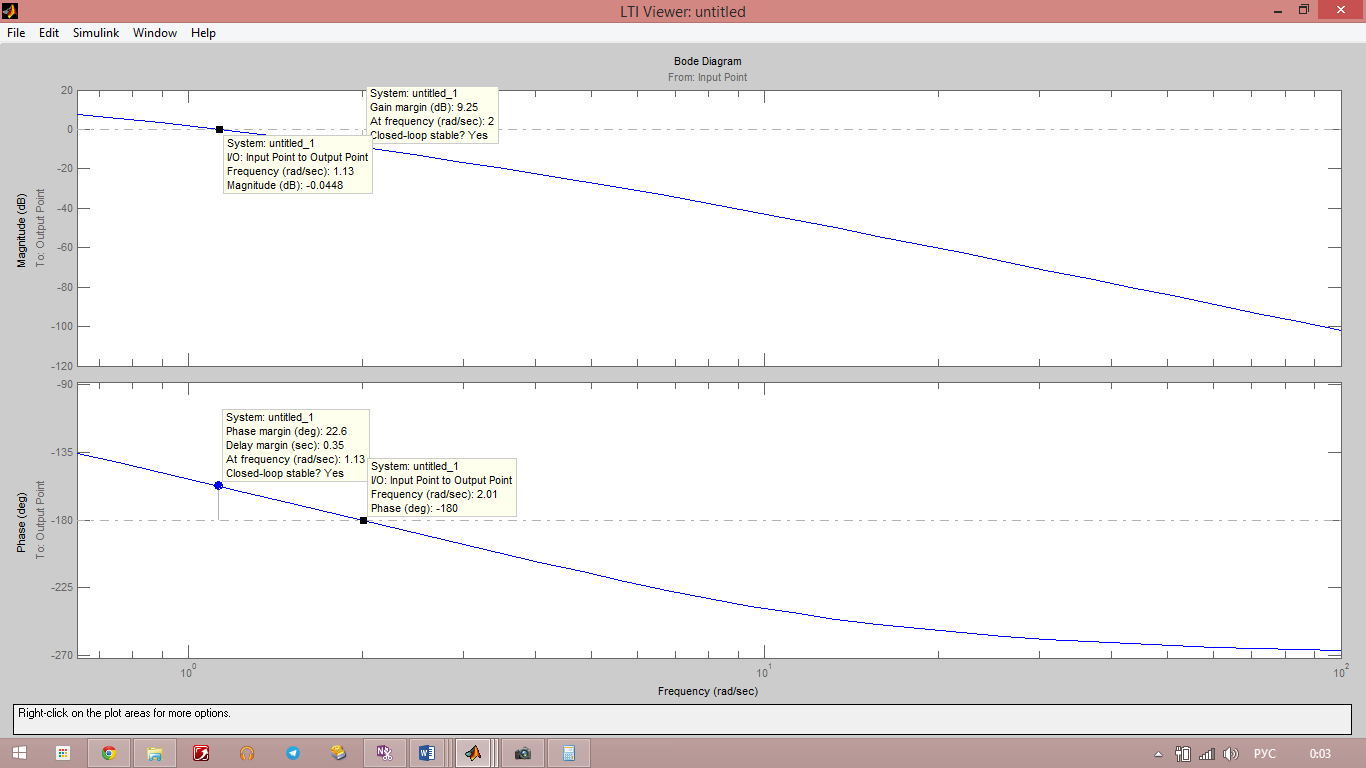
ЛАФЧХ разомкнутой системы

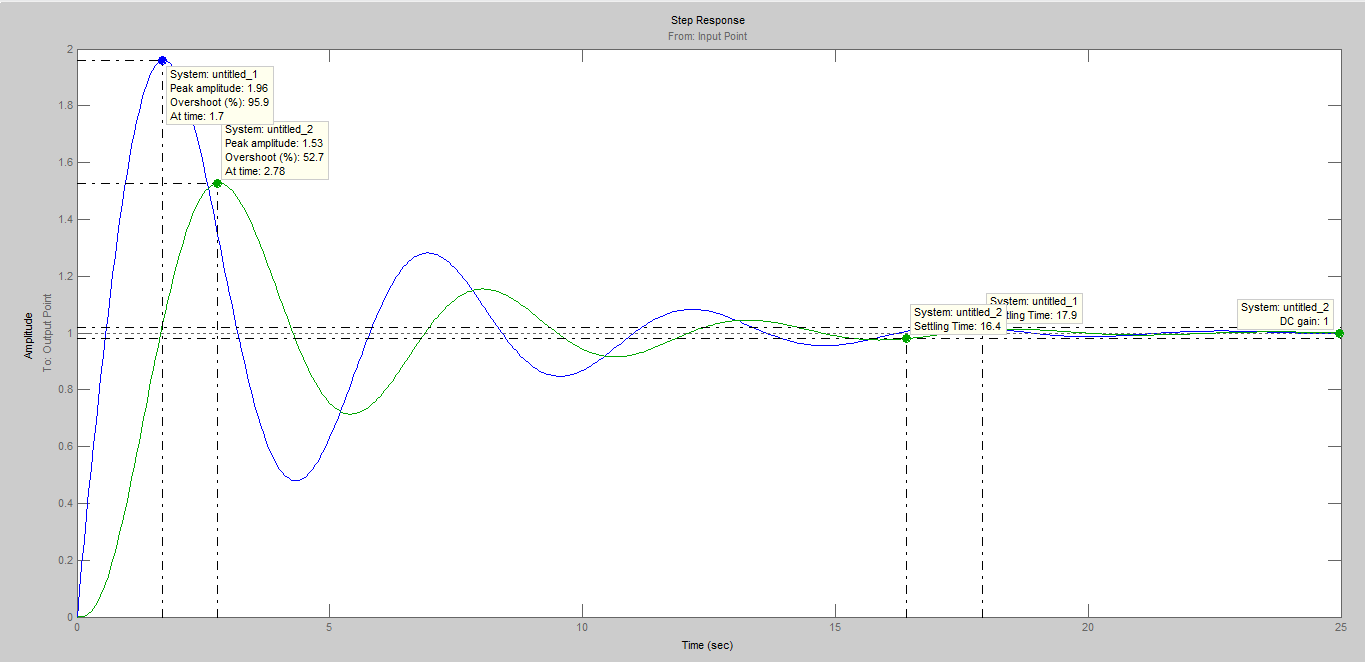
График переходного процесса для систем с учётом и не учётом действия внешнего возмущения