Понятие факторного анализа; детерминированное моделирование факторных систем.

Экономический анализ предполагает выявление некоторой совокупности факторов и установление формы и количественной характеристики их связи с исследуемым показателем. Каждое явление можно рассматривать и как причину, и как результат (например, производительность труда).

Экономический показатель, являющийся объектом исследования, называется результативным(обобщающим). Показатели, участвующие в исследовании как характеристики результативного и определяющие его величину, называются факторными.

Под факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативного показателя. В факторной системе может быть только один результативный показатель и один или более факторных. Выделение факторов как элементов факторной системы базируется на следующих критериях:

- причинности, т.е. любой фактор должен отражать причину изменения результативного показателя;

- самостоятельности;

- учетной возможности;

- количественной измеряемости.

В факторном анализе различают детерминированный и стохастический анализ.

Детерминированный анализпредставляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер. Это значит, что изучаемое явление можно разложить по прямым факторам, построив модель связи в виде произведения, частного или суммы факторов.

В детерминированном анализе выделяют следующие виды факторных моделей.

1 Аддитивные модели.Представлены формулой

n

у= Σ x_i = x₁+x₂+_...+x_n

i=1

Например, модель затрат на производство продукции y (З):

y(З)=х 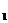(МЗ)+х 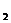(ЗП)+х 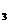(АО)+х 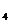(Проч.),

где МЗ – материальные затраты:

ЗП – заработная плата;

АО – амортизационные отчисления;

Проч. – прочие затраты.

2 Мультипликативные модели.Представлены формулой

n

у= Π x_i = x_{1 ×} x_{2 ×} x_{3 ×…×} x_n

i=1

Например, модель объема продукции y (О) можно представить в виде формулы

y (О) = x 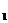(Ч) × x 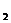(В),

где Ч – численность рабочих;

В – среднегодовая выработка одного рабочего.

3 Кратные модели.Представлены формулой

у = x₁/x_2.

Например, модель выработки продукции y(В) можно представить в виде формулы

y(В) = x 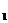(О) : x 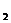(Ч).

4 Cмешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей. Они могут быть представлены в виде формул

у = (a +b)×c,

у = (a +b)/c

Например, коэффициент критической ликвидности

К_кр.л. = (ДС +КФВ +ДЗ) / КО ,

где ДС – денежные средства;

КФВ – краткосрочные финансовые вложения;

ДЗ – дебиторская задолженность;

КО – краткосрочные обязательства.

4.2 Приемы преобразования факторных систем.

Практика моделирования факторных систем позволяет преобразовывать их с целью включения в них новых факторных показателей. Для мультипликативных моделей это возможно путем разложения факторов исходной модели на факторы - сомножители.

Например, модель объема продукции У(О) можно представить формулой:

У(О)=х₁(В_год.)×х₂(Ч).

Здесь среднегодовую выработку рабочего (Вгод) можно представить в виде произведения факторов:

В_год. =В_час.×П×Д,

где В_час.– среднечасовая выработка рабочего,

П – продолжительность рабочего дня ,

Д – количество дней, отработанных рабочим за год.

Получим следующую формулу объёма продукции:

у(О)=х₁(В_час.)×х₂(П)×х₃(Д)×х₄(Ч).

Аналогично осуществляется моделирование аддитивных моделей за счет разложения факторных показателей на составные элементы.

Для кратных моделей применяются следующие способы их преобразования:

- удлинения;

- расширения;

- сокращения.

1 Прием удлинения предусматривает замену одного или нескольких факторов числителя на сумму однородных показателей. Если в исходной модели у = 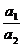фактор а₁ разложить на составляющие а₁₁, а₁₂,…а_1n, то она может быть преобразована следующим образом:

у = = + +…+ .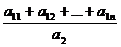

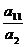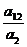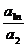Например, преобразуем показатель затрат на рубль товарной продукции (Z). Исходная модель:

Z= ,

где С – себестоимость продукции;

ТП – объём товарной продукции.

Представим себестоимость в виде суммы материальных затрат (МЗ), заработной платы (ЗП), амортизационных отчислений (АО) и прочих затрат (Проч.). Получим следующую факторную модель:

Z = = + + + .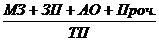

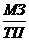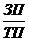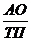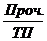В результате преобразования получена факторная модель, характеризующая зависимость затрат на 1 руб. товарной продукции от факторов эффективности использования различных ресурсов.

2 Прием расширения факторных моделей предусматривает расширение исходной модели за счет умножения и числителя и знаменателя дроби на одно и то же число.

y = 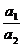(×b);

y = = × .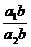

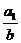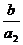Умножение можно производить на несколько чисел:

y = 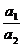(×bcd);

y= = × × ×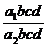

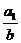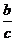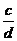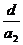
Например, преобразуем факторную модель среднегодовой выработки одного работника промышленно-производственного персонала (В ):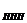

В = .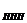

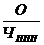Умножив и числитель, и знаменатель на показатель численности рабочих (Чр) получаем следующую формулу:

В 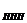= = 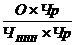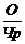× 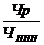= Вр×Ур

где Вр- среднегодовая выработка одного рабочего;

Ур- удельный вес рабочих в численности работников;

Чппп - численность работников промышленно-произодствен-ного персонала.

Таким образом, получена двухфакторная модель выработки одного работника, отражающая ее зависимость от выработки одного рабочего и структуры численности работающих.

3 Прием сокращения факторных моделей используется для создания новой факторной модели путем деления и числителя и знаменателя дроби на одно и то же число:

у= 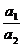( / b)

получаем

у=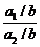

Например, преобразуем модель фондоотдачи (ФО):

ФО= ,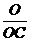

где О - объём продукции;

ОС - среднегодовая стоимость основных средств.

Разделим и числитель и знаменатель этой дроби на показатель среднесписочной численности рабочих (Чр):

ФО = 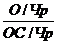= Вр :ФВ,

где ФВ – фондовооруженность рабочих.

Получим модель фондоотдачи, представленной отношением среднегодовой выработки рабочего (Вр) к фондовооружённости рабочих (ФВ).

На практике для преобразования одной и той же факторной модели могут быть последовательно использованы несколько методов.

Лекция 2

4.3 Прием цепных подстановок: сущность и правила применения

4.4 Прием абсолютных разниц: сущность и правила применения

4.5 Прием относительных разниц