Сущность и виды инвестиционного риска

Финансовые риски – это коммерческие риски. Риски бывают чистые и спекулятивные. Чистые риски означают возможность получения убытка или нулевого результата. Финансовые риски – это спекулятивные риски. Инвестор, осуществляя венчурное вложение капитала, заранее знает, что для него возможны только два вида результатов: доход или убыток. Особенностью финансового риска является вероятность наступления ущерба в результате проведения каких – либо операций в финансово – кредитной и биржевой сферах, совершения операций с фондовыми ценными бумагами, т.е. риска, который вытекает из природы этих операций. К финансовым рискам относятся кредитный риск, процентный риск, валютный риск, риск упущенной финансовой выгоды.

Спекулятивные

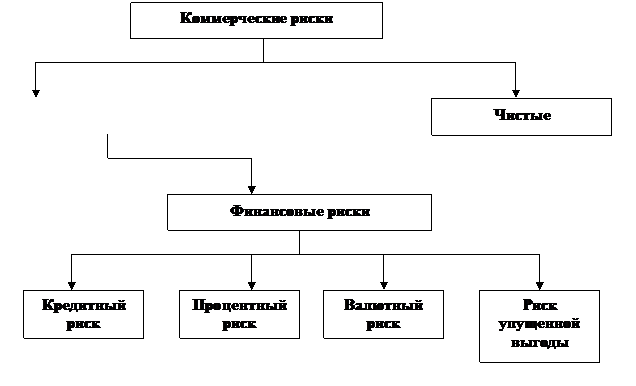
Кредитные риски – опасность неуплаты заемщиком основного долга и процентов, причитающихся кредитору. Процентный риск – опасность потерь коммерческими банками, кредитными учреждениями, инвестиционными фондами, селенговыми компаниями в результате превышения процентных ставок, выплачиваемых ими по привлеченным средствам, над ставками по предоставленным кредитам.

Валютные риски представляют собой опасность валютных потерь, связанных с изменением курса одной иностранной валюты по отношению к другой, в том числе национальной валюте при проведении внешнеэкономических, кредитных и других валютных операций.

Риск упущенной финансовой выгоды – это риск наступления косвенного финансового ущерба в результате неосуществления какого – либо мероприятия или остановки хозяйственной деятельности.

Величина риска или степень риска измеряется двумя критериями:

1) средне ожидаемое значение;

2) изменчивость возможного результата.

Среднее ожидаемое значение – это то значение величины события, которое связано с неопределенной ситуацией.

Изменчивость возможного результата представляет собой отклонения ожидаемого значения от средней величины. Для этого на практике обычно применяют два близко связанных критерия: дисперсию и среднее квадратическое отклонение. Дисперсия – среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых

G² = å(X -`X)²n / å n ,

где G2 – дисперсия

X – ожидаемое значение для каждого случая наблюдения;

`X – среднее ожидаемое значение;

n–число случаев наблюдение (частота)

Среднее квадратическое отклонение определяется по формуле:

G = Öå(X -`X)²n / å n,

Где G – среднее квадратическое отклонение.

При равенстве частот имеем частный случай

G² = å(X -`X)²n / å n ,

G = Öå(X -`X)²n / å n,

Среднее квадратическое отклонение является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия, и среднее квадратическое отклонение служат мерами абсолютной колеблемости. Для анализа обычно используют коэффициент вариации. Коэффициент вариации представляет собой отношение среднего квадратического отклонения к средней арифметической и показывает степень отклонения полученных значений

V = (±G / X ) * 100 (%),

где V – коэффициент вариации, %

Коэффициент вариации – относительная величина. Поэтому на его размер не оказывают влияния абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнить даже колеблемость признаков, выраженных в разных единицах измерения. Чем больше коэффициент, тем сильнее колеблемость.