Методы учета инфляции в финансовых расчетах
Владельцы денег не могут мириться с их обесцениванием в результате инфляции и предпринимают различные попытки компенсации потерь от снижения их покупательной способности.
Наиболее распространенным методом является индексация ставки процентов, по которой производится наращение, поскольку:
- если уровень инфляции равен ставке начисляемых процентов (τ = i), то реального роста денежных сумм не будет, т.к. наращение будет полностью поглощаться инфляцией;
- если уровень инфляции выше уровня процентной ставки (τ > i),то происходит "проедание" капитала, и реальная наращенная сумма будет меньше первоначальной денежной суммы;
- если уровень инфляции ниже процентной ставки (τ < i), то это будет соответствовать росту реальной денежной суммы.
В связи с этим вводится понятие номинальная ставка процента, т.е. ставки с поправкой на инфляцию (iτ).
Общая формула для определения простой ставки процентов, компенсирующей ожидаемую инфляцию, имеет следующий вид:
iτ = [(1 + n i) • Jτ - 1] : n
где i – простая ставка процентов, характеризующая требуемую реальную доходность финансовой операции (нетто-ставка);
iτ – процентная ставка с поправкой на инфляцию.
Пример. Банк выдал клиенту кредит на один год в размере 20 тыс. руб. по ставке 6% годовых. Уровень инфляции за год составил 18%. Определить с учетом инфляции реальную ставку процентов по кредиту, погашаемую сумму и сумму процентов за кредит.
Решение:
Номинальная наращенная сумма
FV = PV(1 + n i) = 20'000 (1 + 0,06) = 21'200,00 руб.
Номинальные начисленные проценты
I = FV - PV = 21'200 - 20'000 = 1'200,00 руб.
Реальная наращенная сумма
FVτ = FV / (1 + τ = 21'200 / 1,18 = 17'966,10 руб.
Реальные проценты
Iτ = FVτ - PV = 17'966,10 - 20'000 = -2'033,90 руб.
Таким образом, получен убыток от данной финансовой операции в размере 2'033,90 руб.
Ставка по кредиту с учетом инфляции должна быть равна
iτ = [(1 + n i) • Iτ - 1] : n = (1,06 • 1,18 - 1) / 1 = 0,2508
Наращенная сумма
FV = PV(1 + n i) = 20'000 (1 + 0,2508) = 25'016,00 руб.
Доход банка
I = FV - PV = 25'016 - 20'000 = 5'016,00 руб.
Реальный доход банка
Iτ = FVτ - PV = 25'016 / 1,18 - 20'000 = 1'200,00 руб.
Реальная доходность финансовой операции
i = Iτ / PV =1'200 / 20'000 = 0,06
Таким образом, чтобы обеспечить доходность в размере 6% годовых, ставка по кредиту с учетом инфляции должна соответствовать 25,1% годовым.
Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле
iτ = i + τ + iτ
Пример. Определить номинальную ставку процентов для финансовой операции, если уровень эффективности должен составлять 7% годовых, а годовой уровень инфляции 22%.
Решение:
Процентная ставка с учетом инфляции
iτ = i + τ + iτ = 0,07 + 0,22 + 0,07 • 0,22 = 0,3054
Таким образом, номинальная ставка составляет 30,54% при реальной ставке 7%.
Для расчета номинальной ставки можно использовать следующую модель:
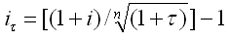 |
из которой можно сравнивать уровни процентной ставки и инфляции, проводить анализ эффективности вложений и устанавливать реальный прирост вложенного капитала.
При начислении процентов несколько раз в год
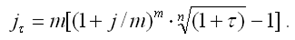 |
Эти модели позволяют производить учет инфляции и корректировку процентных ставок.
На практике довольно часто довольствуются сравнением i и τ путем вычисления реальной ставки, т.е. уменьшенной ставки доходности на уровень инфляции:
i = (i - τ) / (1 + τ)
Пример. Определить реальную ставку при размещении средств на год под 35% годовых, если уровень инфляции за год составляет 30%.
Решение:
Определяем реальную ставку:
i = (0,35 - 0,2) / (1 + 0,2) = 0,125
Таким образом, реальная ставка 12,5% годовых.
