Финансово-экономические расчеты

Приложение

Финансово-экономические расчеты

Еще одна важная сфера приложения MS Excel связана с осуществлением финансовых расчетов. Финансовые вычисления включают в себя совокупность методов и расчетов, используемых при принятии управленческих решений, - от элементарных арифметических операций и до сложных алгоритмов построения многокритериальных моделей, позволяющих получить оптимальные характеристики коммерческих сделок в зависимости от различных условий их проведения. Проведение подобных вычислений — трудоемкая процедура, требующая определенной математической подготовки, а также использования большого количества справочных материалов.

На данный момент стандартный курс финансовых вычислений включает в себя следующие основные темы:

- логика финансовых операций (временная ценность денег, операции наращения и дисконтирования и т. д.);

- простые проценты (операции наращения и дисконтирования, налоги, инфляция, замена платежей);

- сложные проценты (то же и эквивалентность ставок, операции с валютой и т. п.);

- денежные потоки;

- анализ эффективности инвестиционных проектов;

- оценка финансовых активов.

В Excel реализовано 15 встроенных и 37 дополнительных финансовых функций.

По типу решаемых задач все финансовые функции Excel можно разделить на следующие условные группы:

- функции для расчета амортизационных платежей;

- функции для анализа аннуитетов и инвестиционных проектов;

- функции для анализа ценных бумаг;

- вспомогательные функции.

Функции каждой группы имеют практически одинаковый набор обязательных и дополнительных (необязательных) аргументов.

Рассмотрим несколько функций для расчета амортизационных отчислений.

Функция ДДОБ – функция, определяющая значение амортизации имущества за данный период, используя метод двойного процента со снижающегося остатка или иной явно указанный метод.

Общий вид: = ДДОБ(стоимость; остаточная_стоимость; время_эксплуатации; период; коэффициент)

Работает так: вычисляет амортизацию за заданный период по следующей формуле:

ДДОБ=((стоимость - остаточная_стоимость) - суммарная амортизация за предшествующие периоды) * (коэффициент / время_эксплуатации).

В этой формуле Стоимость — это начальная стоимость имущества;

Остаточная_стоимость — это стоимость в конце периода амортизации (иногда называется остаточной стоимостью имущества);

Время_эксплуатации — это количество периодов, за которые собственность амортизируется (иногда называется периодом амортизации);

Период — это период, для которого требуется вычислить амортизацию. Период должен быть измерен в тех же единицах, что и время_эксплуатации.

Коэффициент — это норма снижения балансовой стоимости (амортизации). Если аргумент опущен, то он полагается равным 2 (метод удвоенного процента со снижающегося остатка).

Все пять аргументов должны быть положительными числами.

Примеры

Предположим, что предприятие приобрело новую машину. Машина стоит 2 400 руб. и имеет срок службы 10 лет. Остаточная стоимость составляет 300 руб. Следующие примеры показывают амортизацию за несколько периодов. Результаты округляются до двух знаков после запятой.

Вычислим амортизацию машины за первый день эксплуатации. Формула =ДДОБ(2400;300;3650;1)) выдает ответ «1,32р.», т.е. амортизация за первый день составляет 1,32 р. Microsoft Excel автоматически предполагает, что коэффициент равен 2, в этой формуле срок эксплуатации исчисляется в днях, поскольку нам надо вычислить амортизацию за первый день.

Вычислим амортизацию машины за первый месяц эксплуатации. Формула =ДДОБ(2400;300;120;1) выдает ответ «40,00р.», т.е. амортизация за первый месяц составляет 40,00 р. Microsoft Excel автоматически предполагает, что коэффициент равен 2, в этой формуле срок эксплуатации исчисляется в месяцах, поскольку нам надо вычислить амортизацию за первый месяц.

Вычислим амортизацию машины за третий год эксплуатации при коэффициенте амортизации 1,5. Формула =ДДОБ(2400;300;10;3;1,5) выдает ответ «260,10р.», т.е. амортизация за третий год из 10 лет составляет 260,10 р. при коэффициенте амортизации 1,5. В этой формуле срок эксплуатации исчисляется в годах, поскольку нам надо вычислить амортизацию за третий год.

Примеры

По вкладу размером в 2000 руб. начисляется 10% годовых. Определим, какая сумма окажется на сберегательном счете через 5 лет, если проценты начисляются ежемесячно.

По следующей формуле вычисляем:

= БС(10%/12; 5*12; ; -2000) равняется 3290,62 руб.

Определим, какая сумма окажется на счете, если 2000 руб. положены на 4 года под 13,5 % годовых. Проценты начисляются каждые пол года.

По следующей формуле вычисляем:

= БС(13,5%/2; 4*2; ; -2000) равняется 3372,66 руб.

На сберегательный счет вносятся платежи по 3000 руб. в начале каждого месяца. Определим, какая сумма окажется на счете через 4 года при ставке 12% годовых.

По следующей формуле вычисляем:

= БС(12%/12; 4*12; -3000; 0; 1) равняется 185504,5 руб.

Функция ПС – функция, определяющая текущую стоимость единой суммы и будущих фиксированных периодических платежей,т.е. возвращает текущий объем вклада. Текущий объем — это общая сумма, которую составят будущие платежи. Например, когда деньги берутся взаймы, заимствованная сумма и есть текущий объем для заимодавца.

Общий вид: = ПС(ставка;кпер;выплата;бз;тип)

Работает так: вычисляет сумму, которую необходимо положить на счет сегодня, чтобы она в конце число_периодов она достигла заданного значения бз за заданный период, по следующей формуле

,

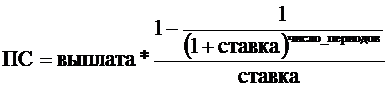если в течении указанного периода проводились отчисления или начисления и эти операции проводились в конце каждого периода, и по формуле

,

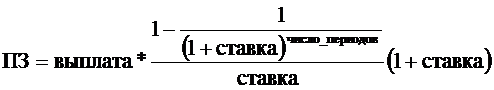если операции начисления или отчисления проводились в начале периода.

Если требуется определить текущее значение вклада, т.е. сумму, сумму, которую необходимо положить на счет сегодня, чтобы она в конце число_периодов она достигла заданного значения бз, то значение функции ПЗ определяется по формуле:

.

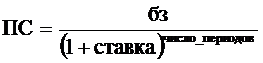В этих формулах ставка - это учетная ставка за один период;

кпер— это общее число периодов выплат годовой ренты;

выплата— это выплата, производимая в каждый период и не меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи и платежи по процентам, но не включают других сборов или налогов.

бз — требуемое значение будущей стоимости или остатка средств после последней выплаты. Если аргумент опущен, он полагается равным 0 (будущая стоимость займа, например, равна 0).

тип — число 0 или 1, обозначающее, что выплата должна производиться в конце периода или в начале периода соответственно.

Примеры

Предположим, что выкупается страховка, по которой выплачивается по 500 руб. в конце каждого месяца в течение 20 последующих лет. Стоимость ренты составляет 60 000 руб. и выплачиваемые деньги принесут 8 процентов годовых. Необходимо определить, будет ли это хорошим способом инвестировать капитал.

По следующей формуле вычисляем:

=ПС(0,08/12; 12*20; 500; ; 0) равняется -59 777,15 руб.

Результат получается отрицательный, поскольку он представляет деньги, которые необходимо выплатить. Настоящий объем вклада (59 777,15 руб.) меньше, чем запрашиваемая цена (60 000 руб.). Следовательно, можно сделать вывод, что это не самый лучший способ инвестирования денег.

Рассчитаем текущую стоимость вклада, который через 3 года составит 15000 руб. при начислении 20% в год. Используя функцию ПЗ получаем, что настоящий объем вклада составит:

=ПС(0,2; 3; 0; 15000; 0) равняется -8680,56 руб.

Определим текущую стоимость обычных ежеквартальных платежей размером в 350 руб. в течение 7 лет, если ставка – 11% годовых.

По следующей формуле вычисляем:

=ПС(0,11/4; 7*4; -350; ; 0) равняется -6772,79 руб.

Примечания

Если дата_согл или дата_вступл_в_силу не является допустимой датой, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Если ставка < 0, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Если цена ≤ 0 или погашение ≤ 0, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Если частота — любое число, отличное от 1, 2 или 4, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Если базис < 0 или базис > 4, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Если дата_согл ≥ дата_вступл_в_силу, функция ДОХОД возвращает значение ошибки #ЧИСЛО!.

Примеры

Облигации приобретены 6.9.1993 по курсу 89 руб. и имеют купонный доход в размере 9%, который выплачивается с периодичностью – раз в полугодие. Предполагаемая дата погашения облигации – 12.9.1997 по курсу 100 руб. Необходимо определить годовую ставку помещения облигации.

По следующей формуле вычисляем:

=ДОХОД(ДАТА(1993; 09;06); ДАТА(1997;09;12); 0,09; 89; 100; 2) равняется 12,57%.

Облигации приобретены 17.7.1996 по цене 50 руб. и имеют купонный доход в размере 10%, который выплачивается с периодичностью – раз в квартал. Предполагаемая дата погашения облигации – 1.01.1998 по курсу 100 руб. Необходимо определить годовую ставку помещения облигации по фактическому числу дней в месяце.

По следующей формуле вычисляем:

=ДОХОД(ДАТА(1996;7;17); ДАТА(1998;1;1); 10%; 50; 100; 4; 1) равняется 65,96%.

Функция ЦЕНА – функция, вычисляющая курс (цену) покупки ценной бумаги с периодическими выплатами купонных процентов, т.е. возвращает цену за 100 рублей номинальной стоимости ценных бумаг, по которым выплачивается периодический процент.

Общий вид: = ЦЕНА(дата_согл; дата_вступл_в_силу; ставка; доход; погашение; частота; базис)

Работает так: вычисляет доходность облигаций по очень сложной формуле, которая приводится в справке Microsoft Excel и параметрами которой являются:

Дата_согл — дата расчета за ценные бумаги (более поздняя, чем дата выпуска, когда ценные бумаги были проданы покупателю);

Дата_вступл_в_силу — срок погашения ценных бумаг. Эта дата определяет момент истечения срока действия ценных бумаг.

Ставка — годовая процентная ставка для купонов по ценным бумагам;

Доход — годовой доход по ценным бумагам;

Погашение — выкупная стоимость ценных бумаг за 100 руб. номинальной стоимости;

Частота — количество выплат по купонам за год. Для ежегодных выплат частота = 1; для полугодовых выплат частота = 2; для ежеквартальных выплат частота = 4.

Базис — используемый способ вычисления дня (таблица Б.1).

Примечания

Дата соглашения является датой продажи покупателю купона, например облигации. Срок платежа представляет собой дату истечения срока действия купона.

Если дата_согл или дата_вступл_в_силу не является допустимой датой, то функция ЦЕНА возвращает значение ошибки #ЗНАЧ!.

Если доход < 0 или ставка < 0, то функция ЦЕНА возвращает значение ошибки #ЧИСЛО!.

Если погашение ≤ 0, то функция ЦЕНА возвращает значение ошибки #ЧИСЛО!.

Если частота любое число отличное от 1, 2 или 4, то функция то функция ЦЕНА возвращает значение ошибки #ЧИСЛО!.

Если базис < 0 или если базис > 4, то функция ЦЕНА возвращает значение ошибки #ЧИСЛО!.

Если дата_согл ≥ дата_вступл_в_силу, то функция ЦЕНА возвращает значение ошибки #ЧИСЛО!.

Примеры

Облигации приобретены 6.9.1993 и погашены 12.9.1997. Размер купонной ставки – 9% с выплатой раз в полугодие. Ожидаемая годовая ставка помещения (доход) – 12,57%, номинал облигации (погашение) – 100 руб., базис расчета – 1. Необходимо определить курс покупки облигации.

По следующей формуле вычисляем:

=ЦЕНА(ДАТА(1993;09;06); ДАТА(1997;09;12); 0,09; 0,1257; 100; 2; 1) равняется 89 руб.

Облигация приносит 45% годового дохода, срок действия облигации с 20.9.1996 по 20.9.1998. Купон в размере 30% годовых выплачивается раз в полугодие. Необходимо определить курс покупки облигации 1.12.1996.

По следующей формуле вычисляем:

=ЦЕНА(ДАТА(1996;12;1); ДАТА(1998;9;20); 30%; 45%; 100; 2; 1) равняется 82,35 руб.

Функция НАКОП ДОХОД – функция, вычисляющая накопленный на момент приобретения ценной бумаги купонный доход (сумму), т.е. возвращает накопленный процент по ценным бумагам с периодической выплатой процентов.

Общий вид: =НАКОПДОХОД(дата_выпуска; первый_доход; дата_согл; ставка; номинал; частота; базис)

Работает так: вычисляет купонный доход облигаций по слудующей формуле:

,

где, A_j - число накопленных дней для i-го квазикупонного периода в оставшемся периоде выплат.

NC - число квазикупонных периодов, которые укладываются в оставшийся период. Если это число содержит дробную часть, то оно округляется с избытком до следующего целого.

NL_j - нормальная продолжительность в днях i-ого квазикупонного периода в оставшемся периоде;

Дата_выпуска - дата выпуска ценных бумаг;

Первый_доход - это дата первой выплаты по ценным бумагам.

Дата_согл - дата расчета за ценные бумаги (более поздняя, чем дата выпуска, когда ценные бумаги были проданы покупателю);

Ставка - годовая процентная ставка для купонов по ценным бумагам;

Номинал — это номинальная стоимость ценных бумаг. Если номинал опущен, то функция НАКОПДОХОД использует значение 1000 руб.

Частота — количество выплат по купонам за год. Для ежегодных выплат частота = 1; для полугодовых выплат частота = 2; для ежеквартальных выплат частота = 4.

Базис — используемый способ вычисления дня (таблица Б.1).

Примечания

Если дата_выпуска, первый_доход или дата_согл не являются допустимой датой, то функция НАКОПДОХОД возвращает значение ошибки #ЗНАЧ!.

Если ставка ≤ 0 или номинал ≤ 0, то функция НАКОПДОХОД возвращает значение ошибки #ЧИСЛО!.

Если частота является любым числом, отличным от 1, 2 или 4, то функция НАКОПДОХОД возвращает значение ошибки #ЧИСЛО!.

Если базис < 0 или базис > 4, то функция НАКОПДОХОД возвращает значение ошибки #ЧИСЛО!.

Если дата_выпуска ≥ дата_согл, НАКОПДОХОД возвращает значение ошибки #ЧИСЛО!.

Примеры

Облигация номиналом 5000 руб., выпущенная 1.7.1996, приобретена 12.9.1996. Периодичность купонных выплат в размере 40% годовых – ежеквартальная. Дата первой купонной выплаты – 1.10.1996. Определите накопленный на момент приобретения доход.

По следующей формуле вычисляем:

=НАКОПДОХОД(ДАТА(1996;7;1); ДАТА(1996;10;1); ДАТА(1996;9; 12); 40%; 5000; 4; 1) равняется 396,47 руб.

Облигация номиналом 100000 руб. выпущена 1.1.1996 и имеет купон 15% годовых с выплатой 1 раз в квартал. Определите размер первой купонной выплаты, которая будет через квартал.

По следующей формуле вычисляем:

=НАКОПДОХОД(ДАТА(1996;1;1); ДАТА(1996;4;30); ДАТА(1996;4; 30); 0,15; 100000; 4; 1) равняется 4972,82 руб.

Таблица соответствия наименований функций в разных версиях Microsoft Excel

Microsoft Excel 2000	Microsoft Excel 2007 (XP)
АМГД	АМЧ
АМР	АПЛ
БЗ	БС
НПЗ	ЧПС
ОСНПЛАТ	ОСПЛТ
ПЗ	ПС
ППЛАТ	ПЛТ
ПЛПРОЦ	ПРПЛТ
ВНДОХ	ВСД

Приложение

Финансово-экономические расчеты

Еще одна важная сфера приложения MS Excel связана с осуществлением финансовых расчетов. Финансовые вычисления включают в себя совокупность методов и расчетов, используемых при принятии управленческих решений, - от элементарных арифметических операций и до сложных алгоритмов построения многокритериальных моделей, позволяющих получить оптимальные характеристики коммерческих сделок в зависимости от различных условий их проведения. Проведение подобных вычислений — трудоемкая процедура, требующая определенной математической подготовки, а также использования большого количества справочных материалов.

На данный момент стандартный курс финансовых вычислений включает в себя следующие основные темы:

- логика финансовых операций (временная ценность денег, операции наращения и дисконтирования и т. д.);

- простые проценты (операции наращения и дисконтирования, налоги, инфляция, замена платежей);

- сложные проценты (то же и эквивалентность ставок, операции с валютой и т. п.);

- денежные потоки;

- анализ эффективности инвестиционных проектов;

- оценка финансовых активов.

В Excel реализовано 15 встроенных и 37 дополнительных финансовых функций.

По типу решаемых задач все финансовые функции Excel можно разделить на следующие условные группы:

- функции для расчета амортизационных платежей;

- функции для анализа аннуитетов и инвестиционных проектов;

- функции для анализа ценных бумаг;

- вспомогательные функции.

Функции каждой группы имеют практически одинаковый набор обязательных и дополнительных (необязательных) аргументов.

Рассмотрим несколько функций для расчета амортизационных отчислений.