Определение срока постоянной ренты постнумерандо
В таблице 2 приведены формулы для расчета срока постоянных рент постнумерандо. Они выводятся из формул (3.1) – (3.21).
Пример 7. Какой необходим срок для накопления 100000 руб. при условии, что в конце каждого месяца вносится 1000 руб., а на взносы начисляются проценты по сложной ставке 25% годовых?
| Имеем: S = 100000 руб. Rp = 1000 руб. р = 12 ic = 0,25 | Решение: Так как рента срочная, постнумерандо, проценты начисляются один раз в год, то срок ренты находится по формуле (4.5). |
| n = ? | Годовая сумма платежей: R = Rp × p = 1000 × 12 = 12000 руб. Срок: 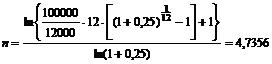 года. года. |
Так как взносы ежемесячные, переведем дробную часть решения в месяцы.
0,7356 года = 0,7356 × 12 мес. = 8,8272 мес. < 9 мес.
Полученный результат говорит о том, что после внесения очередного взноса через 4 года и 9 месяцев накопленная сумма впервые превысит нужную сумму в размере 100000 руб.
Следует отметить, что мы неявно предполагаем, что при закрытии счета в указанный момент банк за каждый месяц неполного пятого года начислит проценты по сложной ставке 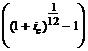 за месяц.
за месяц.
В нашем примере это составит 1,88% в месяц.
Проверим правильность решения. При ставке 1,88% в месяц за 57 месяцев (4 года 9 месяцев) и ежемесячной выплате 1000 руб. наращенная сумма составит:
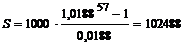 руб.
руб.
Задача для самостоятельного решения
7. Определите срок, за который сумма фонда составит 100 тыс. руб., если в фонд вносится по 10 тыс. руб. в конце каждого года и на них ежеквартально начисляются проценты по сложной ставке 8% годовых.
Таблица 2
Формулы для расчета срока постоянных рент постнумерандо
| Количество платежей в году | Количество начислений процентов в году | Сроки платежей | |
| S | A | ||
| p = 1 | m = 1 | 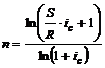 (4.1) (4.1) | 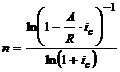 (4.2) (4.2) |
| годовая рента | m > 1 | 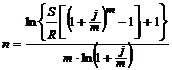 (4.3) (4.3) | 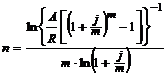 (4.4) (4.4) |
| р > 1 | m = 1 | 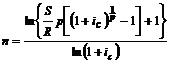 (4.5) (4.5) | 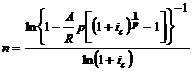 (4.6) (4.6) |
| срочная рента | m =p | 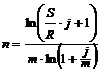 (4.7) (4.7) | 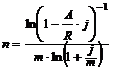 (4.8) (4.8) |
| m ¹ p | 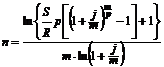 (4.9) (4.9) | 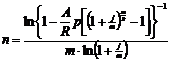 (4.10) (4.10) |
4.3. Определение процентной ставки финансовой ренты
приближенным методом
В отличие от размера платежа и срока ренты процентная ставка не может быть выражена в явной форме. Поэтому для ее нахождения используются приближенные методы.
Чаще всего используют метод линейной интерполяции.
Для нахождения приближенного значения годовой сложной ставки iс,если известны срок ренты и коэффициент наращения 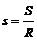 , применяется следующая интерполяционная формула:
, применяется следующая интерполяционная формула:
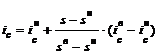 , (4.11)
, (4.11)
где 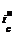 и
и 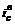 — верхнее и нижнее значения процентной ставки, между которыми находится искомое значение ic.
— верхнее и нижнее значения процентной ставки, между которыми находится искомое значение ic.
Эти два значения находятся путем подбора так, чтобы было sн < s < sв.
Здесь s — коэффициент наращения, для которого определяется размер ставки ic; 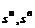 — коэффициенты наращения для верхнего и нижнего значений процентной ставки
— коэффициенты наращения для верхнего и нижнего значений процентной ставки 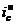 и
и 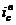 .
.
Если известен коэффициент приведения ренты 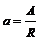 , то применяется формула
, то применяется формула
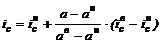 , (4.12)
, (4.12)
где а — коэффициент приведения, для которого определяется размер ставки ic;
ан, ав — коэффициенты приведения для верхнего и нижнего значений процентной ставки 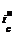 и
и 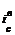 .
.
Вычисления по формулам (4.11) и (4.12) могут быть проделаны многократно до получения требуемой точности.
Пример 8. Планируется вносить в банк в течение семи лет в конце каждого года по 10000 руб. Какова должна быть годовая ставка сложных процентов, чтобы к концу срока было накоплено 100000 руб.?
| Имеем: S = 100000 руб. R = 10000 руб. n = 7 | Решение: 1. Находим коэффициент наращения s: 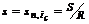 = 100000 : 10000 = 10. = 100000 : 10000 = 10. |
| ic - ? | 2. Выберем значения 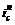 = 11%, = 11%, 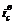 = 12%. Для этих значений ставок находим коэффициенты наращения sн и sв. = 12%. Для этих значений ставок находим коэффициенты наращения sн и sв. |
Так как рента годовая, постнумерандо, проценты начисляются один раз в год, то коэффициент наращения определяется по формуле:
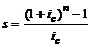 . (4.13)
. (4.13)
Для нижнего значения предполагаемой ставки коэффициент наращения равен по формуле (4.13):
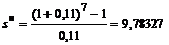 .
.
Для верхнего значения предполагаемой ставки коэффициент наращения равен по формуле (4.13):
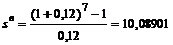 .
.
Отсюда ic определяем по формуле (4.11):
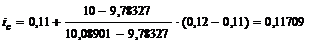 или 11,709%.
или 11,709%.
КОНВЕРСИЯ ФИНАНСОВЫХ РЕНТ
В практической деятельности возникают случаи, когда на этапе разработки контракта или в ходе его выполнения необходимо изменить поток платежей. Например, несколько платежей ренты заменить одним, или заменить ренту с одними параметрами на ренту с другими параметрами. Такие операции называются конвертированием условий финансовой ренты. Конверсия не приводит к изменению финансовых последствий для каждой из участвующих сторон, если она основывается на принципе финансовой эквивалентности обязательств.
Простые конверсии
К простым конверсиям относят выкуп ренты изамену разового платежа рентой.
При выкупе ренты размер выкупа предполагается равным современной стоимости выкупаемой ренты.
При замене разового платежа рентой параметры ренты подбираются так, чтобы ее современная стоимость совпала с размером платежа.
Пример 9. Фирма предлагает покупателю свою продукцию на сумму 50 тыс. руб. с условием ее оплаты в рассрочку в течение одного года под сложные проценты, которые будут начисляться два раза в год по ставке 20% годовых. Платежи должны вноситься ежеквартально.
Определить размер платежа.
| Имеем: А = 50000 руб. n = 1 p = 4 j = 0,2 m = 2 | Решение: Платежи покупателя за продукцию будут представлять собой финансовую срочную ренту постнумерандо с начислением процентов два раз в год. Для определения размера платежа воспользуемся формулой (4.10) |
| Rp = ? | 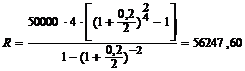 руб. Rp = R : p = 56247,60 : 4 = 14061,9 руб. руб. Rp = R : p = 56247,60 : 4 = 14061,9 руб. |
Изменение условий ренты
Изменение условий ренты по существу означает замену одной ренты другой. Если замена базируется на принципе финансовой эквивалентности, то из этого следует равенство современных величин обеих рент.
В качестве примера приведем случай, когда внесение первого взноса ренты переносится на более поздний срок (t лет, месяцев). При этом общая продолжительность ренты, размеры платежей могут оставаться прежними или измениться.
Пусть первоначально имеется постоянная рента постнумерандо имеет параметры R1 и n1. Необходимо конвертировать ренту, отсрочив выплаты на t лет и заменив параметры на R2 и n2.
В соответствии с принципом финансовой эквивалентности должны быть равны современные величины первоначальной и отсроченной рент.
А1 = А2.
Вычислим их на момент начала первоначальной ренты.
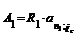
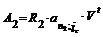 ,
,
где 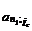 ,
, 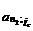 — коэффициенты приведения первоначальной годовой
— коэффициенты приведения первоначальной годовой
ренты;
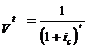 — дисконтный множитель за период t, на который
— дисконтный множитель за период t, на который
отложена рента.
Рассмотрим один из примеров замены параметров ренты.
Пример 10. Банк предлагает к продаже объект залогового имущества стоимостью 400 тыс. руб. Банк выставил условия продажи: стоимость объекта погашается ежегодными равными платежами, вносимыми в конце года, срок погашения 4 года, сложная процентная ставка 4% годовых, проценты начисляются два раза в год. Покупатель предлагает свои условия: платежи производить 2 раза в год и проценты на них начислять два раза в год, по ставке 6% годовых, со сроком выплаты 6 лет. Определить величину рентного платежа, предложенного продавцом и покупателем.
| Имеем: А1 = А2 = 400 тыс. руб. n1 = 4 n2 = 6 J1 = 0,04 j2 = 0,06 m1 = m2 = 2 p1 = 1 p2 = 2 | Решение: По условию имеются две эквивалентные ренты с известной общей современной стоимостью. Известны все параметры рассматриваемых рент, за исключением размеров платежей. Найдем их с помощью формул таблицы 1. |
| R1 - ? R2 - ? |
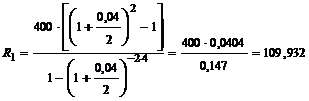 тыс. руб.
тыс. руб.
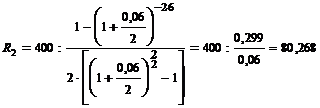 тыс. руб.
тыс. руб.
Задача для самостоятельного решения
8. Фирма по торговле недвижимостью продает квартиру за 120 тыс. руб. на условиях оплаты в течение двух лет равными платежами, вносимыми в конце года с учетом 6% сложных годовых.
Покупатель предлагает оплату с отсрочкой платежей один год с сохранением цены и процентной ставки.
Определите размеры платежей для обоих вариантов.
Консолидация рент
Консолидация (объединение) рент — это замена нескольких рент одной, основанная на принципе финансовой эквивалентности.
При консолидации рент современная величина новой консолидированной ренты равна сумме современных величин заменяемых рент.
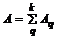 , (5.1)
, (5.1)
где А — современная величина консолидированной ренты;
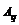 — cовременная величина q-й заменяемой ренты, q = 1, 2, ..., к.
— cовременная величина q-й заменяемой ренты, q = 1, 2, ..., к.
Основные параметры, которые характеризуют консолидированную ренту, — это размер платежей ренты и ее продолжительность.
Размер платежей консолидированной ренты
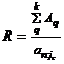 , (5.2)
, (5.2)
где 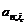 — коэффициент приведения консолидированной ренты.
— коэффициент приведения консолидированной ренты.
При консолидации годовых рент с начислением процентов в конце
каждого года, различающихся между собой размером платежей, продолжительностью ренты, процентными ставками, размер платежей консолидированной ренты можно определить по формуле:
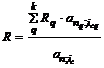 , (5.3)
, (5.3)
где Rq — размер платежей;
nq — продолжительность;
icq — процентная ставка q-й ренты.
Пример 11. Имеются две годовые ренты постнумерандо с начислением процентов в конце периода. Их необходимо заменить одной годовой рентой с начислением процентов по ставке 7% сложных годовых и сроком 4 года. Начало срока консолидированной ренты совпадает с началом срока платежей данных рент.
Параметры заменяемых рент даны в таблице 3.
Таблица 3
| Номер ренты q | Размер платежей ренты Rq, тыс. руб | Срок ренты nq, лет | Годовая процентная ставка icq, % | Коэффициент приведения 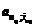 | Современная величина 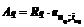 , тыс. руб. , тыс. руб. |
| 2,5 | 8,0 | 3,312127 | 8,28032 | ||
| 3,7 | 7,0 | 4,100197 | 15,17073 | ||
| Итого | 23,45105 |
Определяем величину рентного платежа консолидированной ренты по формуле (5.2).
Коэффициент приведения консолидированной ренты 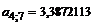 .
.
Размер платежа консолидированной ренты:
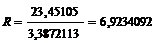 тыс. руб.
тыс. руб.
ОТВЕТЫ К ЗАДАЧАМ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. 90169,75 руб.
2. 1306,59 руб.
3. 283785,37 руб.
4. 953420 руб.
5. 266,26 руб.
6. 33444,82 руб.
7. 7 лет 9 месяцев.
8. 65454,54 руб. 69381,81 руб.
ПРИЛОЖЕНИЕ 1
ТЕСТОВЫЕ ЗАДАНИЯ
1. Поток платежей, все члены которого положительные величины,
а временные интервалы между платежами одинаковы, называют ...
а) финансовой рентой
б) очередностью
в) аннуитетом
2. Основными параметрами, характеризующими ренту, являются ...
а) размер платежа
б) момент платежа
в) срок ренты
г) период ренты
д) процентная ставка
3. По количеству выплат членов ренты на протяжении года ренты делятся на ...
а) годовые
б) бессрочные
в) р-срочные
4. По моменту платежа в пределах периода ренты бывают ...
а) постнумерандо
б) пренумерандо
5. По величине размеров платежей ренты делятся на ...
а) непрерывные
б) постоянные
в) переменные
6. Обобщающими характеристиками ренты являются ...
а) размер платежа ренты
б) наращенная сумма
в) современная величина
7. По какой формуле определяется наращенная сумма годовой финансовой ренты постнумерандо с начислением процентов на платежи несколько раз в году?
а) 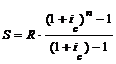
б) 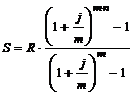
в) 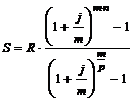
8. По Приложению 2 определите, чему равен коэффициент наращения годовой ренты постнумерандо сроком 10 лет с начислением процентов по сложной годовой ставке 7% ...
а) 13,18079494
б) 13,81644796
в) 13,924574
9. По Приложению 2 определите, чему равен коэффициент приведения годовой ренты постнумерандо сроком 11 лет с начислением процентов по годовой сложной ставке 8 % ...
а) 7,354233898
б) 7,498674337
в) 7,138964258
10. Чему равен размер очередного платежа р-срочной ренты, если годовая сумма платежей составляет 5808 руб., а платежи вносятся ежеквартально.
а) 1452 руб.
б) 23232 руб.
в) 1454 руб.
11. По какой формуле определяется наращенная сумма р-срочной ренты пренумерандо, если проценты начисляются несколько раз в году?
а) 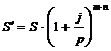
б) 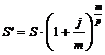
в) 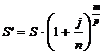
12. По какой формуле определяется современная величина годовой ренты постнумерандо с начислением процентов несколько раз в году?
а) 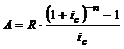
б) 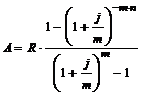
в) 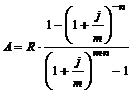
13. По каким формулам определяется размер очередного платежа р-срочной ренты постнумерандо, когда количество платежей совпадает с количеством раз начисления процентов в году?
а) 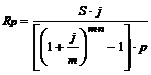
б) 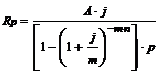
в) 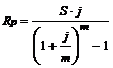
г) 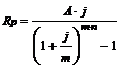
14. Консолидация рент — это ...
а) сохранение параметров ренты
б) объединение нескольких рент в одну, основанное на принципе финансовой эквивалентности
15. Переменная рента — это ...
а) поток платежей, члены которого не являются постоянными величинами
б) поток платежей, на которые начисляются проценты по различным значениям процентных ставок
ОТВЕТЫ
| 1.а, в | 6. б, в | 11.б |
| 2. а, в, г, д | 7. б | 12. б |
| 3. а, в | 8. б | 13.а, б |
| 4. а, б | 9. в | 14.б |
| 5. б, в | 10.а | 15.а |
ПРИЛОЖЕНИЕ 2
