Определить накопленную сумму к концу срока ренты.
Схематично условие задачи показано на рисунке.
100 тыс. руб. 100 тыс. руб. 100 тыс. руб.
 |  |  |

 ·-------- S-?
·-------- S-?
01.01.1998 01.01.1999 01.01.2000 01.01.2001
Введем обозначения:
R — величина члена ренты ;
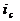 — cложная процентная ставка;
— cложная процентная ставка;
n — срок ренты в годах.
Все члены ренты, кроме последнего, приносят проценты: на первый проценты начисляются (n-1) год, на второй — (n-2) года и т.д. На последний член проценты не начисляются.
Наращенные суммы к концу срока ренты составят:
На 1-й член 
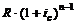
На 2-й член 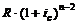
На (n-1)-й член 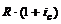
На n-й член — R
Накопленная сумма к концу срока ренты составит сумму членов этого ряда, который, если его переписать в обратном порядке, является возрастающей геометрической прогрессией, где R — 1-й член прогрессии, а величина (1 + 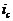 ) — знаменатель прогрессии. Сумму членов ряда, то есть наращенную сумму ренты, можно определить по формуле:
) — знаменатель прогрессии. Сумму членов ряда, то есть наращенную сумму ренты, можно определить по формуле:
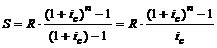 (3.1)
(3.1)
Величина 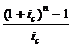 называется коэффициентом наращения ренты, который обозначим как
называется коэффициентом наращения ренты, который обозначим как 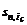 , где подстрочные символы указывают на срок ренты и применяемую процентную ставку. Тогда формула (3.1) примет вид:
, где подстрочные символы указывают на срок ренты и применяемую процентную ставку. Тогда формула (3.1) примет вид:
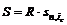 . (3.2)
. (3.2)
Значение коэффициента 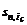 , а также значения ряда других финансовых коэффициентов, могут быть найдены из таблиц, имеющихся в любом учебном издании по финансовым вычислениям, в том числе и в данных рекомендациях. Кроме того, финансовые коэффициенты могут быть вычислены на компьютере с помощью финансовых функций, входящих в процессор Еxcel. Имеются также финансовые калькуляторы, предназначенные для проведения подобных расчетов.
, а также значения ряда других финансовых коэффициентов, могут быть найдены из таблиц, имеющихся в любом учебном издании по финансовым вычислениям, в том числе и в данных рекомендациях. Кроме того, финансовые коэффициенты могут быть вычислены на компьютере с помощью финансовых функций, входящих в процессор Еxcel. Имеются также финансовые калькуляторы, предназначенные для проведения подобных расчетов.
По данным примера 1 рассчитаем наращенную сумму ренты:
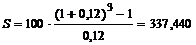 тыс. руб.
тыс. руб.
Предположим, что в примере 1 взносы будут вноситься не в конце,
а начале каждого года. В этом случае имеем ренту пренумерандо. Каждый член такой ренты «работает» на один период больше, чем в ренте постнумерандо. Отсюда наращенная сумма ренты пренумерандо, обозначим ее как 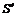 , больше в (1+
, больше в (1+ 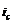 ) раз наращенной суммы аналогичной ренты постнумерандо.
) раз наращенной суммы аналогичной ренты постнумерандо.
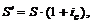 (3.3)
(3.3)
где S — наращенная сумма финансовой ренты постнумерандо.
В примере 1 для взносов в начале года наращенная сумма к концу срока ренты составит:
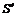 = 337,44 × (1+0,12) = 377,9328 тыс. руб.
= 337,44 × (1+0,12) = 377,9328 тыс. руб.
Нами был рассмотрен метод расчета наращенной суммы, когда рентный платеж производится один раз в году и начисление процентов также раз в году. Вместе с тем, в контрактах могут предусматриваться и другие условия поступления рентных платежей и порядок начисления процентов на них.
Рассмотрим ряд вариантов.
1) Рентные платежи вносятся один раз в году, а проценты на них начисляются m раз в году. В этом случае начисление процентов каждый раз будет производиться по ставке j/m, где j — номинальная (годовая) ставка сложных процентов.
Величина наращенной суммы ренты постнумерандо будет определяться по формуле:
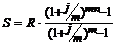 . (3.4)
. (3.4)
Величина наращенной суммы ренты пренумерандо в этом случае будет определяться по формуле:
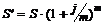 . (3.5)
. (3.5)
Пример 2.Несколько изменим условия примера 1. Пусть теперь проценты начисляются два раза в год. Рента постнумерандо.
| Имеем: j = 0,12 m = 2 R = 100 тыс. руб. n = 3 | Решение: Так как рента годовая, постнумерандо, проценты начисляются два раза в год, то наращенная сумма определяется по формуле (1.4.): |
| S=? | 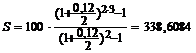 тыс. руб. тыс. руб. |
2) Рентные платежи вносятся несколько раз в году равными суммами (р-срочная рента), а начисление процентов производится один раз в конце года.
Если годовая сумма платежей равна R, то каждый раз выплачивается 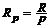 (p — количество выплат в году). Общее число членов ренты равно n × p. Ряд членов ренты постнумерандо с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен
(p — количество выплат в году). Общее число членов ренты равно n × p. Ряд членов ренты постнумерандо с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен 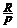 , знаменатель —
, знаменатель — 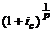 .
.
Сумма членов этой прогрессии:
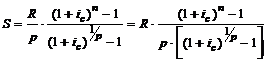 . (3.6)
. (3.6)
Наращенная сумма для ренты пренумерандо в данной ситуации будет определяться по формуле
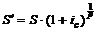 . (3.7)
. (3.7)
Пример 3. Еще раз изменим условия примера 1, допустив, что ежегодный взнос разбивается на 4 равные части, которые будут вноситься в банк в начале каждого квартала: 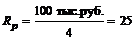 тыс. руб.
тыс. руб.
Определить накопленную сумму к концу срока ренты.
| Имеем: R = 100 тыс. руб. р = 4 ic = 0,12 n = 3 | Решение: Так как рента срочная (поквартальная), пренумерандо, проценты начисляются на платежи один раз в год, то наращенная сумма определяется по формуле (3.7.): |
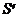 - ? - ? | 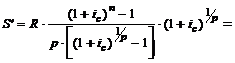 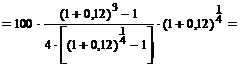 = 100362,392 тыс. руб. = 100362,392 тыс. руб. |
3) Рентные платежи вносятся несколько раз в году (р-срочная рента), число периодов начисления процентов в течение года равно числу рентных платежей (m = p).
В этом случае наращенная величина финансовой ренты постнумерандо:
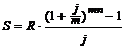 . (3.8)
. (3.8)
Наращенная сумма ренты пренумерандо:
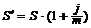 . (3.9)
. (3.9)
4) Рентные платежи вносятся р в году, начисление процентов – m раз в году; причем р 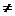 m.
m.
Наращенная сумма для ренты постнумерандо:
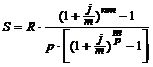 . (3.10)
. (3.10)
Наращенная сумма для ренты пренумерандо:
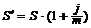
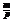 (3.11)
(3.11)
Пример 4. В условиях примера 3, допустим, что проценты на взносы будут начисляться в конце каждого полугодия. Определить наращенную сумму для ренты постнумерандо.
| Имеем: R = 100 тыс. руб. р = 4 m = 2 j = 0,12 n = 3 | Решение: Так как рента срочная (поквартальная), постнумерандо, проценты начисляются два раз в год, то наращенная сумма определяется по формуле (3.10): 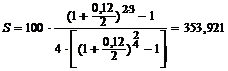 тыс. руб. тыс. руб. |
| S = ? |
Рассмотрены четыре примера определения наращенной суммы постоянной финансовой ренты. Сопоставив полученные результаты между собой, можно заметить, что величины наращенных сумм изменялись в зависимости от изменения условий ренты.
Зная, как влияют эти причины на данную характеристику финансовой ренты, целесообразно их использовать для получения наиболее выгодных условий при заключении контрактов.
Задачи для самостоятельного решения
1. Страховая компания заключила договор страхования с производственной фирмой на 4 года. Поступающие от фирмы ежегодные страховые взносы в сумме 15 тыс. руб. компания помещает в банк под 16% годовых с начислением процентов ежеквартально. Взносы производятся в начале каждого года.
Определите накопленную страховую сумму.
2. Взносы в специальный пенсионный фонд вносятся в конце каждого квартала с ежеквартальным начислением процентов по номинальной ставке 20% годовых.
Определите накопленную сумму и сумму начисленных процентов в фонде через 5 лет, если размеры очередных взносов составляют 100 рублей.
3.2. Современная величина постоянных рент постнумерандо
и пренумерандо
Современная величина находит широкое применение в разнообразных финансовых расчетах (планирование погашения долга, оценка и сравнение эффективности производственных инвестиций и т.д.).
Рассмотрение методов определения современных величин финансовых рент начнем в том же порядке, что и наращенных сумм.
Оценка современной величины производится на момент начала первого года ренты.
1) Начнем с самого простого случая — годовой ренты постнумерандо, член которой равен R, срок — n лет, годовая ставка сложных процентов — ic.
Современная величина рассчитывается по формуле:
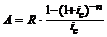 , (3.11)
, (3.11)
где величина 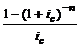 называется коэффициентом приведения ренты.
называется коэффициентом приведения ренты.
Обозначим его 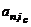 . Тогда формула (2.1) примет вид:
. Тогда формула (2.1) примет вид:
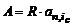 . (3.12)
. (3.12)
В Приложении 3.2 проводятся табулированные значения коэффициента приведения ренты.
Для определения современной величины ренты пренумерандо необходимо современную величину ренты постнумерандо умножить на соответствующий множитель наращения:
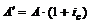 , (3.13)
, (3.13)
где 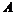 — современная величина финансовой ренты пренумерандо.
— современная величина финансовой ренты пренумерандо.
Пример 5. Фирме необходимо создать в течение трех лет фонд развития в размере 150 тыс. руб. Фирма выделяет на эти цели в конце каждого года 41,2 тыс. руб., помещая их в банк под 20% годовых (проценты сложные). Проверьте, будет ли к концу третьего года накоплена требуемая сумма.
Какая сумма потребовалась бы фирме для создания фонда в 150 руб., если бы она ее поместила в банк на три года под 20% годовых (сложные проценты)?
| Имеем: R = 41,2 тыс. руб. n = 3 ic = 0,2 | Решение: Наращенная сумма при ежегодных платежах в размере 41,2 тыс. руб. под 20 % годовых по формуле (3.1) составит: 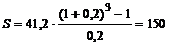 тыс. руб. тыс. руб. |
| А = ? | |
Для ответа на второй вопрос задачи найдем современную величину ренты по формуле (3.11): 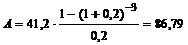 тыс. руб. Если бы фирма указанную сумму (86,79 тыс. руб.) поместила в банк на три года под 20% годовых, наращенная сумма по годовой ставке сложных процентов составила бы: тыс. руб. Если бы фирма указанную сумму (86,79 тыс. руб.) поместила в банк на три года под 20% годовых, наращенная сумма по годовой ставке сложных процентов составила бы: 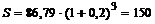 тыс. руб. тыс. руб. |
2) При начислении процентов m раз в году современная величина ренты постнумерандо вычисляется по формуле:
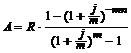 . (3.14)
. (3.14)
Современная величина финансовой ренты пренумерандо в данном случае определяется по формуле:
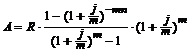 . (3.15)
. (3.15)
3) При внесении рентных платежей несколько раз в году (р-срочная рента) и начислении процентов один раз в году, современная величина ренты постнумерандо определяется по формуле:
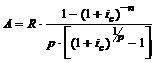 . (3.16)
. (3.16)
Современная величина финансовой ренты пренумерандо в данном случае определяется по формуле:
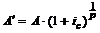 . (3.17)
. (3.17)
4) Расчет современной величины ренты постнумерандо с начислением процентов m раз в году при условии, что число рентных платежей в течение года совпадает с числом начислений процентов в течение года (m = р):
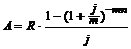 . (3.18)
. (3.18)
Современная величина финансовой ренты пренумерандо определяется по формуле:
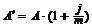 . (3.19)
. (3.19)
5) Расчет современной величины ренты постнумерандо с начислением процентов m раз в году при условии, что число рентных платежей в течение года не равно числу периодов начисления процентов (р ¹ m):
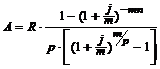 . (3.20)
. (3.20)
Современная величина финансовой ренты пренумерандо определяется по формуле:
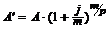 . (3.21)
. (3.21)
Задачи для самостоятельного решения
3. Определите современную величину ренты, если платежи вносятся в течение 4 лет в конце каждого года в размере 90 тыс. руб. и на них в конце каждого полугодия начисляются проценты по ставке 10% годовых.
4. Годовой платеж в сумме 400 тыс. руб. вносится два раза в год (в начале каждого полугодия) равными частями в течение 3 лет. Проценты начисляются четыре раза в год по ставке 20% годовых.
Определите современную величину финансовой ренты.
