Финансово-экономический анализ инвестиционных проектов при помощи программы mathcad
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ АНАЛИЗ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ ПРИ ПОМОЩИ ПРОГРАММЫ MATHCAD
Андрусевич В.В.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ................................................................................................................................... 3
1. УНИВЕРСАЛЬНАЯ СИСТЕМА КОМПЬЮТЕРНОЙ МАТЕМАТИКИ MATHCAD.... 4
1.1. МАТЕМАТИЧЕСКИЙ АРСЕНАЛ ПРОГРАММЫ MATHCAD 4
1.2. ИНТЕРФЕЙС MATHCAD 5
1.3. ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ И ФИНАНСОВЫЕ ФУНКЦИИ MATHCAD 7
2. ОСНОВНЫЕ ПРИЕМЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ................... 11
2.1. ПРОСТЫЕ ПРОЦЕНТЫ 11
2.2. СЛОЖНЫЕ ПРОЦЕНТЫ (КОМПАУНДИНГ) 13
2.3. МЕТОД ДИСКОНТИРОВАНИЯ 16
2.4. СТАНДАРТНЫЙ АННУИТЕТ 18
2.5. ТЕКУЩИЙ АННУИТЕТ 20
2.6. ЧИСТОЕ ПРИВЕДЕННОЕ ЗНАЧЕНИЕ ФИНАНСОВОГО ПОТОКА 22
2.7. БУДУЩЕЕ ПРИВЕДЕННОЕ ЗНАЧЕНИЕ 23
2.8. ВНУТРЕННЯЯ ДОХОДНОСТЬ ПОТОКА ПЛАТЕЖЕЙ 24
3. ПРИМЕРЫ РАСЧЕТОВ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ........................................ 26
3.1. МЕТОД КОМПАУНДИНГА 26
3.2. МЕТОД ДИСКОНТИРОВАНИЯ 28
3.3. МЕТОД СТАНДАРТНОГО АННУИТЕТА 30
3.4. ТЕКУЩИЙ АННУИТЕТ, ЧИСТЫЙ ПРИВЕДЕННЫЙ ДОХОД, КУМУЛЯТИВНЫЙ ДОХОД ИНВЕСТИЦИОННОГО ПРОЕКТА 33
3.5. ВНУТРЕННЯЯ ДОХОДНОСТЬ ИНВЕСТИЦИОННОГО ПРОЕКТА 35
4. КРИТЕРИИ ОЦЕНКИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ........................................... 36
4.1. ЧИСТЫЙ ПРИВЕДЕННЙ ЭФФЕКТ 36
4.2. ИНДЕКС РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ 37
4.3. НОРМЫ РЕНТАБЕЛЬНОСТИ ИНВЕСТИЦИЙ 37
4.4. СРОК ОКУПАЕМОСТИ ИНВЕСТИЦИЙ 37
4.5. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА ПО СОВОКУПНОСТИ КРИТЕРИЕВ 38
4.6. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОГО ПРОЕКТА В УСЛОВИЯХ ИНФЛЯЦИИ 39
5. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ............................ 40
5.1. РАСЧЕТ ОЦЕНОК ЭФФЕКТИВНОСТИ ПЕРВОГО ПРОЕКТА 40
5.2. РАСЧЕТ ОЦЕНОК ЭФФЕКТИВНОСТИ ВТОРОГО ПРОЕКТА 42
5.3. РАСЧЕТ ОЦЕНОК ЭФФЕКТИВНОСТИ ТРЕТЬЕГО ПРОЕКТА 43
5.4. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ПРОЕКТОВ 46
ЛИТЕРАТУРА............................................................................................................................. 47
ВВЕДЕНИЕ
Оснащение высшей школы персональными компьютерами и современным программным обеспечением позволяет по-новому проводить процесс изучения многих дисциплин, в особенности тех, в основе которых лежит математика. Пакеты прикладных программ типа Mathcad, Excel и др. дают возможность на практических занятиях переложить рутинные вычисления на долю компьютера (хотя нельзя оспорить пользу для понимания предмета и рутинных «ручных» вычислений), существенно увеличить размерность и количество рассматриваемых задач и эффективно заниматься проверкой и использованием теоретических результатов, рассмотренных на лекционных занятиях. Программные пакеты можно использовать при изучении курсов «Информационные технологии управления», «Математические методы оптимизации и экономическая теория», «Экономико-математические методы и прикладные модели» и т.д.
При поддержке принятия решений наиболее часто используются технологии аналитического моделирования: оптимизационный анализ, анализ чувствительности, корреляционно-регрессионный анализ, анализ и прогнозирование на основе трендов, финансовый анализ.
Оптимизационный анализ или анализ целевой функции широко применяется при поиске, например, оптимальной цены или оптимальных объемов продаж конкретного товара при заданной цене и издержках.
Технология корреляционно-регрессионного анализа может помочь менеджеру в проверке некоторых гипотез относительно существования связей между зависимыми переменными и факторами, а также при поиске статистически значимых моделей для целей объяснения, предсказания и управления. Эта технология применяется для маркетингового и финансового менеджмента, а также для управления качеством продукции. Средства такого анализа содержатся в Mathcad, электронных таблицах Excel и в других прикладных программах, например, в статистическом пакете SPSS.
Технология анализа и прогнозирования на основе трендов, то есть анализа динамики различных показателей с использованием графического и математического моделирования является повседневным орудием маркетолога и может быть использована в СППР для анализа новых данных.
Финансовый анализ является наиболее важным элементом управления предприятием и основой финансового менеджмента и аудита. Практически все пользователи финансовых отчетов предприятий используют методы финансового анализа для принятия решений по оптимизации своих интересов.
Mathcad позволяет автоматизировать решение перечисленных задач, в том числе, задач финансового анализа.
В данной лекции приведены простые модельные примеры решения и исследования задач анализа финансовых потоков и финансового анализа инвестиционных проектов. Подобные задачи финансовой математики входят в качестве составной части в курс информационных технологий управления [11 - 14].
ИНТЕРФЕЙС MATHCAD
Внимательное рассмотрение представленного выше «экрана» позволяет также сэкономить много времени, требующегося для первоначального знакомства с интерфейсом программы. Легко заметить, что Mathcad является типичной программой «под Windows» со стандартным меню, панелями инструментов, элементами управления и т.п. Нет необходимости в этой лекции рассматривать все эти элементы подробно. Остановимся только на двух группах из них.
Сначала приведем «экран», заполненный набором палитр математических символов и операций, названия которых и пиктограммы кнопок сами за себя говорят многое об их предназначении, пользователю программы, знакомому с математикой (а на других программа и не рассчитана). Каждая палитра «включается» и «выключается» с помощью кнопок панели инструментов, пронумерованных на рабочем листе цифрами от 1 до 9. Все эти палитры можно также активизировать через меню View – Toolbars., а также обычным способом с помощью мыши перенести любую из них и «вмонтировать» ниже или рядом со стандартной панелью инструментов и панелью форматирования (см. дальнейшие изображения).
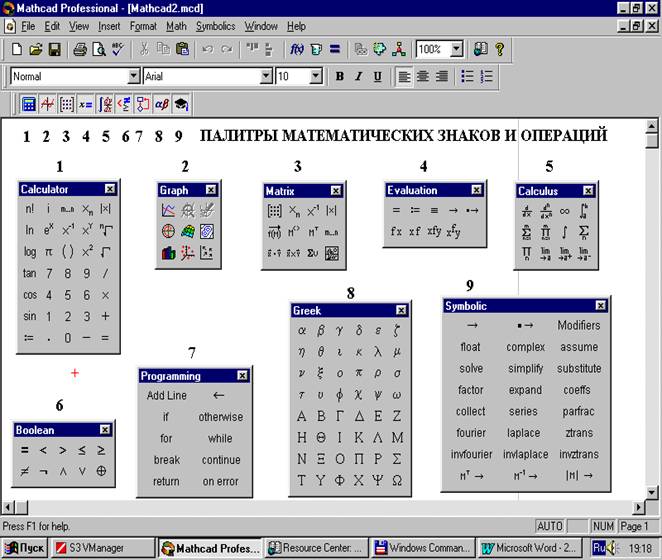
Приведем также изображения содержимого нескольких элементов главного меню, имеющих отношение к математической составляющей программы, и тем самым отличающихся от стандартных пунктов меню программы «под Windows».
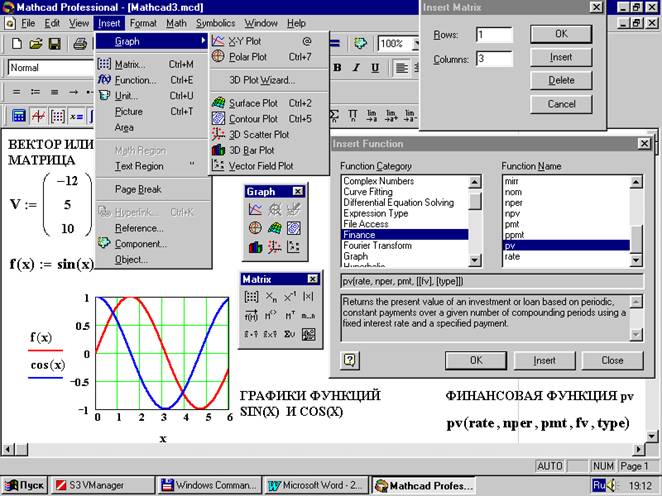
На помещенном ниже изображении представлено содержимое пункта меню Insert(Вставить, ввести) и подменю Graph (График) целым набором команд для построения и исследования графиков. После Graph в меню Insert следуют пункты меню Matrix и Function. Все три указанных пункта меню или соответствующие кнопки панели инструментов палитр понадобятся в дальнейшем. На рабочем листе помещены также палитра Matrix и палитра Graph, с набором кнопок, дублирующих команды подменю Graph, диалоговое окно Insert Matrix с полями ввода для числа строк и столбцов матрицы (вектора) и диалоговое окно Insert Function со списками встроенных функций Mathcad, разбитых на отдельные категории, в том числе финансовых функций. На рабочем листе представлены необходимые элементы интерфейса для ввода вектора (матрицы), функции, построения графика функции. Примеры перечисленных математических объектов помещены на рабочий лист с пояснениями. Введен вектор V размерами 1х3, функции sin(x), cos(x) (введена непосредственно в шаблон графика) и финансовая функция с пятью аргументами, на одних осях координат построены двумя разными способами построены графики функций sin(x) и cos(x). Аналогичные операции потребуются при финансовых вычислениях и анализе инвестиционных проектов, поэтому и упоминаются сейчас. Более подробно об этом будет сказано при решении конкретных задач.
ПРОСТЫЕ ПРОЦЕНТЫ
Рассмотрим схему предоставления некоторой суммы денег P в кредит на время t. За использование кредита надо платить, поэтому возвращаемая сумма составит величину S = P + I. Плату за кредит I часто называют «процентом» (interest). Чем больше время, на которое выдается кредит, тем больше процент. В простейшем случае плата за кредит I = Prt, где r – плата за кредит в единицу времени. Время t измеряется в днях, месяцах, кварталах, годах. Процентная ставка r (rate of interest) измеряется в процентах, разделенных на единицу времени, например, в проц./год.
Таким образом, величина наращиваемой суммы определяется по формуле
(1) S = P(1 + rt).
Если t = 1 год, то S = P(1 + r). Отношение S/P называется коэффициентом наращения.
Вычисления для простых процентов по приведенной формуле производятся следующим образом. Заданы сумма кредита P, ставка процента r и срок t, на который предоставляется кредит. Прежде всего надо проследить и при необходимости скорректировать размерности данных. Если, например, задана годовая процентная ставка r, а срок кредита исчисляется в днях, то срок кредита нужно выразить в долях года: t = n/N, где N – число дней в году, или временная база. Рассмотрим конкретный пример.
ЗАДАЧА 1. Выдан кредит в размере P = 1 млн. рублей при годовой процентной ставке r = 20%. Какую сумму S потребуется вернуть, если кредит выдан на 3 месяца, 6 месяцев, 1 год, 2 года, …, 5 лет под простой процент.
Решение. Годовая процентная ставка равна r = 20% = 0.2. Сроки кредита выразим в долях года t = 3/12 = 0.25 года, 6/12 = 0.5 года, 1, 2, 3, 4 года, 5 лет. Вычисляя формуле (1), получаем для трехмесячного кредита, выданного под простой процент, сумма S = 1х(1 + 0.2х0.25) = 1.05 млн. руб. Для шестимесячного кредита возвращаемая сумма составит 1.1 млн. руб. Для кредитов, предоставленных на 1 год, 2 года, …, 5 лет возвращаемые суммы составят 1.2, 1.4, 1.6, 1.8 и 2 млн. руб.
Хотя приведенная задача элементарно решается «вручную», приведем ее решение в Mathcad. На рабочем листа зададим сначала сумму кредита P, процентную ставку r , формулу (1) в виде функции S(t) и сроки кредита t в долях года. Для демонстрации разнообразия способов выдачи результатов вычислим сначала возвращаемые суммы для трехмесячного и шестимесячного кредитов по отдельности. Затем зададим сроки кредита в виде ранговой переменной t := 0..5 выведем вычисленные результаты в виде двух табличек t = и S(t) = . Кроме того, построим график зависимости возвращаемой суммы от срока кредита. Для этого введем на рабочий лист шаблон двумерного декартового графика (меню View – Toolbars – палитра Graph).

Затем в шаблоне графика назначим ось абсцисс как ось переменной t, а ось ординат – ось функции S(t). Отредактируем график (масштаб, оси, координатная сетка и т.п.). Получим следующие результаты.

В международных стандарте, а также в Mathcad принята несколько иная форма записи финансовых формул, в том числе формулы (1). Вместо P используется PV (Present Value) – настоящая величина, текущая величина капитала, а вместо пишут FV (Future Value) – будущая величина капитала. Кроме того, сумма инвестиций (кредита) и возвращаемая сумма, как правило, записываются с разными знаками: знак минус соответствует случаю, когда Вы (или рассматриваемое лицо) даете деньги, а знак плюс, когда Вы их получаете. В соответствии с этим стандартом формула (1) примет вид
(1) FV + PV(1 + rt) = 0 или FV = - PV(1 + rt).
СЛОЖНЫЕ ПРОЦЕНТЫ (КОМПАУНДИНГ)
Суть компаундинга или роста по правилу сложных процентов состоит в определении суммы денег, которую будет иметь инвестор в конце операции по истечении ее срока. При использовании этого приема исследование финансового потока ведется от настоящего к будущему. Заданными величинами являются базовая (текущая, сегодняшняя) сумма капитала PV (Present Value), процентная ставка доходности r (rate) в десятичном выражении (10% = 0.1), число n периодов (например, лет) или срок, на который капитал инвестируется.
По методу сложных процентов будущий доход FV (Future Value) рассчитывается по формуле
(2) FV = - PV (1 + r)n.
Величина R(r,n)=(1 + r)nназывается коэффициентом сложных процентов.
В более общем случае, когда наряду с годовой процентной ставкой имеет место m начислений процентов в течение года формула для сложных процентов принимает вид
(3) FV = - PV (1 + r/m)nm.
Это означает, что базовый период составляет год, деленный на количество начислений, а ставка сложных процентов для периода равна r/m. При этом число периодов увеличивается в m раз.
Ниже приведена таблица этих коэффициентов для различных r от 1% до 15% и n от 1 до 10, рассчитанная в Mathcad.
Таблица 1.
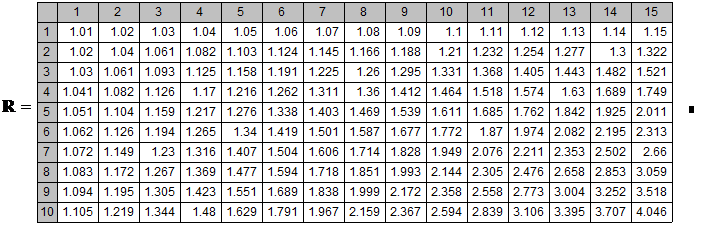
От периода к периоду базовая сумма, на которую начисляется процент, возрастает. Поэтому инвестор имеет доход как с первоначального капитала, так и с процентов, полученных за предыдущие периоды.
Приведем пример вычисления сложных процентов и построим график роста капитала для этого примера. Пусть первоначальный капитал PV=10 млн. руб., процентная ставка r=20%, время (число периодов) n меняется от 0 до 10. В таблице и на графике показан рост капитала.
МЕТОД ДИСКОНТИРОВАНИЯ
Метод дисконтирования денежных поступлений есть исследование денежного потока от будущего к текущему моменту. Другими словами, метод дисконтирования является обратным к методу компаундинга и состоит в приведении будущих доходов к сегодняшнему моменту времени. Он позволяет определить, сколько денег нужно вложить сегодня, чтобы получить определенную сумму через несколько периодов. Формула для метода дисконтирования является обратной к формуле компаундинга:
(4) PV = - FV / (1 + r)n.
Величины D(r,n)=1/(1 + r)n называются коэффициентами дисконтирования. Ниже приведена таблица этих коэффициентов для различных r от 1% до 15% и n от 1 до 10.
КОЭФФИЦИЕНТЫ ДИСКОНТИРОВАНИЯ
Таблица 2.
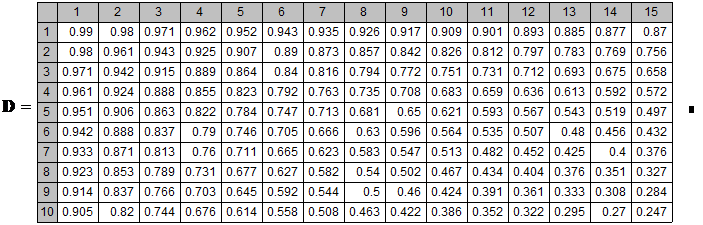
Приведем пример использования метода дисконтирования для вычисления начальных инвестиций и построим соответствующий график в Mathcad. Пусть инвестор через несколько лет хочет получить капитал FV=25.907 млн. руб., при процентной ставке r=8%. График зависимости PV (без учета знака) от времени n (число периодов n меняется от 0 до 10) показывает, сколько ему следует инвестировать сегодня для получения указанной суммы через n периодов (лет).
ВЫЧИСЛЕНИЕ НАЧАЛЬНЫХ ИНВЕСТИЦИЙ
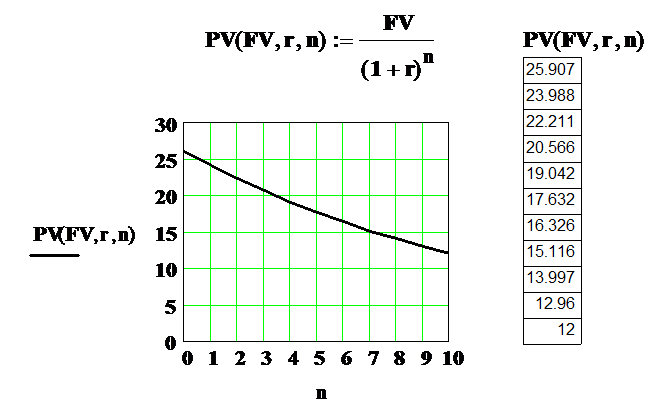
Также как и для вычисления сложных процентов начиная с версии Mathcad 2000 нет необходимости выписывать формулу для вычисления начальных вложений в явном виде. Среди набора финансовых функций имеется функция pv, действующая в соответствии со следующим синтаксисом
pv(rate, nper, pmt, [[fv], [type]]).
Устроена она совершенно аналогично с функцией fv, с той лишь разницей, что fv и pv меняются местами. Пример вычислений начальных инвестиций pv при заданной будущей возвращаемой сумме fv, процентной ставке за период rate и числу периодов nper приведен ниже. Там же построен график зависимости исходной суммы от срока вложений n, меняющегося от 1 до 10. Вычисления проведены с учетом знаков.
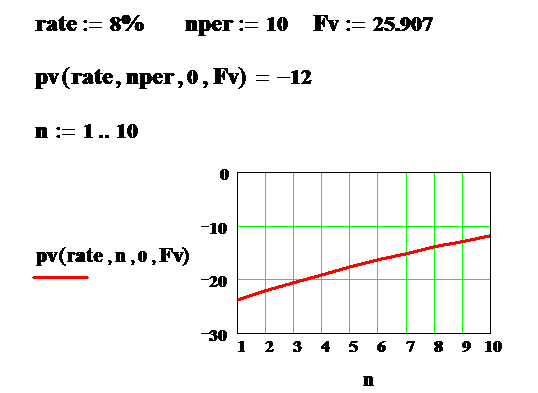 |
СТАНДАРТНЫЙ АННУИТЕТ
До сих пор мы рассматривали простейший финансовые потоки вида {- PV, FV } или { PV, - FV } с однократными взносами и выплатами. Однако не менее распространенными являются схемы денежных потоков с многократными взносами и выплатами через равные промежутки времени. Поток платежей { -PV, PMT, PMT,…, PMT, FV },все составляющие которого, кроме первого и последнего, имеют одинаковую величину и разделены равными промежутками времени, называется постоянной рентой. Формулу, приводящую все платежи к будущему, называют стандартным или будущим аннуитетом. Стандартный аннуитет основан на сложных процентах. Формула стандартного аннуитета имеет следующий вид:
(5) FVAn,r = PMT ´ AFn,r = PMT ´ [(1 + r)n -1]/r.
Если учесть первоначальный взнос, то конечная возвращаемая сумма будет равной
(6) FVn,r = -PV(1+r)n + FVAn,r = -PV(1+r)n + PMT ´ [(1 + r)n -1]/r.
Величина FVAnназывается будущей стоимостью аннуитета. Величина PMT- разовый платеж в конце периода n. Коэффициенты AFnr– будущая стоимость аннуитета в 1 рубль в конце каждого периода n при процентной ставке r.
Происхождение формулы легко понять, если сложить коэффициенты сложных процентов, начиная от 0 до n-1 включительно. Действительно, сумма коэффициентов сложных процентов за n периодов равна следующей геометрической прогрессии:
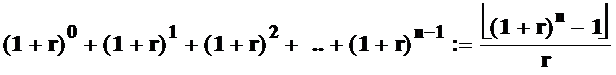
Приведем таблицу коэффициентов стандартного (будущего) аннуитета для n от 1 до 6 и r от 5% до 15%.
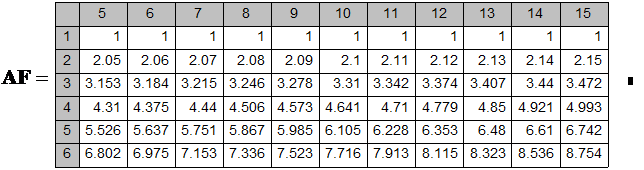
КОЭФФИЦИЕНТЫ БУДУЩЕГО АННУИТЕТА
Таблица 3.
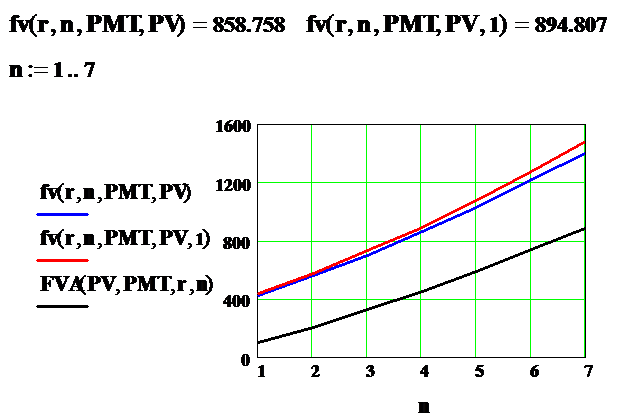
Приведем пример вычисления по формулам будущего аннуитета. Первоначальный взнос составляет 300 денежных единиц, а затем 4 периода подряд вносится по 100. Процентная ставка – 8%. Накопленная сумма составит 858.758.

Вычислим величину будущих накоплений с помощью финансовой функции fvпрограммы Mathcad для счета постнумерандо (взнос в конце периода, пятый аргумент type функции fv равен 0 или опущен) и для счета пренумерандо (взнос в начале периода, пятый аргумент функции fv равен 1). Построим также графики роста накопленной суммы как функции количества периодов n для обоих случаев, а также график роста чистого будущего аннуитета FVA (нулевой начальный взнос PV=0).
ТЕКУЩИЙ АННУИТЕТ
Текущий аннуитет основан на дисконтировании и определяет сумму взносов (выплат, платежей), приведенную к настоящему времени с учетом процентной ставки. Формулы для вычисления текущего аннуитета имеет следующий вид:
(7) PVAn,r = PMT ´ APn,r = PMT ´ [1-1/(1 + r)n]/r.
(8) PVn,r = PV + PVAn,r = PV + PMT ´ [(1 + r)n -1]/r.
Величина PVAn,r – текущая стоимость будущих денежных поступлений при величине процентной ставки r, величине периодических платежей PMT и количестве периодов n. Формула (8) определяет приведенную сумму с учетом начальной суммы PV.
Коэффициенты APn,r = [1-1/(1 + r)n]/r – текущая стоимость аннуитета в 1 рубль в конце каждого периода n при ставке дохода r.
Эти коэффициенты являются суммами коэффициентов дисконтирования. Действительно, сумма коэффициентов дисконтирования за n периодов равна сумме следующей геометрической прогрессии:
 |
Коэффициенты текущего аннуитета для n от 1 до 6 и r от 5% до 15% представлены в таблице 4.
КОЭФФИЦИЕНТЫ ТЕКУЩЕГО АННУИТЕТА
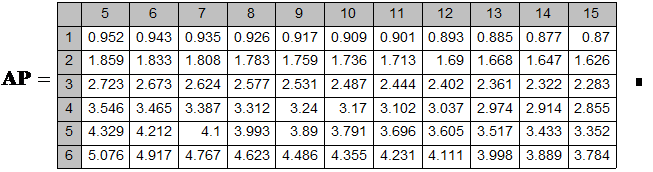
Таблица 4
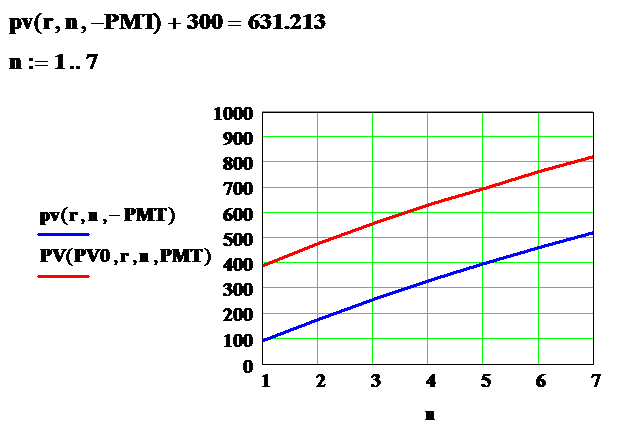
Рассмотрим тот же, что и в предыдущем пункте с точки зрения текущего аннуитета. Напомним, что первоначальный взнос составляет 300 денежных единиц, а затем 4 периода подряд вносится по 100. Процентная ставка – 8%. Накопленная сумма в соответствии со стандартным аннуитетом составила 858.758. Однако, эта же сумма, приведенная к настоящему времени, что видно из представленных вычислений составит всего 631.213 денежных единиц.
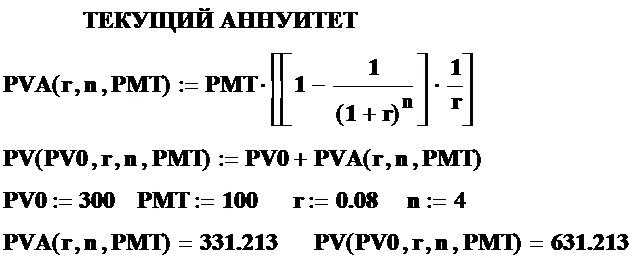
Вычисления будущего аннуитета с помощью финансовой функции pv программы Mathcad дают тот же результат, если учесть, что периодические взносы PMT должны быть подставлены в эту функцию со знаком минус. На графике приведены зависимости приведенной общей суммы накоплений и текущего аннуитета от количества периодов n, вычисленные по формуле и посредством использования финансовой функции pv.
ПРИМЕРЫ РАСЧЕТОВ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ
МЕТОД КОМПАУНДИНГА
Рассмотрим пример сравнительной оценки инвестиционных проектов на основе компаундинга. Пусть имеется два альтернативных проекта со сроком окупаемости 5 лет. Проект А дает одинаковые доходы по годам, а проект Б требует вложений в первые годы, но дает большую отдачу в последующие годы. Размеры чистого дохода по годам обоих проектов приведены в таблице 5.
Таблица 5
| Годы | Проект А | Проект Б |
| -110 | ||
| Всего |
Если сравнивать только суммы чистого дохода за 5 лет без учета сроков их получения, то более выгодным является проект Б.
Оценим теперь эти проекты с учетом того, что полученный доход можно пустить в рост под некоторый альтернативный процент по схеме сложных процентов. Аналогично можно было бы поступить и со средствами, которые инвестируются в проект Б. Суммы чистых доходов и их стоимость, приведенная ко времени окончания проектов, а также коэффициенты сложных процентов по годам приведены в таблице 6.
Таблица 6
| Годы | Проект А Чистый доход | Проект А Стоимость через 5 лет | Коэффициент сложных процентов r = 10% | Проект Б Чистый доход | Проект Б Стоимость через 5 лет |
| 219.62 | (1+0.1)4=1.464 | -110 | -161.05 | ||
| 199.65 | (1+0.1)3=1.331 | 93.07 | |||
| 181.50 | (1+0.1)2=1.210 | 193.60 | |||
| 165.00 | (1+0.1)1=1.100 | 418.00 | |||
| 150.00 | 1.000 | 300.00 | |||
| Всего | 915.77 | 6.105 | 843.72 |
Проект А с учетом использования получаемых доходов через 5 лед принесет в сумме 915.00 тыс. руб., что больше аналогичной стоимости проекта Б, которая равна 843.72 тыс. руб. Проект А более выгоден.
Решим эту же задачу с помощью программы Mathcad. Введем на рабочий лист процентную ставку, число лет от 1 до 5, векторы доходов и инвестиций обоих проектов и формулу для вычисления сложных процентов в обратной перспективе. Подставим в эту формулу оба вектора и получим таблички вычисленных доходов по правилу сложных процентов по годам.
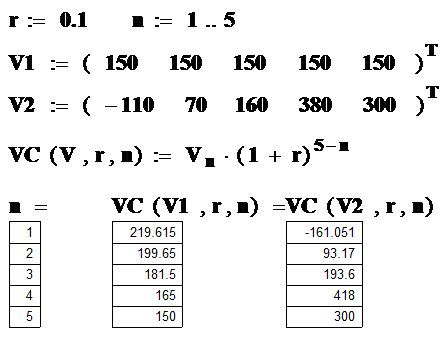 |
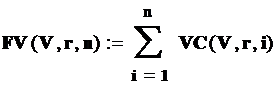 |
Рассчитаем суммы доходов нарастающим итогом для обоих проектов по формуле
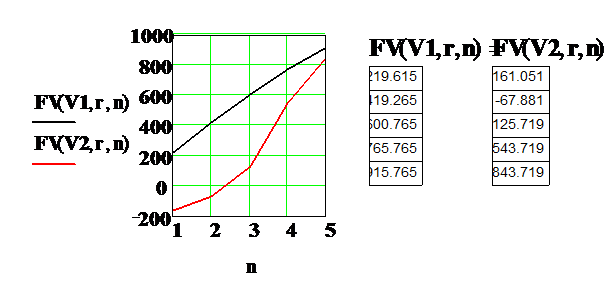
Приведем полученные результаты и построим графики для этих сумм.
Суммарный доход для каждого проекта можно вычислить с помощью финансовой функции fvc. Смысл аргументов и синтаксис функции понятен из приведенных формул. Наблюдаем полное совпадение результатов во всех трех вариантах вычислений.
 |
МЕТОД ДИСКОНТИРОВАНИЯ
При оценке инвестиционного проекта в качестве альтернативной процентной ставки, то есть ставки, с которой сравнивают данный инвестиционный проект, принимается ставка банковского процента по депозитам или процент по государственным обязательствам плюс, как правило, надбавка за риск. Эта надбавка может учитывать как риски, связанные с самим проектом, так и риски, обусловленные, например, общей неблагоприятной экономической или политической обстановкой (значительной инфляцией, политической нестабильностью и т.п.).
Рассмотрим пример применения метода дисконтирования для оценки эффективности инвестиционного проекта. Пусть имеется начальный капитал 1000 тыс. руб. Инвестирование его в проект при сроке реализации 4 года дает ежегодный доход 300 тыс. руб. Рассчитаем чистую текущую стоимость доходов, используя коэффициенты дисконтирования (таблица 5).
Таблица 5
| Годы | Доход | Коэффициенты дисконтирования | PV | ||
| при r1=10% | при r2=6% | 10% | 6% | ||
| - | 1.000 | 1.000 | - | - | |
| 0.9091 | 0.9434 | 272.37 | 283.02 | ||
| 0.8264 | 0.8900 | 247.92 | 267.00 | ||
| 0.7513 | 0.8396 | 225.40 | 251.88 | ||
| 0.6830 | 0.7921 | 204.92 | 237.62 | ||
| Всего | - | - | 950.96 | 1039.48 |
Из таблицы следует, что при альтернативной процентной ставке 10% проект оказывается неэффективным, так как приведенная к настоящему времени сумма будущих доходов PV=950.96 тыс. руб. меньше требуемых инвестиций. Более выгодным проектом будет помещение капитала на депозит. Если же процентная ставка равна 6%, то приведение будущих доходов по проекту к настоящему времени дает PV=1039.48 тыс. руб., что несколько превышает инвестируемую сумму. Если не учитывать риски (инфляция и др.), то есть смысл инвестировать. Таким образом, оказывается, что выгодность или невыгодность одного и того же проекта зависит от внешних по отношению к проекту факторов.
Проанализируем предлагаемый инвестиционный проект с помощью программы Mathcad. Введем на рабочий лист объем инвестиций I, процентные ставки r1 и r2, число лет n от 1 до 4, величину ежегодного дохода P и формулу для вычисления ежегодного приведенного дохода PD(P,r,n) как функцию P, r и n. Подставим в эту формулу оба значения процентной ставки и получим таблички приведенных доходов по годам по
 |
методу дисконтирования. Получим результаты, совпадающие с предыдущими вычислениями
Поставим задачу определения значений параметров задачи при которых проект становится выгодным. Для этого проекта изменим число лет n от 1 до 5 и вычислим сумму PV(P, r, n) приведенных доходов нарастающим итогом и вычислим эти суммы для обеих процентных ставок.
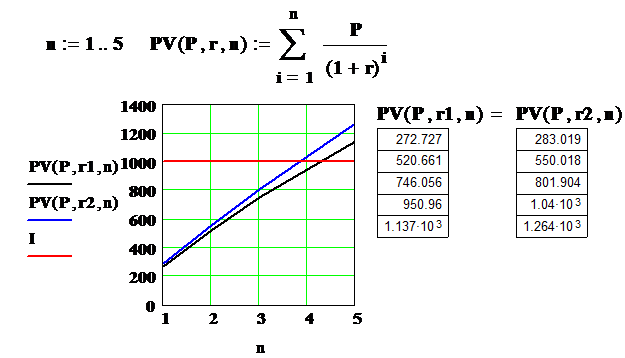
Из полученных данных, представленных в графической и табличной форме, следует, что при ставке r2 = 6% проект выгоден, а при ставке r1 = 10% сумма приведенных доходов меньше суммы инвестиций. При этой ставке приведенные доходы превысят инвестиции только за 5 лет.
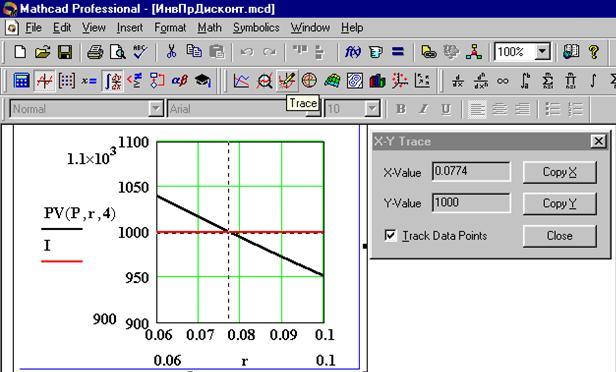
Определим графическим способом предельную процентную ставку, при которой инвестиции оправдают себя за 4 года. Для этого построим график PV(P, r, 4), как функции аргумента r. Подберем приемлемые интервалы изменения функции и масштабы графика по обеим осям. Затем воспользуемся дополнительной возможностью, имеющейся в программе Mathcad для графического анализа, – трассировкой графиков. Активизируем построенный график щелчком мыши и нажмем кнопку Trace в палитре Graph. На экране появится диалоговое окноX-Y Trace. Щелкнем снова на графике, после чего на нем появятся вертикальная и горизонтальная перекрещивающиеся пунктирные линии. Координаты пересечения этих линий отражены в окошках X-Value и Y-Value диалогового окнаX-Y Trace. Для того чтобы перекрестье автоматически отслеживало линию графика, поставим флажок в окошке Track Data Points. Переместим мышью перекрестье так, чтобы оно совпало с пересечением линий графика функции PV(P, r, 4) и горизонтальной линии I = 1000. Точность совпадения с последней контролируем по показанию окошка Y-Value (Y = 1000). В окошке читаем значение искомой предельной процентной ставки r = 0.0774 = 7.74%.
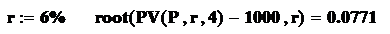 |
Более точное значение предельной процентной ставки можно получить, решив уравнение PV(P, r, 4) – 1000 = 0 относительно неизвестной r с помощью функции root (корень).
ЧИСТЫЙ ПРИВЕДЕННЙ ЭФФЕКТ
Чистый приведенный эффект или метод чистой текущей стоимости основан на сопоставлении исходных инвестиций с общей суммой дисконтированных денежных поступлений, полученных в течение выполнения инвестиционного проекта. При применении этого метода сначала определяется стоимость инвестиционных затрат IC. Затем рассчитывается стоимость будущих денежных поступлений от проекта PV , приведенных к определенной дате. Последний расчет показывает, сколько средств нужно было бы вложить сегодня для получения запланированных доходов, если бы ставка доходов была равна ставке процента в банке. Текущая стоимость доходов сравнивается с текущей стоимостью затрат.
Таким образом, общая сумма дисконтированных поступлений определяется по формуле
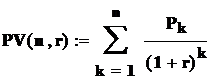 |
где Pk– годовые доходы в каждомk-ом периоде,n– число лет реализации проекта,r– базовая процентная ставка.
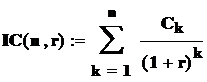 |
В общем случае, если затраты на осуществление проекта не являются разовыми, а распределены во времени, по тому же правилу вычисляется приведенная текущая стоимость затрат
где Ck– затраты в каждомk-ом периоде.
Чистый приведенный эффект или чистая текущая стоимость проекта равна разности между приведенными доходами и затратами:
NPV = PV – IC.
Если NPV>0, то есть PV>IC, то проект принимается. Если NPV<0, то есть PV<IC, то проект отвергается. Если NPV=0, то есть PV=IC, то ситуация не определена и для оценки проекта требуются другие критерии.
Критерий чистой текущей стоимости является одним из основных в оценке инвестиционных проектов по следующим причинам. Во-первых, с его помощью можно определить изменение экономического потенциала предприятия. Во-вторых, используя его можно дать совокупную оценку одновременного осуществления нескольких инвестиционных проектов.
СРОК ОКУПАЕМОСТИ ИНВЕСТИЦИЙ
Алгоритмы расчета зависят от равномерности распределения доходов по годам прогнозируемого периода. Если доходы по годам распределены равномерно, то срок окупаемости определяется делением единовременных вложений на величину годового дохода. Если доходы по годам распределены неравномерно, то срок окупаемости рассчитывается прямым подсчетом числа лет, в течение которых исходные инвестиции будут погашены кумулятивным (накопленным) доходом.
Формула для расчета этого критерия есть
PP = min n,при которомP1 + P2 + … + Pn ³ IC.
Приведем простой пример. Пусть инвестиции составили 10 млн. рублей, а ежегодный доход составляет 2.5 млн. рублей. Тогда срок окупаемости равен 10/2.5 = 4 года.
Пример неравномерных доходов. Пусть инвестиции составили 12 млн. рублей, а доходы по годам распределены следующим образом: 3, 4, 5, 4. Тогда срок окупаемости составит 3 года, так как 3+4+5=12.
Этот критерий является самым простым, самым распространенным и самым неверным. Прежде всего, он не учитывает доходы, получаемые после истечения срока окупаемости. Сравним два инвестиционных проекта с одинаковыми вложениями 12 млн. рублей. Пусть доходы по годам в первом проекте составляют 3, 4, 5, 1, 1, 1 млн. рублей, а во втором в первом проекте 3, 4, 5, 4, 3, 2 млн. рублей. Срок окупаемости обоих проектов составляет 3 года, то есть по этому критерию проекты одинаковы, что неверно.
Во-вторых, этот критерий не делает различий между проектами с одинаковой суммой доходов, но с различным распределением их по годам. Например, два проекта (-12, 3, 4, 5) и (-12, 5, 4, 3) по сроку окупаемости совершенно одинаковы, но по другим критериям, учитывающим различную стоимость денег по годам очевидна предпочтительность второго проекта.
Кроме того, используя срок окупаемости в качестве критерия, нельзя рассчитать общий срок окупаемости при одновременном осуществлении ряда проектов.
Поэтому этот критерий применим только для первоначальной отбраковки заведомо неприемлемых проектов, а также при оценке проектов в условиях значительных инфляции и рисков.
Таблица 6
| Год | Денежные поступления за год | Коэффициент дисконтирования | Текущая стоимость дохода | Чистая текущая стоимость | |
| За год | Текущий аннуитет | ||||
| - 360 | 1.000 | - | - | -360.00 | |
| 0.909 | 0.909 | 181.8 | -178.2 | ||
| 0.826 | 1.735 | 132.2 | -46.0 | ||
| 0.751 | 2.486 | 90.2 | +44.2 | ||
| Всего | 404.2 |
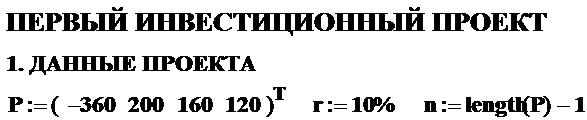 |
Вычислим все показатели первого инвестиционного проекта с помощью программы Mathcad. Введем сначала данные проекта.
Определим затем все показатели первого инвестиционного проекта, пользуясь рассмотренными ранее методами.
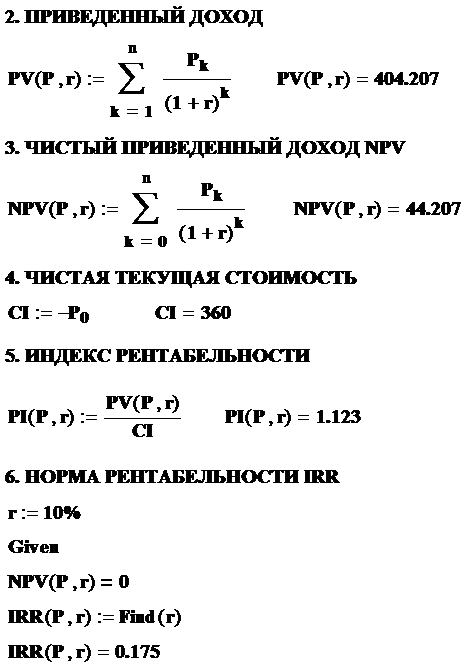 |
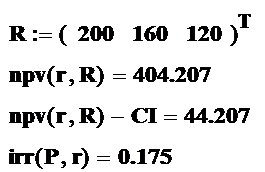 |
Рассчитаем также соответствующие показатели с помощью встроенных финансовых функций, имеющихся в версии Mathcad 2000 и далее.
Таблица 7
| Год | Денежные поступления за год | Коэффициент дисконтирования | Текущая итоговая стоимость дохода | Чистая текущая стоимость | |
| За год | Текущий аннуитет | ||||
| - 500 | 1.000 | - | - | -500.00 | |
| 0.909 | 0.909 | 118.2 | -381.8 | ||
| 0.826 | 1.735 | 225.6 | -274.4 | ||
| 0.751 | 2.486 | 323.2 | -176.8 | ||
| 0.683 | 3.169 | 412.0 | -88.0 | ||
| 0.621 | 3.790 | 492.7 | -7.3 | ||
| 0.565 | 4.355 | 566.2 | +66.2 |
Вычислим показатели второго инвестиционного проекта с помощью программы Mathcad. Введем данные проекта. Определим затем все показатели второго инвестиционного проекта, пользуясь рассмотренными ранее методами.

 |
Рассчитаем также соответствующие показатели с помощью встроенных финансовых функций.
 |
Таблица 8
| Год | Денежные поступления за год | Коэффициент дисконтирования | Текущая итоговая стоимость дохода | Чистая текущая стоимость | |
| За год | Аннуитет | ||||
| - 400 | 1.000 | - | - | -400.00 | |
| 0.909 | 0.909 | 90.9 | -309.1 | ||
| 0.826 | 1.735 | 173.5 | -226.5 | ||
| 0.751 | 2.486 | 248.6 | -151.4 | ||
| 0.683 | 3.169 | 316.9 | -83.1 | ||
| 0.621 | 3.790 | 379.1 | -20.9 | ||
| 0.565 | 4.355 | 435.6 | +35.4 Наши рекомендации
|
