Основные характеристики инвестиционных портфелей

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИНВЕСТИЦИОННЫХ ПОРТФЕЛЕЙ

ДОХОДНОСТЬ И РИСК ПОРТФЕЛЯ

Дискретное вероятностное пространство состояний рынка

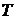Рассмотрим процесс инвестирования с точки зрения индивидуального инвестора, который располагая некоторым начальным капиталом , хочет инвестировать его на некоторый промежуток времени (инвестиционный горизонт) в доступные для него активы. Тем самым он формирует так называемый инвестиционный портфель ценных бумаг . В конце периода T инвестор реализует все активы портфеля (или оценивает рыночную стоимость активов) по некоторой стоимости . Естественно, что он желает максимизировать конечную стоимость портфеля или доходность портфеля в виде .

Этот процесс сталкивается с большими сложностями в виду неопределенности будущих цен и, следовательно, будущего дохода инвестора от реализации активов своего портфеля. Однако инвестор, обладая информацией о прошлых ценах (доходностях) ценных бумаг, может заметить, что эти изменения обладают некоторой статистической устойчивостью, что позволяет ему построить вероятностную модель рынка ценных бумаг.

Обозначим множество состояний рынка ценных бумаг как:

,

где - отдельные состояния рынка. Каждому состоянию поставим в соответствие некоторую априорную вероятность , причем . Тем самым, инвестор определяет вероятностное пространство 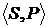, которое можно представить в виде таблицы:

			…		…
			…		…

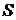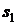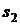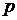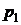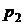Будем считать, для упрощения изложения, что m – конечное число.

Таблица 1.

Состояние рынка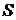	Вероятность	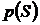Доходности активов (в %)
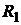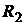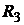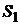	0,3			-10
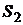	0,6
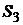	0,1		-20

Оцените доходности и риски данных активов.

Решение. Составим законы распределения случайных величин 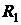, 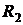и :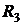

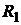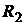							-20		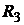	-10
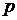	0,9	0,1		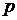	0,3	0,6	0,1		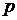	0,3	0,7

Тогда ожидаемые доходности равны:

,

,

.

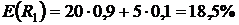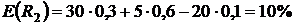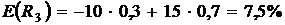Оценим риски этих активов:

, ;

, ;

, .

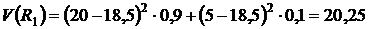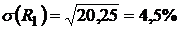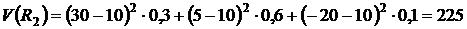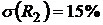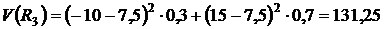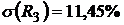Полученные результаты можно представить в виде следующей таблицы:

Таблица 2

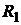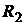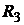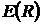	18,5		7,5
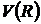	20,25		131,25
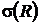	4,5		11,45

Из рассмотренного примера видно, что наибольшей доходностью 18,5% и наименьшим риском 4,5% обладает актив 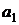, и если инвестор при принятии инвестиционных решений основывается лишь на рассмотренных выше характеристиках доходности и риска, то он должен инвестировать весь свой капитал в актив .

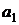Другими словами, если речь идет о выборе наилучшего актива, удовлетворяющего условиям:

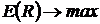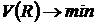, , (3)

то оптимальный портфель должен состоять только из актива .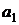

АБСОЛЮТНЫЙ И ОТНОСИТЕЛЬНЫЙ МЕТОДЫ

ОПИСАНИЯ ПОРТФЕЛЯ

Простейший способ описания портфеля состоит в указании количества активов того или иного вида, входящих в портфель. То есть, если

-

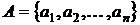полный перечень активов рынка, то портфель можно задать как вектор

, (7)

где - количество единиц актива , входящего в портфель.

Если - начальный капитал, а - начальная цена единицы актива , то необходимо выполнение условия

,

где - стоимость актива , то есть

. (8)

Описание портфеля с помощью структурного вектора (7) с условием (8) можно назвать абсолютным методом. Однако чаще применяется относительный метод описания портфеля, когда он задается вектором относительных весов каждого актива:

, (9)

где , то есть:

. (10)

Здесь условие (10) называют основным ограничением, которому удовлетворяет вектор, представляющий портфель.

Например, в № 3 портфель имел вид .

Отметим также, что любой вектор можно разложить по базисным векторам (ортам) , , … , , в виде:

.

В частности, вектор из № 3 будет выглядеть как:

.

ХАРАКТЕРИСТИКИ ПОРТФЕЛЯ

Так как портфель состоит из различных активов, то есть является своеобразным «составным» активом, то для него можно ввести все характеристики, установленные выше для активов.

Если доходности (реализованные) активов равны , то реализованная доходность всего портфеля будет равна:

.

Если же доходности активов рассматривать как случайные величины , то доходность портфеля как случайной величины, будет равна

, (11)

что позволяет получить вероятностные характеристики портфеля:

- (12)

ожидаемая доходность портфеля;

, (13)

или

- (13’)

ожидаемый риск портфеля.

Последняя формула следует из свойств дисперсии:

,

.

И если обозначить через - вектор ожидаемых доходностей активов, то

, (12’)

где - скалярное произведение векторов;

, (7”)

где

-

произведение ковариационной матрицы С, на вектор-столбец ( - вектор-строка).

Или в матричной форме:

, .

№ 5. Вычислить характеристики портфеля в условиях № 3.

Решение. Так как

, ,

,

то

,

.

То есть мы получили те же самые значения, но с использованием понятий матричной алгебры.

ВИДЫ ПОРТФЕЛЬНЫХ СТРАТЕГИЙ

Из определения относительных весов

,

можно сделать вывод, что для всех активов , или . Портфель такого вида называют стандартным, или говорят, что инвестор находится по каждому активу в длинной (long) позиции. Обычно это означает, что инвестор за счет своих средств покупает актив с целью его последующей продажи (закрытие позиций). Такая покупка совершается при ожидании повышения цены актива, что позволяет инвестору получить доход от разности цен покупки и продажи актива.

Однако, если инвестор относительно некоторого актива уверен в понижении его стоимости, то он может совершить сделку, называемую короткой продажей (short sale). Для этого он берет данный актив взаймы у другого инвестора, сразу же продает его, а потом покупает его по сниженной цене и возвращает его своему кредитору. Теоретически доходность такой операции может быть бесконечно большой, так как не требует никакого начального капитала; но зато и риск ее теоретически бесконечен, так как при повышении цены на такой актив, инвестор вынужден покупать его уже по более высокой цене.

Инвестор, осуществив короткую продажу, может на вырученные деньги купить и другие активы, что приводит к перераспределению стоимости активов (весов) портфеля. Пусть начальный капитал был равен , стоимость проданного (с короткой позиции) актива равна , тогда весь его капитал составит величину . На эту сумму он покупает активы 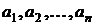, затратив при этом на актив сумму . Тогда

,

или

.

Разделив обе части этого равенства на , получим:

,

где . И если ввести обозначение , то снова будет справедливым условие (10):

.

То есть портфель инвестора снова описывается с помощью вектора с основным ограничением (10), только некоторые компоненты этого вектора могут быть отрицательными.

Следует отметить, что хотя короткие продажи вполне допустимы на большинстве фондовых бирж запада, но в виду особой рискованности таких операций, могут вводиться ограничения на общую величину коротких позиций в сделках. Другими словами на компоненты вектора могут накладываться определенные ограничения, и портфель, удовлетворяющий этим ограничениям (условиям данного рынка) называется допустимым. Такие портфели и будем рассматривать в дальнейшем.

Модель Блека

Здесь допустимыми являются любые портфели, удовлетворяющие основному ограничению (10):

.

Класс таких портфелей образует - мерную гиперплоскость n-мерного пространства :

,

где .

Например, при - это прямая , проходящая через точки и .

Рис. 1. Геометрическая иллюстрация модели Блека для двух переменных

а при - плоскость в , проходящая через единичные точки.

Модель Блека позволяет теоретически реализовать любую, сколь угодно большую доходность. Например, если портфель состоит из двух активов 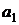и с доходностями , , то портфель имеет доходность:

,

и при .

Естественно, что это происходит за счет сильного увеличения риска.

Модель Марковица

В этой модели допустимыми являются только стандартные портфели, то есть:

, .

Класс допустимых портфелей образует стандартный - мерный симплекс в пространстве :

.

При - это отрезок прямой, соединяющей точки и ;

Рис.2. Геометрическая иллюстрация модели Марковица для двух переменных

а при - это - мерный симплекс с вершинами в единичных точках:

Рис. 3. Геометрическая иллюстрация модели Марковица для переменных

Модель Марковица характеризуется ограниченностью доходности портфеля. Так, если - наибольшая доходность активов, то

,

то есть доходность любого стандартного портфеля не превышает наибольшей доходности активов.

ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИНВЕСТИЦИОННЫХ ПОРТФЕЛЕЙ