Иммунизация портфеля облигаций

Под иммунизацией портфеля облигаций понимается такое управление портфелем, которое обеспечивает более высокий уровень его доходности в течение некоторого интервала времени при изменении рыночной процентной ставки как в меньшую, так и в большую сторону относительно первоначального значения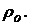

Покажем возможность такого управления портфелем на примере бескупонных облигаций. Для этого сравним доходность двух портфелей. Предположим, что первый портфель состоит из облигаций номинальной стоимостью 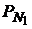со сроком до погашения 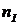лет. Рыночная стоимость данного портфеля и его дюрация будут равны:

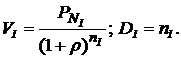(5.41)

Второй портфель сформируем из двух облигаций с номинальными стоимостями 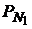и и 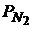сроками до погашения соответственно равным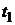и и 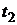лет, которые будут удовлетворять неравенству:

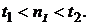
Портфель, состоящий из этих двух облигаций, будем считать облигацией II.

Текущая стоимость этого портфеля и его дюрацию можно определить по формулам:

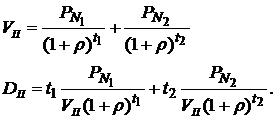(5.42)

При приобретении портфелей I и II они должны быть эквивалентны, т. е. должны иметь одинаковые рыночные стоимости и дюрации:

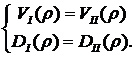(5.43)

Из решения системы уравнений (5.43) определяются характеристики облигаций, составляющие портфель II, которые обеспечивают эквивалентность портфелей при некоторой доходности 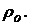На рис. 5.9 приведены зависимости текущей рыночной стоимостей портфелей I и II в зависимости от доходности 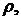рассчитанные по данным примера 5.3. Из приведенных графиков видно, что кривая II текущей стоимости второго портфеля является более выпуклой, так как выполняется неравенство:

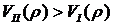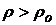при и 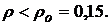(5.44)

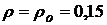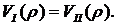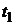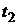При обеспечивается равенство текущих стоимостей портфелей Определим требования к срокам до погашения и облигаций портфеля II. Для этого вычислим вторые производные от текущих доходностей первого и второго портфелей:

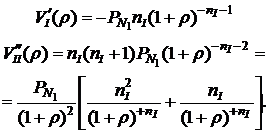(5.45)

Умножив и разделив данное выражение на 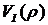, получим:

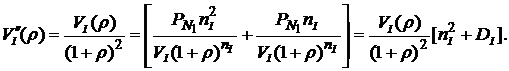
Аналогично для второго портфеля получим:

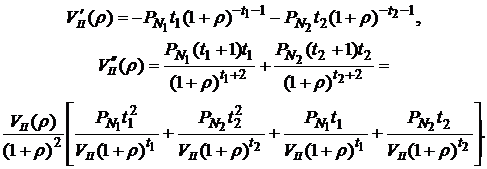(5.46)

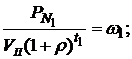
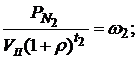
С учетом того, что отношения 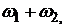определяют стоимостную долю первой и второй облигаций в портфеле II, выражение (5.46) можно записать в виде:

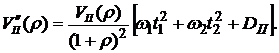(5.47)

Для выполнения неравенства (5.44) вторая производная (выпуклость) 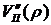должна быть больше, чем вторая производная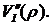

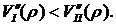(5.48)

С учетом условий (5.43) 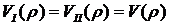и 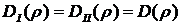и с учетом формул (5.45) и (5.47) неравенство (5.48) можно записать в виде:

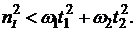(5.49)

Из условия равенства дюраций портфелей 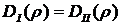можно записать:

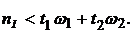(5.50)

Подставляя данное равенство в формулу (5.49), получим:

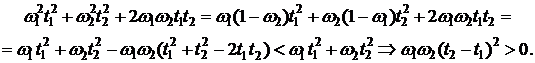
Так как данное неравенство всегда соблюдается, из этого следует вывод, что для соблюдения неравенств (5.48) и (5.49) необходимо и достаточно выполнение условия (5.50) о равенстве дюраций первого I и второго II портфеля облигаций.

Таким образом, для выполнения условия (5.43) достаточно потребовать, чтобы выполнялись условия:

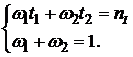(5.51)

Рассмотрим иммунизацию портфеля облигаций на примере.

Пример 5.3. Сформировать портфель из четырехгодичной 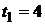и восьмигодичной 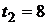бескупонных облигаций, иммунизирующий портфель, состоящий из одной бескупонной пятигодичной облигации номинальной стоимостью 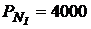руб. при доходности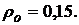

Решение: Определим номинальные и текущие стоимости облигаций портфеля II из решения системы уравнений (5.51), которая для данных условий будет иметь вид:

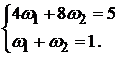
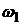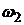Из решения данной системы уравнений находим стоимостные доли и облигаций портфеля II:

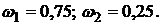
Определяем текущую стоимость облигаций портфеля I:

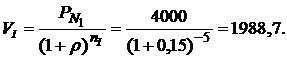
С учетом равенства 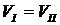и стоимостных долей облигаци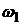й и 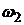определяем текущие стоимости облигаций, входящих в портфель II:

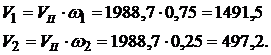
Определяем номинальные стоимости этих облигаций:

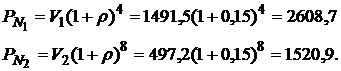
Результаты расчетов приведены также в табл. 5.4.

Таблица 5.4

r	0,03	0,07	0,11	0,15	0,19	0,23	0,27
VI	3450,4	2851,9	2373,8	1988,7	1674,2	1420,8	1210,7
VII	3518,4	2875,3	2378,4	1988,7	1679,1	1430,1	1227,5

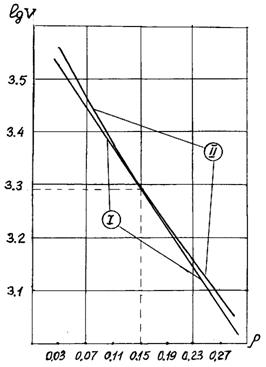
Рис. 5.9. Зависимости текущей рыночной стоимости портфелей I и II

от доходности ρ

Рассчитаем зависимость текущей стоимость первого и второго портфеля облигаций от времени, прошедшего после их приобретения. Расчет данных зависимостей проводится по формулам:

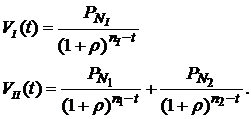
Результаты расчетов приведены в табл. 5.5 и на рис. 5.10.

Таблица 5.5

	t		0,5		1,5		2,5		3,5
r = 0,07	VI	2851,9	2950,1	3051,6	3156,6	3265,2	3377,5	3493,7	3614,0	3738,3
VII	2875,3	2974,3	3076,6	3182,5	3292,0	3405,2	3522,4	3643,6	3769,0
∆V	23,4	24,2	25,0	25,9	26,8	27,7	28,7	29,6	30,7
r = 0,3	VI	1077,3	1228,3	1400,5	1596,8	1820,7	2075,9	2366,9	2698,6	3076,9
VII	1099,8	1254,0	1429,8	1630,2	1858,7	2119,3	2416,3	2755,0	3141,2
∆V	22,5	25,7	29,3	33,4	38,0	43,4	49,4	56,4	64,3

На рис. 5.10 приведена зависимость разности текущих стоимостей второго и первого портфеля облигаций (∆V = V_II(t) - V_I(t). Из расчетов видно, что при уменьшении и увеличении значений доходности облигаций к погашению второй портфель облигаций имеет бóльшую текущую стоимость, чем первый. При увеличении времени разница в текущих стоимостях облигаций портфеля II и I увеличивается.

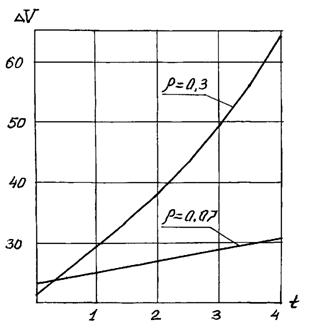
Рис. 5.10. Зависимость разности текущих стоимостей второго