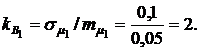Портфель из двух видов ценных бумаг

Эффективность и риск портфеля из двух видов ценных бумаг можно оценить по формулам:

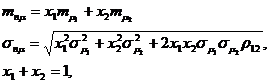(4.11)

где 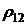- коэффициент корреляции доходностей по ценным бумагам первого и второго вида;

х₁ и х₂ – ценовая доля первого и второго вида ценных бумаг.

Коэффициент вариации портфеля, состоящего из двух видов ценных бумаг, можно определить по формуле:

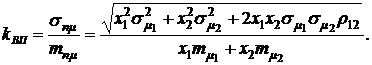(4.12)

На рис. 4.1а приведены зависимости эффективности портфеля ценных бумаг 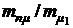и рисков портфеля ценных бумаг 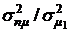от ценовой доли бумаг первого вида х₁ при 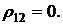Зависимость 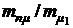от х₁ приведена на рис. 4.1а пунктирной линией при трех значениях отношения эффективностей ценных бумаг второго и первого вида:

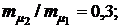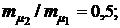1. 2. 3.

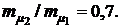
Эта зависимость имеет линейный характер. Эффективность портфеля ценных бумаг изменяется от 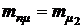при х₁=0 до 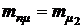при х₁=1. Зависимость отношения 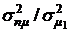, характеризующего риски портфеля ценных бумаг, от х₁ приведена на рис. 4.1а сплошными линиями при трех значениях отношения:

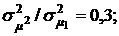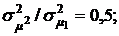1. 2. 3.

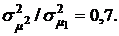
Из приведенных графиков видно, что риск портфеля ценных бумаг двух видов 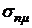при определенном оптимальном значении ценовой доли бумаг х₁ может иметь минимальное значение. Так например, при 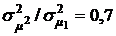минимальное значение 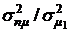при х₁=0,4 будет равно 0,412. При оптимальном значении х₁ выполняется соотношение 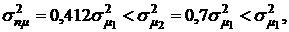т. е. при оптимальном распределении ценовой доли бумаг риск портфеля ценных бумаг двух видов будет меньше, чем риски ценных бумаг первого и второго видов (см. п. 3.3.1).

На рис. 4.1б приведены зависимости коэффициента вариации портфеля ценных бумаг 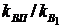от ценовой доли бумаг первого вида х₁ при 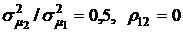и при трех значениях отношения:

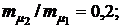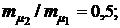1. 2. 3.

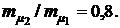
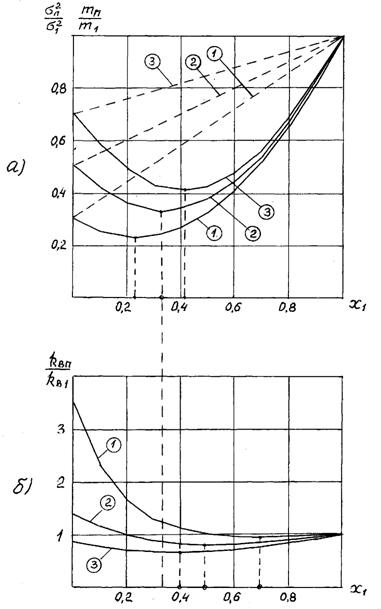
Рис. 4.1. Зависимость риска независимых бумаг двух видов от ценовой доли бумаг первого вида

Из приведенных графиков видно, что при определенных оптимальных значениях х₁ имеют место минимальные значения коэффициента вариации портфеля ценных бумаг. При 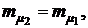когда эффективности ценных бумаг первого и второго вида одинаковы, минимальное значение коэффициента вариации портфеля 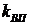ценных бумаг будет при ценовых долях бумаг первого х₁ и второго х₂ вида, определяющихся формулами (3.21), а минимальное значение 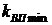определится формулой (3.22).

Оптимальные значения распределения ценовых долей бумаг х₁ и х₂, обеспечивающие минимальное значение риска портфеля 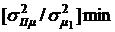(рис. 4.1а), также могут быть определены по формулам (3.21).

При 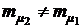оптимальные значения распределения ценовых долей бумаг первого х₁ и второго вида х₂ могут быть найдены дифференцированием формул (4.11) и (4.12) по х₁ и приравниванием производной нулю.

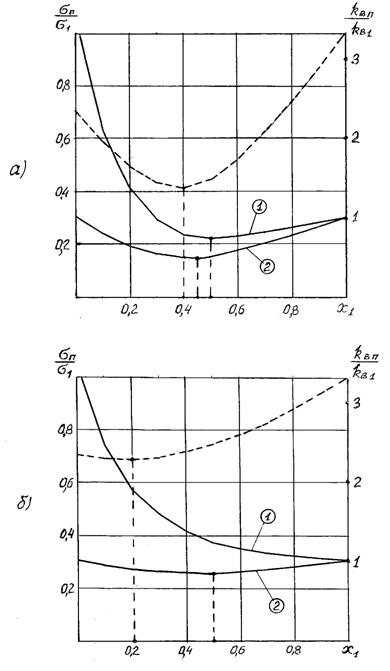
Рис. 4.2. Зависимость риска зависимых ценных бумаг двух видов от ценовой доли бумаг первого вида

Оптимальное распределение ценовых долей бумаг х₁ и х₂, обеспечивающих минимум среднеквадратического значения рисков 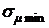портфеля зависимых ценных бумаг, можно определить по формулам:

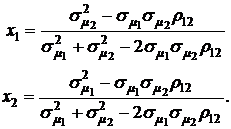(4.13)

Графики зависимости отношения 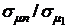от ценовой доли бумаг первого вида х₁ при 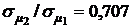приведены пунктирными линиями для 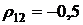на рис. 4.2а и для 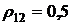на рис. 4.2б. Из рисунков видно, что при отрицательных значениях коэффициента корреляции ценных бумаг имеет место оптимальное распределение ценовых долей бумаг х₁ и х₂ (формула (4.13). При положительных значениях коэффициента корреляции ценных бумаг 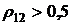минимума значения 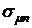не наблюдается.

Сплошными линиями на рис. 4.2а и б приведены зависимости отношения 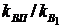от ценовой доли бумаг первого вида х₁ 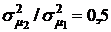при и при 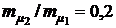(кривая 1) и 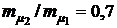(кривая 2). Из приведенных графиков видно, что оптимальные значения х₁ и х₂, обеспечивающие минимумы 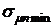и 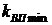не совпадают.

Оптимальное распределение ценовой доли бумаг первого и второго вида, обеспечивающее минимум коэффициента вариации портфеля ценных бумаг 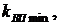может быть рассчитано по формулам:

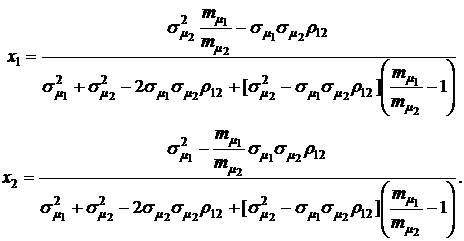(4.14)

4.4. Портфель из m-независимых ценных бумаг

Для независимых ценных бумаг парные коэффициенты корреляции доходностей этих ценных бумаг равны нулю:

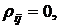при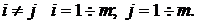

В этом случае риск портфеля этих ценных бумаг определяется формулой:

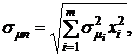
где 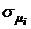- риски доходностей ценных бумаг i-го вида, определяющиеся среднеквадратическим значением доходностей; х_i – ценовая доля бумаг i-го вида.

Определим структуру портфеля ценных бумаг минимального риска 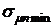. Эта же структура портфеля ценных бумаг обеспечивает минимум 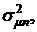поэтому оптимальное распределение ценовых долей ценных бумаг будем искать из условия:

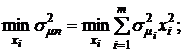при 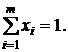(4.15)

Данная задача нахождения оптимального распределения 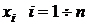может быть решена с помощью функции Лагранжа. Для задачи, формализуемой условиями (4.15), функция Лагранжа имеет вид:

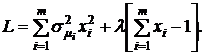
Для нахождения оптимальных значений 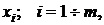обеспечивающих минимум 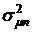, составим систему уравнений из производных функции Лагранжа по 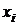и λ.

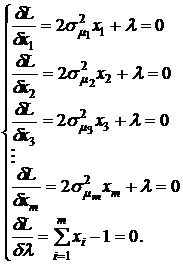(4.16)

Для получения конкретных результатов далее ограничимся портфелем, состоящим из четырех видов бумаг m = 4. В этом случае система уравнений (4.16) будет включать пять уравнений, четвертое из которых будет иметь вид:

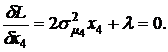
Последовательно вычитая из первого уравнения второе, затем третье и затем четвертое, получим:

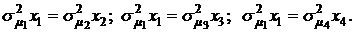
Определим из этих уравнений значения х₂; х₃ и х₄

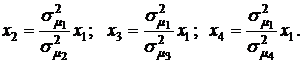(4.17)

Подставим эти значения в пятое уравнение системы (4.16), получим:

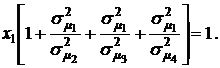
Отсюда для х₁ получим:

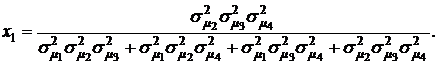(4.18)

С учетом формул (4.17) для ценовых долей бумаг второго, третьего и четвертого видов получим:

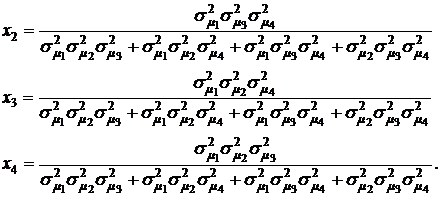(4.19)

Минимальное значение риска портфеля из четырех видов ценных бумаг определится формулой:

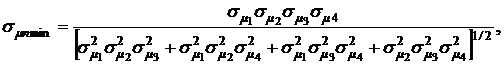(4.20)

а средняя доходность такого портфеля будет равна:

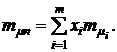
Пример 4.1. Для портфеля из четырех видов ценных бумаг со средней доходностью 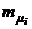и рисками 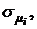соответственно равными:

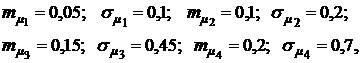
найти оптимальную структуру портфеля минимального риска, его риск 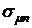и среднюю доходность .

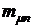Решение: По формулам (4.19) находим оптимальные значения ценовых долей бумаг каждого вида.

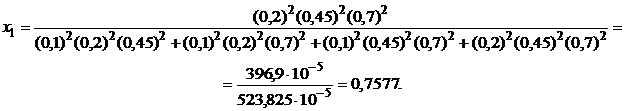
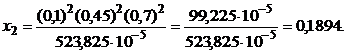
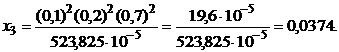
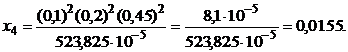
По формуле (4.20) определяем минимальное значение риска портфеля ценных бумаг:

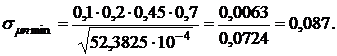
Для средней доходности такого портфеля получим:

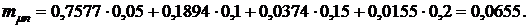
Из приведенных расчетов видно, что риск портфеля оказался меньше, чем риск наименее рискованных бумаг первого вида 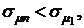а средняя доходность (эффективность) портфеля ценных бумаг оказывается больше, чем доходность бумаг первого вида 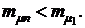Таким образом, для оптимального портфеля минимального риска коэффициент вариации портфеля ценных бумаг равен 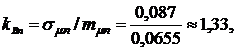и это значение меньше, чем коэффициент вариации наименее рискованных бумаг первого вида