Сравнение финансовых потоков и рент

При принятии финансовых решений часто возникает необходимость выбора между финансовыми потоками с различными параметрами. Для обоснованного принятия решений необходимо уметь сравнивать финансовые потоки и ренты. При сравнении финансовых потоков и рент какие-то их параметры должны быть одинаковыми, какие-то параметры должны быть сопоставимыми, а какие-то могут отличаться. Сравнение финансовых потоков и рент должно осуществляться по конечной наращенной или современной их стоимости, при этом рассматриваются финансовые потоки с равными сроками. На рис. 2.9 приведены зависимости современной А и наращенной конечной S стоимостей годовой ренты от годовой процентной ставки при сроке ренты 2 и 5 лет. Из рисунка видно, что с увеличением годовой процентной ставки современная стоимость ренты А уменьшается, а наращенная, конечная стоимость ренты увеличивается.

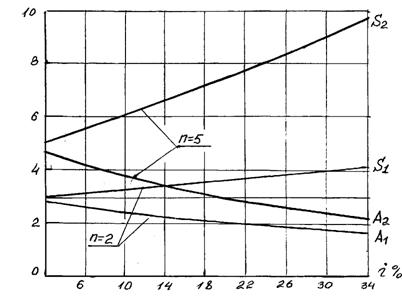
Рис. 2.9. Зависимость современной и наращенной стоимостей годовой ренты

Рассмотрим два потока

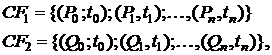
отличающиеся лишь размерами платежей 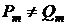. Вполне очевидно, что при выполнении условия

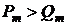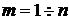при (2.68)

современная дисконтированная и конечная наращенная стоимость при любых значениях процентной ставки "i" будет больше для первого потока. Аналогично первый финансовый поток будет предпочтительным для любых значений процентной ставки дисконтирования при выполнении условия

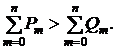(2.69)

Но при выполнении условий (2.68) и (2.69) первый и второй финансовые потоки не являются сопоставимыми (эквивалентными), а значит, их сравнение по стоимости является некорректным. Введем условие сопоставимости финансовых потоков в виде

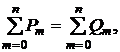(2.70)

т. е. сопоставимыми будем считать финансовые потоки, у которых сроки ренты и сумма всех платежей одинаковы. Сравним между собой годовую и r-срочную ренту. Для этих двух рент условие сопоставимости (2.70) выполняется, когда размер платежей r-срочной ренты в r раз меньше платежей годовой ренты 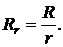Тогда для отношения современной (или наращенной) стоимости r-срочной ренты к современной (или наращенной) стоимости годовой ренты в соответствии с формулами (2.6), (2.8) и (2.21), (2.23) получим

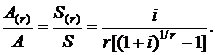(2.71)

Из формулы (2.71) видно, что отношение 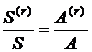не зависит от срока ренты "n".

На рис. 2.10 приведены графики зависимости отношений 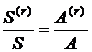от количества платежей в году r при двух значениях годовой процентной ставки. Из них видно, что r-срочная рента является более предпочтительной по сравнению с годовой рентой.

Сравним между собой обычную годовую и арифметическую ренты. Вычислим размеры платежей арифметической ренты, при которых выполняется условие сопоставимости рент (2.70). При сроке рент, равном "n" лет, суммарные платежи для обычной годовой ренты будут равны nR.

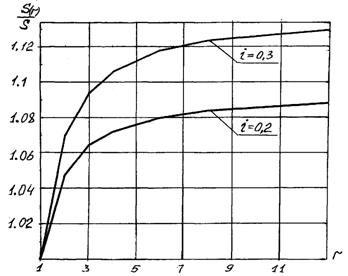
Рис. 2.10. Зависимость отношений 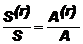от количества платежей в году

Для арифметической ренты суммарные платежи будут равны

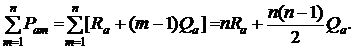(2.72)

Тогда условие сопоставимости обычной годовой и арифметической рент можно записать в виде

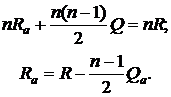(2.73)

Подставив формулу (2.73) в (2.56) с учетом формул (2.7) и (2.8), для отношения наращенных стоимостей арифметической к годовой ренте получим

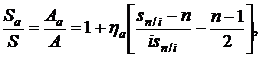(2.74)

где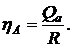

Графики зависимости отношения S_a/S от значений процентной ставки "i" при различных значениях срока ренты "n" и относительной разности 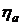арифметической прогрессии приведены на рис. 2.11. Из приведенных графиков видно, что при убывающей арифметической прогрессии 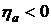предпочтительной является арифметическая рента. При возрастающей арифметической прогрессии платежей 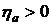предпочтительной оказывается обычная годовая рента, причем скорость возрастания при 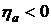(убывания при 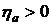) отношения S_a/S увеличивается при увеличении срока ренты "n" и относительной разности 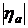арифметической прогрессии платежей.

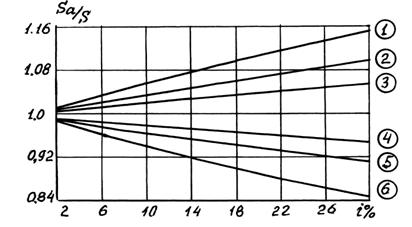
Рис. 2.11. Зависимость отношений 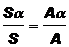от годовой процентной ставки(1 – n = 5, 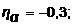2 – n = 3, 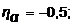3 – n = 3, 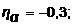4 – n = 3,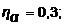

5 – n = 3, 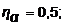6 – n = 5,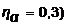

Приведем сравнение геометрической ренты с обычной годовой рентой. Вычислим размеры платежей геометрической ренты, при которых выполняется условие сопоставимости (2.70) сравниваемых рент

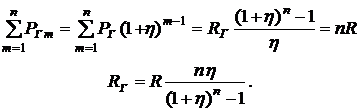(2.75)

Подставив формулу (2.75) в (2.64) с учетом формул (2.7) и (2.8), для отношения конечных наращенных сумм геометрической и простой годовой рент получим

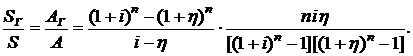(2.76)

При 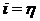данная формула может быть преобразована к виду

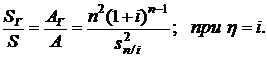(2.77)

На рис. 2.12 приведены графики зависимости отношения 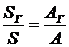от годовой процентной ставки "i" при различных значениях срока ренты "n" и величины " 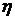", характеризующей темпы роста платежей. Из приведенных графиков видно, что при убывании размеров платежей 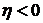предпочтительной оказывается геометрическая рента по сравнению с годовой рентой. При 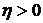предпочтение следует отдать обычной годовой ренте. Скорость изменения отношения 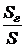увеличивается при увеличении срока ренты "n" и темпов изменения размеров платежей " ".

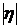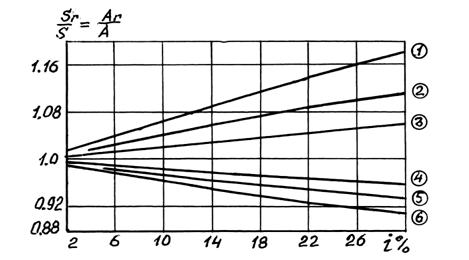
Рис. 2.12. Зависимость отношений 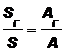от годовой процентной ставки(1 – n = 5, 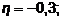2 – n = 3, 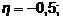3 – n = 3, 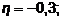4 – n = 3,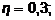

5 – n = 3, 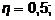6 – n = 5,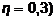

Оценим, насколько предпочтительной является рента с m-кратным начислением процентов по сравнению с обычной годовой рентой. Для этого вычислим отношения 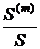и 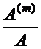, используя формулы (2.46) и (2.48), а также формулы (2.6) и (2.8):

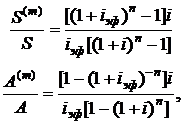(2.78)

где 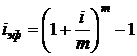- эффективное значение годовой процентной ставки при m-кратном начислении процентов.

Результаты расчетов отношени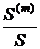й и 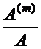от кратности начисления процентов m по формулам (2.78) приведены на рис. 2.13 для двух значений годовой процентной ставки 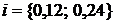и срока ренты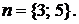

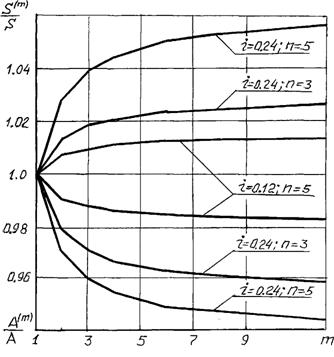
Рис. 2.13. Зависимости отношени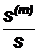й и 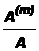от кратности начисления процентов "m"

Из приведенных графиков видно, что при увеличении кратности начисления процентов увеличивается отношение 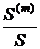и уменьшается отношение 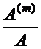. Из этого следует, что рента с m-кратным начислением процентов является более предпочтительной по сравнению с обычной годовой рентой. При увеличении годовой процентной ставки "i" и срока ренты "n" отношение 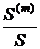увеличивается. Так например, при i = 0,24 и сроке ренты n = 5 лет конечная наращенная сумма 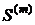ренты с ежемесячным начислением процентов m = 12 примерно на 5,6 % превышает конечную наращенную сумму обычной годовой ренты.

Проведем сравнение r-срочной ренты при m-кратном начислении процентов с обычной годовой рентой. Современная 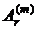и финальная наращенная 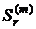стоимости r-срочной ренты при m-кратном начислении процентов определяются формулами (2.50) при 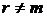и формулами (2.51) при 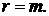Для сравнения рент поделим значения стоимосте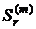й и 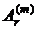r-срочной ренты при m-кратном начислении процентов на соответствующие значения стоимостей простой годовой ренты и получим

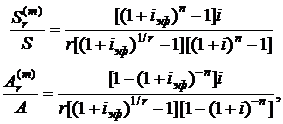(2.79)

где 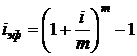эффективное значение годовой процентной ставки при m-кратном начислении процентов.

Формулы (2.79) применяются для случая 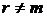. При 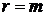формулы (2.79) упрощаются и могут быть записаны в виде

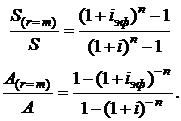(2.80)

Графики зависимости отношени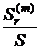й и 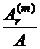от кратности начисления процентов "m" приведены на рис. 2.14.

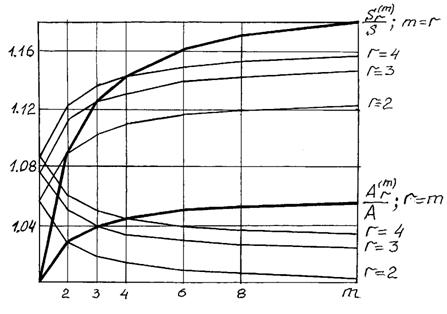
Рис. 2.14. Зависимости отношени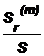й и 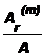от кратности начисления процентов "m"

Расчет проводился для годовой процентной ставки i = 0,24 и срока ренты n = 5 лет.

При равенстве значений 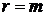отношения 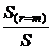и 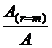увеличиваются с ростом кратности начисления процентов "m". При 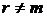отношение 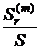увеличивается, а отношение 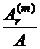уменьшается с ростом кратности начисления процентов.

При 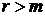справедливы неравенства 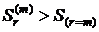и 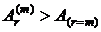, а при 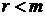наоборот 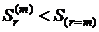и и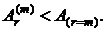з приведенных расчетов следует, что наиболее предпочтительная является r-срочная рента с m-кратным начислением процентов при 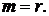Так например, при годовой процентной ставке i = 0,24 и сроке ренты n = 5 лет, рента с ежемесячными платежами r = 12 и ежемесячным начислением процентов m = 12 дает выигрыш по конечной наращенной сумме примерно на 18 % по сравнению с обычной годовой рентой.

Конверсия рент

При меняющихся экономической ситуации, финансовом состоянии субъектов экономической деятельности, особенно в условиях кризиса, часто возникает необходимость изменения условий выплаты ренты, т. е. замены одной ренты на другую или разового платежа, либо, наоборот, разовый платеж заменить рентой (рассрочка платежа), а также заменить несколько рент одной. Все вышеперечисленные операции называют конверсией рент. При конверсии рент должно выполняться одно общее правило – в момент заключения сделки о конверсии рент t_k современные стоимости старых рент, приведенных к моменту времени t_k, и современные стоимости новых рент должны быть равны. Это правило следует из естественного требования, чтобы конверсия рент не меняла финансового положения сторон сделки, т. е. на момент заключения сделки о конверсии рент должен соблюдаться принцип их финансовой эквивалентности.

Данный принцип определяет следующий алгоритм расчета параметров новой ренты.

1. Определяется современная стоимость старой (старых) ренты, приведенная к моменту заключения сделки t_k о конверсии рент.

2. В случае объединения нескольких рент современные их стоимости, приведенные к моменту времени t_k, складываются и дают современную стоимость новой ренты.

3. Зная современную стоимость новой ренты, рассчитывают параметры новой ренты.

Рассмотрим такие примеры конверсии рент как рассрочка платежа; выкуп ренты; замена одной ренты новой рентой; замена нескольких рент с разными параметрами одной новой рентой.

1) Рассрочка платежа. Предположим, что некоторый субъект экономической деятельности (должник) имеет задолженность в сумме 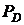рублей перед кредитором, которая должна быть погашена в установленное время t₀. При невозможности погасить задолженность в установленное время за счет собственных средств должник может обратиться в банк с просьбой о предоставлении ему кредита в сумме 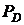или договориться с кредитором о погашении задолженности не единовременным платежом, а рентными платежами. При этом все условия предоставления и погашения банковского кредита или рентных платежей кредитору определяются из условия равенства долга современной стоимости ренты.

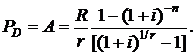
При погашении задолженности за счет банковского кредита все параметры ренты по погашению кредита определяются методикой банка. При согласии кредитора заменить единовременное погашение задолженности рентными платежами все параметры ренты (R, r, i, n) определяются договоренностью должника и кредитора.

2) Выкуп ренты. Выкупом ренты называется замена ренты единовременным платежом. Данную операцию рассмотрим на примере погашения кредита аннуитетом. Предположим, что кредит на сумму "D" руб. выдан на "n" лет под "i" процентов годовых, и его погашение осуществляется постоянными ежеквартальными платежами. График платежей в погашение кредита представляет собой r-срочную ренту постнумерандо (r = 4) с количеством платежей, равным "r · n". Размер аннуитета для данной ренты определяется формулой (2.33):

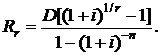
Ссудозаемщик регулярно осуществлял выплаты по кредиту в течение "k" платежей (рис. 2.15).

Рис. 2.15. Финансовый поток выплат по кредиту

При наступлении k-го платежа вместе с очередным платежом у ссудозаемщика появилась возможность досрочного погашения всей оставшейся задолженности по кредиту. Приведенную стоимость данной ренты 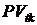к моменту k-го платежа по аналогии с формулой (2.1) можно записать в виде

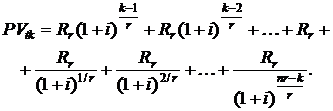(2.81)

Первые k слагаемых в формуле (2.81) определяют конечную стоимость выплаченной части ренты

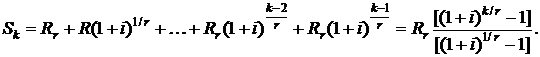(2.82)

Остальные nr – k слагаемых в формуле (2.81) определяют стоимость невыплаченной части ренты, приведенной к моменту времени k-го платежа

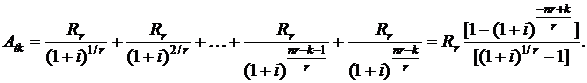
Эта стоимость определяет оставшуюся невыплаченную при k-м платеже сумму кредита D_k.

Для полного погашения кредита вместе с k-м платежом должна быть внесена сумма

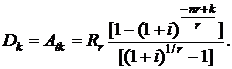(2.83)

Рассчитываем сумму, необходимую для досрочного погашения кредита при k = 2 втором платеже для примера, рассматриваемого в п. 2.4. В этом примере рассматриваются следующие исходные данные: D = 100 тыс. руб., n = 1 год, r = 4, i = 20 %. Размер разового квартального платежа составляет 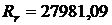руб.

В соответствии с формулой (2.83) необходимая сумма для полного погашения кредита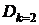

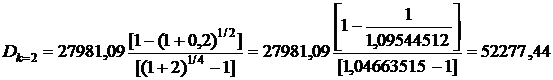руб.

Данная сумма совпадает с текущей оставшейся задолженностью по кредиту, приведенной в табл. 2.1 п. 2.4 при втором (k = 2) платеже.

3) Замена двух рент одной новой рентой. Рассмотрим две ренты, график платежей по которым приведен на рис. 2.16.

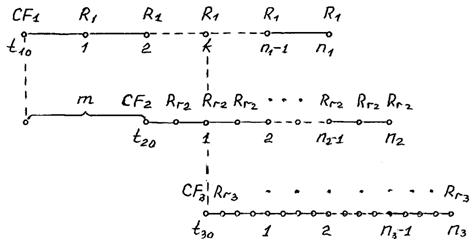
Рис. 2.16. Финансовые потоки при замене двух рент одной новой рентой

Первая рента является годовой рентой с ежегодными платежами R₁, годовой процентной ставкой i₁ и сроком ренты n₁ лет. Вторая рента является r-срочной рентой с платежами размером 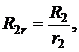годовой процентной ставкой i₂ и сроком ренты n₂ лет (n₂r₂ платежей).

Дата начала второй ренты t₂₀ от даты начала первой ренты t₁₀ сдвинута на "m" лет, т. е. 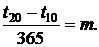Плательщик рент принял решение с даты t_k объединить оставшиеся выплаты по первой и второй рентам и заменить их третьей рентой. Будем считать, что дата конверсии рент t_k удовлетворяет условию 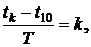т. е. по первой ренте до даты t_k совершено k платежей и осталось совершить n₁ – k платежей. Приведенную стоимость первой ренты к дате t_k по аналогии с формулой (2.1) можно записать в виде

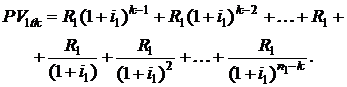
Приведенная к дате t_k стоимость невыплаченной части первой ренты является суммой (n₁ – k) членов убывающей геометрической прогрессии с первым членом 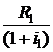, знаменателем 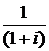и определится формулой

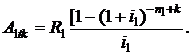
Из рис. 2.16 видно, что по второй ренте до даты t_k совершено платежей. Приведенную стоимость второй ренты к дате t_k по аналогии с формулой (2.81) можно записать в виде

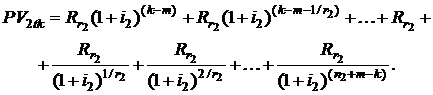
Из данной формулы видно, что приведенная к дате t_k стоимость невыплаченной части второй ренты является суммой ( 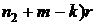членов убывающей геометрической прогрессии с первым членом 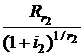, знаменателем 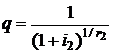и определится формулой

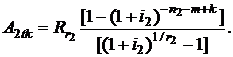
При замене нескольких рент одной новой рентой должно обеспечиваться равенство суммы приведенных к дате t_k стоимостей старых рент современной стоимости новой ренты:

.

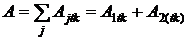Параметры новой ренты определяются из условия:

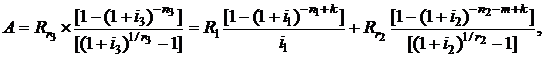(2.84)

где 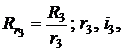и n₃ – параметры новой ренты. Срок новой ренты n₃ отсчитывается от даты t_k в годах. При расчете параметров новой ренты все параметры, кроме одного, должны быть определены по договоренности сторон, заключающих сделку о конверсии рент, а неизвестный параметр, например, 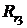, определяется из уравнения (2.84).

Контрольные вопросы и задания

1. Привести формулу для определения современной приведенной стоимости PV и финальной наращенной стоимости FV финансового потока сроком на t дней, при годовой процентной ставке i %.

2. Пояснить отличие рент постнумерандо и пренумерандо.

3. Определить современную (начальную) стоимость годовой ренты постнумерандо с размером платежей R = 40 тыс. руб. при годовой процентной ставке i = 10 % и сроке ренты n = 3 года.

4. Определить финальную (наращенную) стоимость годовой ренты пренумерандо с размером платежей 20 тыс. руб. при годовой процентной ставке i = 11 % и сроке ренты n = 4 года.

5. Финальная (наращенная) стоимость ренты постнумерандо при годовой процентной ставке i = 10 % годовых и сроке ренты 4 года составила 146410 руб. Определить начальную приведенную стоимость этой ренты.

6. Начальная стоимость годовой ренты пренумерандо при годовой процентной ставке i = 12 % и сроке ренты n = 3 года составляет 500000 руб. Определить финальную (наращенную) стоимость этой ренты.

7. Записать формулы, устанавливающие взаимосвязь между финальными и начальными стоимостями рент постнумерандо и пренумерандо.

8. Определить начальную и финальную стоимости r-срочной ренты постнумерандо при r = 4, годовой процентной ставке i = 12 %, размере годового платежа 80000 руб. и сроке ренты n = 2 года.

9. Финальная стоимость r-срочной ренты постнумерандо при r = 4 и и i = 12,56 % составила 100000 руб. Определить финальную стоимость r-срочной ренты пренумерандо.

10. Современная (начальная) стоимость ренты пренумерандо при r = 2 и и i = 10,7 % составляет 210000 руб. Определить современную (начальную) стоимость ренты постнумерандо.

11. Найти средний срок финансового потока:

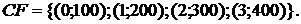
12. Начальная стоимость r-срочной ренты постнумерандо A_r, заключенной на 2 года при годовой процентной ставке i = 9 %, при ежеквартальных платежах r = 4, равна 400 тыс. руб. Определить размер ежеквартальных платежей R/r.

13. В коммерческом банке взят потребительский кредит на сумму 300 тыс. руб. сроком на 1 год под 19 % годовых. Погашение кредита осуществляется ежеквартальными платежами r = 4. Рассчитать график платежей в погашение кредита.

14. В банке взят валютный кредит в сумме D_? = 8000 евро сроком на один год под j_? = 6 % c ежеквартальными платежами. Кредит гасится из рублевых доходов ссудозаемщика. Определить суммарные рублевые выплаты по кредиту, если на момент заключения кредитного договора обменный курс валюты был равен K_?Ro = 80 и далее за каждый последующий квартал уменьшался на 2,5 рубля за 1 евро.

15. Организацией для осуществления внешнеэкономической деятельности взят рублевый кредит в сумме 1200 тыс. руб., что на момент заключения кредита соответствовало 20000 $ США (K_$Ro = 60). Кредит взят сроком на 1 год с ежеквартальными платежами под годовую процентную ставку i = 20 %. Погашение рублевого кредита осуществляется из валютных доходов организации. Определить размеры ежеквартальных рублевых платежей по кредиту, их валютные эквиваленты и суммарные валютные расходы по погашению рублевого кредита, если обменный курс валюты увеличивался за каждый последующий квартал на 1,5 рубля за 1 доллар США.

16. Определить первоначальную стоимость r-срочной ренты (r = 2), заключенной на 2 года при m-кратном начислении процентов m = 4 с размером годового платежа R = 80000 руб.

17. Определить начальную А_а и финальную стоимость S_a арифметической ренты постнумерандо, заключенной на 3 года с размером годового платежа R = R_o + (k – 1)Q, где R_o = 50 тыс. руб., Q = 10 тыс. руб., k – номер платежа. При расчетах годовую процентную ставку принять равной i = 11 %.

18. Определить финальную стоимость r-срочной геометрической ренты постнумерандо (r = 4), заключенной на n = 3 года с размером разовых ежеквартальных платежей 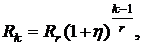где 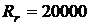руб., η = 5 %; k = 1÷(nr - 1) – номер платежа. При расчетах годовую процентную ставку принять равной i = 10 %.

19. Кредит, заключенный на n = 2 года с годовой процентной ставкой i = 18 %, погашается ежеквартальными платежами размером R = 74954,4 руб. При осуществлении пятого (k = 5) платежа ссудозаемщик планирует досрочно погасить всю оставшуюся задолженность по кредиту. Определить сумму денежных средств, которые ссудозаемщик должен внести для досрочного погашения оставшейся задолженности по кредиту.

20. Ссудозаемщик производит рентные платежи в погашение двух кредитов. Первый кредит заключен под годовую процентную ставку i₁ = 16 % на 5 лет, погашается ежегодными платежами (r₁ = 1) в размере R₁ = 157704,4 руб. Второй кредит заключен под годовую процентную ставку i₂ = 18 % на 2 года, погашается ежегодными платежами (r₂ = 4) в размере R₂ = 44972,64 руб.

При оплате третьего платежа по первому кредиту ссудозаемщик планирует заменить эти две ренты одной новой рентой с годовой процентной ставкой i₃ = 17 % с ежеквартальными платежами сроком на n₃ = 4. Определить размер платежей по новой ренте R₃, если на момент замены рент по второму кредиту осталось совершить шесть платежей.