Учет налогов при совершении финансовых операций

Рассмотрим методику учета налогов при определении эффективной процентной ставки по банковским вкладам на депозит и при получении банковских кредитов.

1) Учет налогов по депозитным договорам

Проценты по вкладам в коммерческом банке не облагаются налогами, если они не превышают ставку рефинансирования Центрального банка России, увеличенную на 5 %. Обозначим это пороговое значение 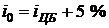. В противном случае при 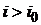с суммы доходов по процентам, превышающим ставку 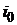, взимается налог .

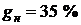Рассчитаем эффективную процентную ставку для данного случая. Наращенную величину вклада по истечении года можно определить по формуле:

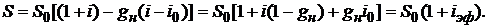
Отсюда для эффективной процентной ставки при наличии налоговых отчислений 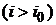получим:

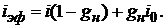(1.32)

Пример. Вклад помещен в банк под 17 % годовых 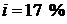. Найти эффективную процентную ставку по вкладу при ставке рефинансирования Банка России .

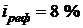Решение. Определяем ставку отсечения

.

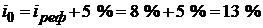По формуле (1.32) вычисляем эффективную процентную ставку при ставке налога .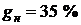

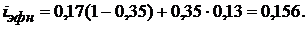
Таким образом, реальная эффективная процентная ставка с учетом уплаченных налогов будет равна 15,6 %, т. е. на 1,4 % ниже объявленной банком процентной ставки по вкладу.

2) Учет налогов по кредитным договорам

Проценты за кредит исключаются из налогооблагаемой базы налога на прибыль организации, если они не превышают ставку отсечения 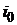по рублевым кредитам, 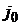- по валютным кредитам.

Для рублевых кредитов 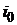превышает ставку рефинансирования 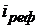Банка России на несколько процентных пунктов.

Определим эффективную процентную ставку по кредиту, если процентная ставка, указанная в кредитном договоре i, не превышает ставку отсечения 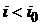. В этом случае платежи в счет погашения кредита, выплачиваемые из чистой прибыли (после уплаты налога на прибыль), можно определить по формуле:

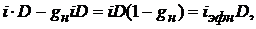
где D – сумма кредита.

Отсюда для эффективной процентной ставки получим:

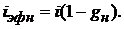(1.33)

Величину 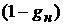называют налоговым щитом. Она показывает финансовую выгоду компании при использовании заемного капитала.

Если процентная ставка по кредиту i, указанная в кредитном договоре, превышает ставку отсечения 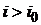, то из платы процентов за кредит iD вычитается только величина 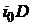. С учетом этого для эффективной процентной ставки получим:

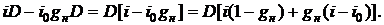
Приравнивая данное выражение значению 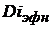для эффективной процентной ставки по кредиту, получим:

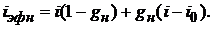(1.34)

При 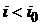разность 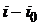в формуле (1.34) должна быть взята равной нулю и формула (1.34) совпадает с формулой (1.33).

Пример. Кредит взят под 20 % годовых. Найти эффективную кредитную процентную ставку, если ставка отсечения равна 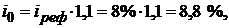а ставка налога на прибыль равна .

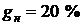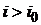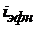Решение. Так как , то рассчитываем по формуле (1.34):

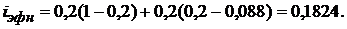
Таким образом, реально выплаченная эффективная процентная ставка по кредиту равна 18,24 %, т. е. на 1,76 % меньше процентной ставки, указанной в кредитном договоре.

Операции с валютой

Возможность конвертации рублей в валюту и обратно валюты в рубли, а также возможность получения доходов от размещения на депозитах как рублевых, так и валютных вкладов увеличивают число возможных схем проведения данных финансовых операций.

Предположим, что в наличии имеются временно свободные средства в российских рублях R, в долларах США $ и в евро ?. Сравним доходы от размещения на депозите имеющихся денежных средств.

Возможны следующие схемы получения дохода:

· Без конвертации валюты

1) R → R

2) $ → $

3) ? → ?

· С конвертацией валюты

4) R → $ → $ → R

5) R → ? → ? → R

6) $ → R → R →$

7) ? → R → R → ?

8) $ → ? → ? → $

9) ? → $ → $ →?

Для сравнения доходности всех указанных схем финансовых операций введем следующие обозначения:

P_R – сумма депозитного вклада в рублях;

P_$ – сумма депозитного вклада в долларах США;

P_? – сумма депозитного вклада в евро;

S_R; S_$; S_? - наращенная за срок депозита сумма в рублях, долларах США и евро соответственно;

K_$R0; K_$R1 – обменный курс долларов США в рубли в начале и в конце финансовой операции соответственно;

K_?R0; K_?R1 – обменный курс евро в рубли в начале и в конце финансовой операции соответственно;

K_$?0; K_$?1 – обменный курс долларов США в евро в начале и в конце финансовой операции соответственно;

n – срок депозита;

i – годовая процентная ставка по депозиту в рублях;

j_$ - годовая процентная ставка по депозиту в долларах США;

j_? - годовая процентная ставка по депозиту в евро.

Получим формулы для оценки доходности финансовых операций для всех схем с конвертацией валюты.

Для финансовых операций без конвертации валюты по схемам 1-3 формулы для определения наращенных сумм и множителей наращения приведены в п. 1.2 и 1.3.

При наличии временно свободных средств во всех трех валютах P_R; P_$ и P_? как средство снижения рисков потерь при изменении обменного курса валют рекомендуется их размещение на мультивалютном вкладе.

Рассмотрим эту финансовую операцию на конкретном примере.

Пример. В банке открыт мультивалютный вклад: 100 тыс. руб. под 13 % годовых; 5 тыс. долл. США под 5 % годовых и 10 тыс. евро под 4 % годовых. Найти эффективную процентную ставку мультивалютного вклада, если курсы обмена валют в начале и в конце годового срока депозита равны 30 и 52; 40 и 62 руб. соответственно.

Решение. Через год наращенные суммы будут равны:

S_R = P_R(1 + i) = 100 тыс. руб. (1 + 0,13) = 113 тыс. руб.

S_$= P_$(1 + j_$) = 5000 (1 + 0,05) = 5250 $.

S_?= P_?(1 + j_?) = 10000 (1 + 0,04) = 10400 ?.

Конвертируя первоначальные и наращенные суммы по курсам обмена валют на начало и окончание срока депозита, получим:

S_R0= 100000 + 5000 х 30 + 10000 х 40 = 650 тыс. руб.

S_R1= 113000 + 5250 х 52 + 10400 х 62 = 1030,8 тыс. руб.

Эффективная процентная ставка по мультивалютному вкладу с учетом изменения обменного курса валют определяется по формуле:

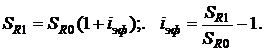
Откуда получим:

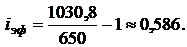
Если бы обменный курс валют не изменился, то наращенная сумма в рублях была бы равна:

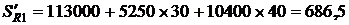тыс. руб.,

а эффективная процентная ставка составила бы:

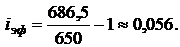
Если обменный курс валют не меняется, то эффективная процентная ставка равна средневзвешенному значению:

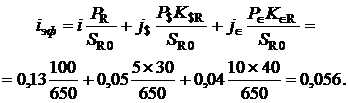
Последние шесть схем предполагают конвертацию валюты как в начале, так и в конце финансовой операции.

4. Для наращенной суммы по четвертой схеме получим:

- по депозитному договору с начислением простых процентов:

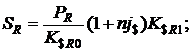(1.35)

- по депозитному договору с начислением сложных процентов:

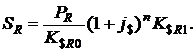(1.36)

Множители наращения в схеме простых и сложных процентов можно записать в виде:

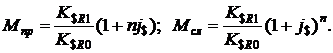(1.37)

Из приведенных формул видно, что множитель наращения увеличивается с повышением годовой процентной ставки и с ростом обменного курса доллара к концу срока депозита.

5. Для пятой схемы совершения финансовой операции:

Наращенные суммы по схеме простых и сложных процентов определяются формулами:

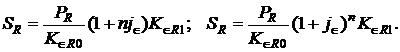(1.38)

Множители наращения для простых и сложных процентов будут соответственно равны:

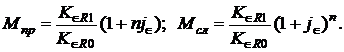(1.39)

Из формул (1.39) видно, что (как и в схеме 4) множитель наращения увеличивается с повышением процентной ставки и с ростом обменного курса евро к концу срока депозитного договора.

6. Для шестой схемы финансовой операции:

Наращенные суммы в долларах США при начислении простых и сложных процентов соответственно будут равны:

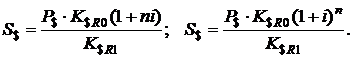(1.40)

Для множителей наращения при начислении простых и сложных процентов получим формулы:

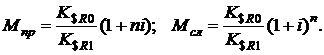(1.41)

7. Для седьмой схемы финансовой операции:

Наращенные суммы в евро при начислении простых и сложных процентов определяются формулами:

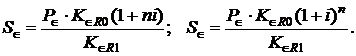(1.42)

Множители наращения при начислении простых и сложных процентов будут равны:

(1.43)

Из формул (1.41) и (1.43) видно, что множители наращения в шестой и седьмой финансовых схемах увеличиваются с повышением процентной ставки по депозиту и с уменьшением обменного курса евро к рублю к окончанию срока депозита.

8. Для финансовой операции, реализуемой по восьмой схеме:

Наращенные суммы в долларах США при начислении простых и сложных процентов можно определить по формулам:

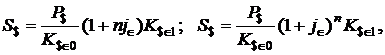(1.44)

где 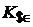- обменный курс долларов США в евро может быть рассчитан по формуле .

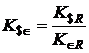Множители наращения для данной финансовой операции определяются формулами:

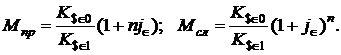(1.45)

Множители наращения финансовой операции по восьмой схеме увеличиваются при повышении процентной ставки и увеличении обменного курса 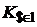к концу срока депозита.

9. Для финансовой операции, реализуемой по девятой схеме:

Наращенные суммы в евро при начислении простых и сложных процентов определяются формулам:

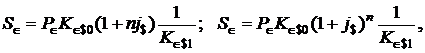(1.46)

где 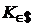- обменный курс покупки доллар США за евро, который может быть рассчитан по формуле .

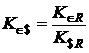Множители наращения в девятой схеме финансовой операции определяются формулами:

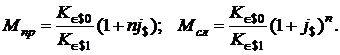(1.47)

Как следует из формул (1.47), множители наращения увеличиваются при повышении процентных ставок и снижении обменного курса евро в долларах США к окончанию срока депозитного договора.

Во всех схемах с конвертацией валюты наращенная сумма будет превышать первоначально вложенную сумму при M > 1. Из формул (1.47) следует, что множители ослабления будут больше единицы при соблюдении неравенств:

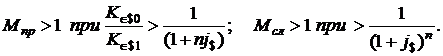
Аналогичные соотношения можно получить из формул (1.37), (1.39), (1.41), (1.43) и (1.45).

Контрольные вопросы и задания

1. Записать формулу для наращенной суммы при сроке депозита t дней с начислением процентов по схеме:

а) простых процентов;

б) сложных процентов.

2. Записать формулу для наращенной суммы при размещении средств S₀, последовательно вкладываемых на сроки n₁; n₂; ...; n_k с годовыми процентными ставками i₁; i₂; ..; i_k для случаев:

а) начисления простых процентов;

б) начисления сложных процентов.

3. На каком депозите будет более выгодным размещение средств при начислении простых процентов или при начислении сложных процентов при сроке депозита:

а) менее одного года;

б) более одного года.

4. Вычислить значение эффективной процентной ставки по депозиту при ежеквартальном начислении сложных процентов при годовой процентной ставке i = 12 %.

5. Какой вклад средств на депозит при начислении простых процентов более выгоден:

а) при однократном в год начислении процентов;

б) при ежеквартальном начислении процентов.

6. Пояснить понятия "математическое дисконтирование" и "банковский учет".

7. Привести формулы математического дисконтирования при размещении средств на срок t дней по схеме:

а) простых процентов;

б) сложных процентов.

8. Привести формулу математического дисконтирования при размещении средств по схеме сложных процентов на n лет с m-кратным начислением процентов.

9. Привести формулы дисконтирования при банковском учете векселей по схеме:

а) простых процентов;

б) сложных процентов.

10. Вексель стоимостью 100 тыс. руб. учитывается банком за 2 года до погашения по учетной ставке d = 10 %. Определить сумму средств, полученную векселедержателем, и дисконт банка при учете векселя:

а) по простой схеме дисконтирования;

б) по сложной схеме дисконтирования.

11. Записать формулу для реальной стоимости денежных средств в сумме S₀ по истечении одного года, если известны ежеквартальные темпы инфляции α₁; α₂; α₃; α₄.

12. Определить реально действующую с учетом инфляции ставку по депозиту, если годовая процентная ставка по депозиту i = 11 %, а годовой темп инфляции равен α_Σ = 8 %.

13. Определить, под какую годовую процентную ставку должен быть заключен депозитный договор, чтобы при годовой инфляции α = 8 % реально действующая с учетом инфляции процентная ставка составила не менее 5 %.

14. Определить реальную стоимость средств S₀ = 50 тыс. руб., размещенных в банке на полгода по схеме простых процентов с годовой процентной ставкой i = 12 % при ежемесячном темпе инфляции α_ср = 0,7 %.

15. Определить реальную стоимость средств S₀ = 40 тыс. руб., размещенных в банке на полтора года по схеме сложных процентов с годовой процентной ставкой i = 12 % при ежемесячном темпе инфляции α = 0,8 %.

16. Вклад помещен в банк под 18 % годовых. Найти эффективную процентную ставку по вкладу с учетом уплаты налога по ставке g_н = 35 % при ставке рефинансирования ЦБ России i_реф = 9 %.

17. В банке взят кредит под 19 % годовых. Найти эффективную процентную ставку по кредиту с учетом льготного налогообложения прибыли в части уплаты процентов по кредиту при ставке налога g_н = 20 % и ставке рефинансирования ЦБ России i_реф = 8 %.

18. Сумма 150 тыс. руб. положена в банк на валютный депозит в евро под j_? = 6 % годовых на полгода при начислении сложных процентов. Определить сумму, полученную в рублях, по окончании срока депозита, если обменный курс евро/руб. на момент заключения и окончания депозитного договора составил К₀ = 75 руб., К_t = 80 руб.

19. Сумма 5 тыс. долларов США положена в банк на рублевый депозит под i = 10 % годовых с ежеквартальным начислением сложных процентов. Определить сумму, полученную в долларах США по окончании срока депозита, если обменный курс $ - R на момент заключения и окончания депозитного договора составил К₀ = 70 руб., К_t = 65 руб.

20. В банке открыт мультивалютный вклад сроком на 1 год на суммы 100 тыс. руб. под 10,5 % годовых; 2000 долл. США под 5 % годовых; 5000 евро под 4 % годовых. Найти эффективную процентную ставку мультивалютного вклада, если курсы обмена валют в начале и в конце срока депозита были соответственно равны К_$R= (70 - 62), К_?R = (85 - 75).

Финансовые потоки, ренты

Основные понятия финансовых потоков

Финансовые потоки имеют широкое распространение на практике. Примерами финансовых потоков являются выплаты заработной платы, налоговые отчисления компании, коммунальные платежи, выплаты в погашение кредита, выплаты процентных доходов по депозитным договорам, ценным бумагам и т. п.

Графическое представление финансового потока приведено на рис. 2.1.

Рис. 2.1. Графическое представление финансового потока

Платеж Р, произведенный в некоторый момент времени t, называют финансовым событием, т. е. финансовое событие – это упорядоченная пара значений (Р, t), определяющих размер платежа Р и дату (время) платежа t.

Положительные платежи (со знаком плюс) означают поступление средств, отрицательные (со знаком минус) означают выплаты денежных средств.

Финансовые потоки могут быть как конечной последовательностью финансовых событий, так и бесконечной, они обозначаются символами CF (cash flow). Конечный финансовый поток, состоящий из (n + 1) финансовых событий, записывается в виде:

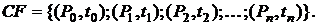
В общем случае платежи 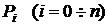могут быть различными по величине, интервалы времени между соседними платежами 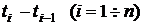и доходность 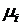финансовых операций на этих интервалах также могут принимать различные значения.

Как было показано в разделе 1, деньги должны работать и приносить доход. Денежные средства сегодня в размере 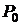через время 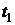с учетом возможного дохода могут иметь стоимость 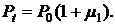Поэтому непосредственно суммировать размеры платежей 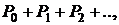совершаемых в разное время, некорректно. Для того чтобы вычислить величину потока в какой-то момент времени 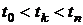, необходимо пересчитать все платежи от 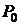до 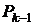с учетом их наращенной стоимости, а все платежи 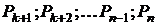дисконтировать к моменту времени 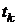. Сумма всех платежей финансового потока, приведенных к некоторому моменту времени 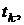называется текущим или приведенным значением потока и обозначается 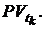При начислении дохода по сложной процентной ставке i% годовых для 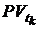можно записать:

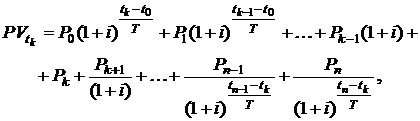(2.1)

где 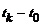- количество календарных дней с момента t₀ до t_k;

Т – количество дней в году;

i – годовая процентная ставка доходности.

Текущее значение потока в момент времени t₀ называется современной величиной потока и обозначается просто 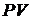без индекса:

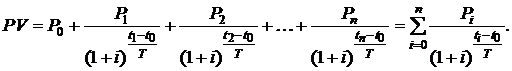(2.2)

Для момента t_n текущее значение потока называют конечным (накопленным) значением потока и обозначают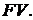

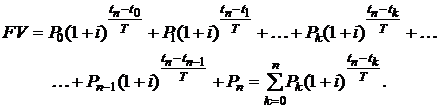(2.3)

Среди финансовых потоков важное место занимают потоки платежей через равные промежутки времени. Эти потоки называют финансовой рентой или просто рентой. Промежуток времени между двумя соседними платежами называется периодом ренты. Если в финансовой ренте, состоящей из n платежей, первый платеж совершается в момент времени t₀, а n-й платеж - в момент времени t_{n – 1} (рис. 2.3), то такую ренту называют авансовой, или пренумерандо. Если первый платеж совершается в момент времени t₁, а последний - в момент времени t_n (рис. 2.2), то такая рента называется обыкновенной, подрасчетной, или постнумерандо. Промежуток времени между началом первого периода t₀ и окончанием последнего периода t_n называется сроком ренты. Если все платежи равны между собой 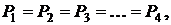то такую ренту называют постоянной.

Ренты описываются следующими параметрами: размером отдельного платежа, периодом и сроком ренты, процентной ставкой i, числом платежей в году r (r – срочные ренты), а также методом начисления процентов – простые и сложные, частотой m начисления процентов в году (m – кратные ренты).

В случае, когда период ренты равен одному году, такую ренту называют годовой, или аннуитетом (annuity). В русскоязычной финансовой литературе аннуитетом называют постоянную ренту с произвольным периодом.