Эквивалентность сложной процентной и сложной учетной ставок.

Исходные соотношения есть 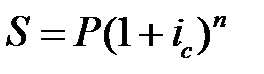и .

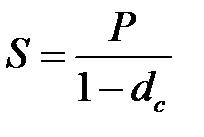Аналогично рассуждая, получим 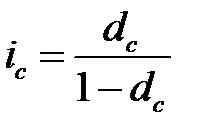и .

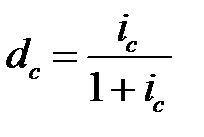Эквивалентность интенсивности процентов в единицу времени и ставок процентов. Интенсивность процентов δ в единицу времени удобно использовать в теоретических расчетах и обоснованиях финансовых решений. Из соотношений эквивалентности, можно перейти от непрерывного начисления процентов к дискретному, что более приемлемо на практике. Чаще возникает необходимость в соотношениях эквивалентности непрерывной и сложной ставок. Для эквивалентных сложных ставок δ,iи d имеем: .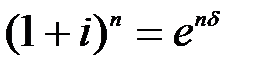

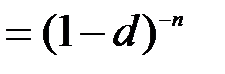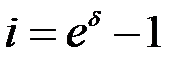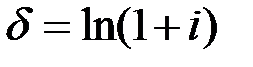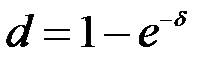Отсюда и ; и .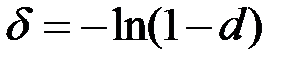

3. Средние величины в финансовых расчетах

Для нескольких процентных ставок их среднее значение есть эквивалентная величина.

Схема простых процентов. Пусть за периоды n₁, n₂, …, n_k начисляются простые проценты по ставкам i₁, i₂, …, i_k. Тогда за весь срок наращения n= n₁ + n₂ + …+ n_k средняя ставка простых процентов получается из уравнения эквивалентности 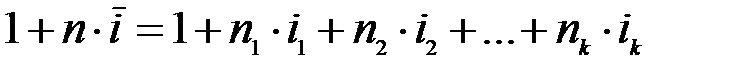. Откуда .

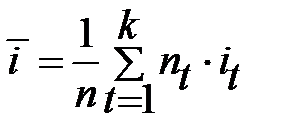Если же за время финансовой операции изменяется и величина P, то средняя ставка простых процентов равна .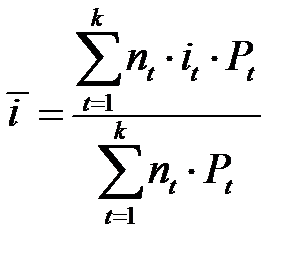

Аналогично средняя простая учетная ставка равна .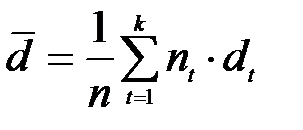

Средняя ставка 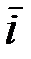( 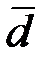) – это взвешенная средняя арифметическая величина, дающая такое наращение, которое эквивалентно наращению с применением ряда разных по значению процентных ставок, применяемых на различных интервалах времени.

Схема сложных процентов. Пусть доходность операции с дискретно изменяющейся процентной ставкой на каждом интервале начисления была выражена через сложный процент. Уравнение эквивалентности для определения средней процентной ставки, которая равноценна последовательности ставок за весь период финансовой операции, есть

.

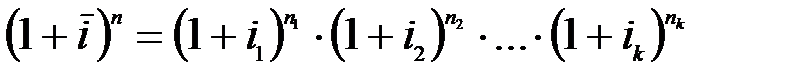Отсюда .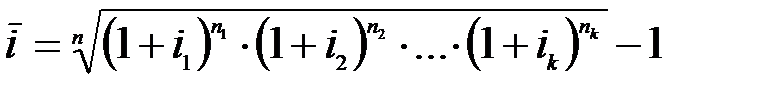

Следовательно, средняя сложная процентная ставка рассчитывается по формуле средней геометрической взвешенной.

Аналогично средняя сложная учетная ставка равна

.

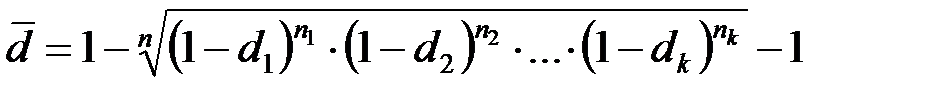Пример 4. Долгосрочный кредит предоставлен на 6 лет на следующих условиях: первые два года под 5 % (сложные проценты), в следующие три года ставка возрастает на 2 %, а в последний год – еще на 1 %. Определить среднюю сложную процентную ставку.

Решение. Параметры задачи: n₁ = 2 года, i₁ = 5 %, n₂= 3 года, i₂ = 7 %, n₃ = 1 год, i₃ = 8 %. Срок финансовой операции равен

n =n₁ + n₂ +n₃ = 2 + 3 + 1 = 6 лет.

Средняя ставка сложных процентов равна

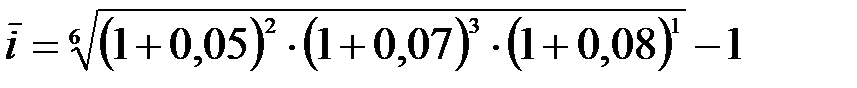= 0,064 9 или 6,49 %.

Таким образом, средняя процентная ставка по кредиту равна 6,49 %.

Вопросы для самопроверки:

1. Какие платежи считаются эквивалентными?

2. Что такое эквивалентная процентная ставка?

3. Что представляет собой финансовая эквивалентность обязательств?

4. Что такое средняя процентная ставка?

5. Что представляет собой процесс консолидирования задолженности?

Какая ставка считается критической?

Учет инфляции в финансово-экономических расчетах.