Общий подход к оценке акции. Модель постоянного дивиденда
Хотя точно предсказать цену акции с помощью формулы нельзя, можно установить ориентировочный уровень курса, вокруг которого теоретически цена должна изменяться.
Если доходы и расходы инвестора представить в виде диаграммы, то можно видеть, что цена акции должна быть равна дисконтированной сумме ожидаемых дивидендов по ней. Это может показаться странным, поскольку инвестор, вкладывая деньги в акции, часто надеется на прирост курсовой стоимости больше, чем на дивиденды. Однако поскольку единственный вид дохода, выплачиваемый по любой акции — это дивиденд, то и прирост курсовой стоимости, отражая изменение спроса на акции, в конечном счете отражает изменяющиеся перспективы относительно выплаты и размеров будущих дивидендов.
Для того чтобы акция приносила доход не ниже минимально допустимого при заданном уровне риска, необходимо, чтобы разовый платеж, т.е. выплата цены акции, компенсировался дисконтированной суммой дивидендов по данной акции. Если, например, дивиденды по привилегированной акции начисляются по фиксированной ставке, а срок существования корпорации и срок выпуска акции не ограничен, то такой поток дивидендов образует перпетуитет. Мы видели, что функция дисконтирования последовательности равных платежей Аnk при п 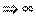 равна 1/k.
равна 1/k.
Модель DDM: P=d/k
Отсюда цена привилегированной акции Р равна:
P=d/k,
где d — ежегодный дивиденд по акции, ожидаемый в будущем, руб.;
k — ставка доходности по альтернативному вложению с таким же уровнем риска, как и риск вложения в данные акции, ден.ед.
Пример. Привилегированная акция номиналом 25 руб. выпущена со ставкой фиксированного дивиденда 30% годовых. Требуемый уровень доходности данной акции, соответствующий ее риску, составляет 35% годовых в рублях. По какому курсу будет продаваться данная акция (курс доллара США составляет 17,14 RUR/дол.)?
Расчетный рыночный курс данной привилегированной акции:
P = d/k =25х0,3/0,35 =21,43 руб.
Выраженная в долларах США цена привилегированной акции будет равна 21,43/17,14 = 1,25 дол. за акцию.
Предположим теперь, что дивиденд по акции непостоянен, а акция является обыкновенной. Возможно ли в этом случае подобным образом оценить ее курс?
Во-первых, если принять допущение, что дивиденд по акциям будет расти в соответствии с ростом цен, т.е. с инфляцией (а именно такой рост дивиденда по теории финансового менеджмента является оптимальным для стабильный компаний), то можно считать, что в реальной оценке дивиденд представляет собой постоянную величину, и тогда рыночная цена Р может быть рассчитана как сумма дивидендов, равных по величине, дисконтированных по реальной ставке альтернативной доходности. Тогда оценку курса можно сделать по модели DDM:
P=d/kp
где d — уровень дивиденда, ожидаемый в текущем периоде, ден. ед.;
kp — реальная ставка альтернативной доходности с таким же уровнем риска, как и данная акция, ден. ед.
DGM, или модель Гордона:
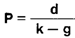
Во-вторых, если верно предположение о том, что можно;
ориентировочно оценить темп прироста дивиденда на единицу времени, то, считая его постоянным, нетрудно получить модель DGM, или формулу Гордона, которая в самом простом виде выглядит следующим образом:
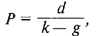
где g — темп прироста дивиденда;
d — ожидаемый дивиденд на следующий период;
k — ставка альтернативной доходности с таким же уровнем риска, как и данная акция. Данная формула получена путем дисконтирования последовательности платежей, имеющих постоянный темп прироста g.
Пример. Темп прироста дивиденда, переведенного в доллары США, по акции российской компании А за прошлые годы составлял:
g1=12% g2=8% g3=20% g4=12% g5 = 10% g6 = 22%
Дивиденд, ожидаемый в текущем периоде, равен 0,35 дол. на акцию. Оцените курс акции, если требуемый уровень ее доходности составляет, по рыночным данным, 23% годовых.(Примечание. В РФ акции чаще всего котируются в долларах США, а выплата дивидендов производится в рублях.).
Среднегодовой прирост дивиденда найдем по формуле средней геометрической, учитывая цепной характер индексов роста:
gcp = (1,12 х 1,08х 1,2х 1,12х 1,1 х 1,22) - 1 = 0,1388, или 13,88% годовых.
Курс акции определим по модели дивидендного роста:
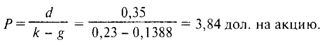
Стоимость долевого капитала корпорации. Выше было отмечено, что, хотя инвестор имеет возможность получить доход по своим акциям в форме дивиденда или в форме прироста их рыночной цены, прирост курса в конечном итоге объясняется теми доходами, которые будут по акции выплачены, т.е. будущими дивидендами. Поэтому требуемый уровень доходности со стороны инвестора в любом случае для эмитента является стоимостью, которую он выплачивает (раньше или позже) за пользование долевым капиталом.
Стоимость капитала согласно DGM:
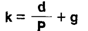
Пользуясь моделью Гордона (DGM), можно оценить, какую ставку выплачивает корпорация за пользование долевым капиталом акционеров. Действительно, модель показывает, какую цену надо заплатить за акцию, чтобы получить по ней уровень доходности, равный k. Однако если мы разрешим данное уравнение относительно k, то получим ответ на вопрос, какую ставку доходности платит инвесторам корпорация-эмитент по своим акциям, имеющим рыночную стоимость Р, ожидаемый дивиденд в текущем периоде d и среднегодовой прирост дивиденда g.
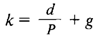
Пример. Рассмотрим ситуацию, изложенную в начале данного учебного элемента. По условию, капитал, полученный от размещения простых акций, по балансовой оценке составляет 800 220 тыс. руб., размещение происходило по номиналу 100 руб. за акцию, ожидаемый в текущем периоде дивиденд (d) — 12 руб. на акцию, среднегодовой прирост дивиденда (g) — 13% в год. Текущий рыночный курс (Р) — 116 руб. на акцию.
Следовательно, всего было выпущено:
800 220 тыс. руб./100руб. на акцию = 8 002 200 простых акций.
Стоимость капитала, полученного от их размещения:
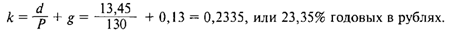
Рыночная стоимость всех этих акций (капитализация) в сумме составляет:
8 002 200 акций х 130 руб. на акцию = 1 040 286 тыс. руб. Капитал, полученный путем размещения безотзывных привилегированных акций по балансовой оценке, равен 216 530 тыс. руб., размещение происходило по номиналу 100 руб. за акцию, фиксированная ставка дивиденда 20% годовых, текущий рыночный курс (Р) — 105 руб. на акцию. Дивиденд по этим акциям фиксирован, следовательно, g = 0.
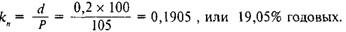
Количество этих акций в обращении:
216 530 тыс. руб./100 руб. на акцию = 2 165 300 привилегированных акций.
Их рыночная капитализация:
2 165 300 акций х 105 руб. на акцию = 227 356,5 тыс. руб.
Стоимость долевого капитала согласно САРМ:
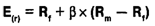
В предыдущем учебном элементе мы познакомились также с другим способом оценки стоимости долевого капитала. Требуемый инвесторами уровень доходности может быть определен в соответствии с состоянием финансового рынка и степенью систематического риска, количественно выражаемого коэффициентом:
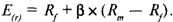
Пример. Вернемся к ситуации с АО «Энскэнерго», предложенной ранее. Известны следующие исходные данные:
| Ставка доходности с минимальным риском | 11,75% годовых |
| Среднегодовой прирост биржевого индекса | 21,02% годовых |
| Коэффициент систематического риска для корпорации | 1,07 |
Нетрудно, зная эти данные, определить требуемый акционерами — держателями обыкновенных акций уровень доходности (который одновременно является стоимостью капитала корпорации, полученного от размещения этих акций):