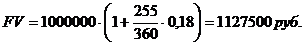Расчеты при начислении простых процентов

Начисление простых процентов может происходить дискретно в зависимости от условий договора раз в год, полугодие, квартал или месяц. Иногда проценты начисляют и за более короткий срок.

Пусть задана исходная стоимость денег 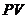. Наращенную (будущую) сумму денег через определенный период обозначим через ;

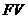Число процентных периодов, т.е. периодов начисления процентов - ;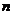

Ставку процентов за период- .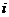

Тогда простые обычные проценты за один процентный период начисляются следующим образом: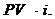

Следовательно, в конце первого процентного периода сумма денег составит .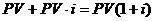

В конце второго процентного периода сумма увеличится еще на 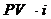и составит: .

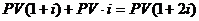В конце третьего - 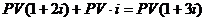и т.д.

Наконец, в конце n-го процентного периода наращенная сумма составит: .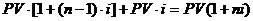

Таким образом, процесс наращения суммы денег за счет начисления простых процентов моделируется как арифметическая прогрессия с первым членом 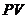и разностью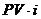

Следовательно, наращенная сумма денег за счет начисления простых процентов за 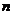процентных периодов времени имеет вид:

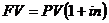(2.1)

Формулой (2.1) можно воспользоваться, например, для исчисления суммы погашения ссуды, предоставленной под простые проценты; размера срочного вклада с процентами и пр.

Множитель 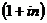называется множителем наращения простых процентов. Он показывает, во сколько раз увеличилась сумма вклада (или долга) к концу срока финансовой операции.

Сумма начисленных процентных денег может быть определена по формуле: 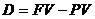. Разность 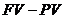называется дисконтом.

Пример. Вклад 100 000 рублей размещен в сберегательный банк на 3 года под обычные простые проценты 4,5 % годовых. Определите наращенную сумму вклада.

Решение: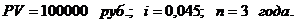

Найдем наращенную сумму вклада по формуле (5):

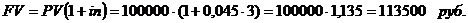
Наращение суммы вклада (процентные деньги) составит 13500 рублей.

В рассмотренном примере срок финансовой операции составляет 3 года. Однако, как правило, к наращению по простым процентам прибегают при выдаче краткосрочных ссуд, срок которых менее года (n<1). Рассмотрим более общий случай, когда n не является целым числом.

Отметим, что при использовании формулы (5) размерности n и ί должны быть согласованы. Если n измеряется в годах, то ί – ставка годовых процентов (показывает рост за год).

В случае если продолжительность финансовой операции не равна целому числу лет, периоды начисления процентов n выражают дробным числом, как отношение продолжительности финансовой сделки в днях к количеству дней в году (или отношение продолжительности финансовой сделки в месяцах к числу месяцев в году).

Обозначим срок операции 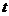(time), В качестве временной базы выберем продолжительность года, выраженную в тех же единицах, что и 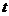.Обозначим ее 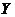(year-год). Подставим отношение 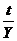вместо 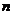в формулу (5), получим формулу (6)

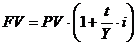(2.2)

Иногда при расчете простых процентов предполагают, что год состоит из 12 месяцев по 30 дней в каждом. Проценты, рассчитанные по временной базе Y=360 дней, называются обыкновенными или коммерческими процентами (ordinary interest). При использовании действительной продолжительности года (365 или 366 дней) получают точные проценты (exact interest).

Число дней финансовой операции также можно измерить приближенно и точно. В первом случае ее продолжительность определяется из условия, согласно которому месяц принимается равным 30 дням. Точное число дней финансовой операции определяется путем подсчета числа дней между датой ее начала и датой ее окончания по календарю. Первый и последний день финансовой операции считается за один день. На практике для подсчета ее продолжительности можно пользоваться табл. 1 и 2 (приложение 1). В таблицах приведены порядковые номера дней в году (для обычного и високосного годов соответственно). Срок проведения финансовой операции рассчитывается как разность между порядковыми номерами даты ее окончания и даты начала. Таким образом, на практике применяют три варианта расчетов:

1) Точные проценты с точным числом дней ссуды.

Этот вариант дает самые точные результаты. Онобозначается 365/365.Он применяется центральными банками многих стран и крупными коммерческими банками, например в Великобритании.

2) Обыкновенные проценты с точным числом дней ссуды.

Этот метод, иногда называемый банковским (Banker’s Rule), распространен в ссудных операциях коммерческих банков, в частности во Франции. Он обозначается как 365/360. Этот вариант дает несколько больший результат, чем применение точных процентов.

3) Обыкновенные проценты с приближенным числом дней ссуды.

Такой метод применяется тогда, когда не требуется большой точности, например при промежуточных расчетах. Он принят в практике коммерческих банков Германии. Этот метод обозначается как 360/360.

Вариант расчета с точными процентами и приближенным числом дней ссуды лишен смысла и не применяется.

Пример. Ссуда в размере 1 млн. руб. выдана 20 января до 5 октября включительно под 18 % годовых. Какую сумму должен заплатить должник в конце срока? Найти решение тремя способами.

Определим точное число дней ссуды. Дате 20 января соответствует № 20 (таблица 1 приложения 1). Дате 5 октября - № 278. Таким образом, точное число дней ссуды составит 258 дней (278 – 20).

Определим приближенное число дней ссуды. При этом продолжительность каждого месяца принимается за 30 дней. Количество полных месяцев срока ссуды равно 8 (с 20 января по 20 сентября). Срок от 20 сентября по 5 октября составляет 15 дней: (30-20)+5. Приближенное число дней ссуды рассчитывается таким образом: 8·30+15=240+15=255 дней.

Определим величину долга в конце срока тремя методами:

1.Точные проценты с точным числом дней ссуды (365/365):

=

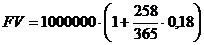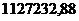
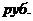
2. Обыкновенные проценты с точным числом дней ссуды (365/360)

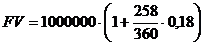
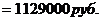
3. Обыкновенные проценты с приближенным числом дней ссуды (360/360)