ГЛАВА 1. Элементы экономико-математического моделирования

Содержание

Введение. 3

ГЛАВА 1. Элементы экономико-математического моделирования. 6

1.1. Линейное программирование. 6

1.2. Нелинейное программирование. 13

1.3. Стохастическое программирование. 17

ГЛАВА 2. Моделирование банковской деятельности. 24

2.1. Банк и банковская деятельность. 26

2.2. Основные направления оптимизационного моделирования банковской деятельности 33

2.3. Модели и задачи линейного и нелинейного программирования. 40

в банковской деятельности. 40

2.4. Постановка стохастической задачи. 42

2.5. Модели банка как совокупности стохастических финансовых процессов. 45

2.6. Исследование методов экономико-математического моделирования в прогнозировании деятельности кредитной организации. 54

ГЛАВА 3. Управление портфелем ценных бумаг в банковском бизнесе. 59

3.1. Основные стратегии эффективной деятельности банков. 59

3.2. Управление капиталом, активами и пассивами банка. 64

3.3. Управление портфелем ценных бумаг. 68

3.4. Формирование оптимального портфеля ценных бумаг. 81

Заключение. 88

Список использованной литературы.. 90

Приложения. 94

Введение

Цикличность в развитии экономических систем обязывает менеджмент банков адекватно реагировать на изменения экономической конъюнктуры для обеспечения устойчивости каждого банковского учреждения в отдельности и банковской системы в целом. Современные методики диагностики финансового состояния банка базируются на изучении, систематизации и обработке большого объема информации, содержащегося в официальной банковской отчетности ¹. Кроме того, алгоритмы расчетов показателей достаточно громоздки и не всегда очевидны, поэтому итоговые данные не могут в полной мере доступно и наглядно характеризовать финансовую устойчивость кредитной организации. Нивелировать эти недостатки и увеличить скорость реакции на изменения внешней среды, что определяет успех в управлении, позволяет математическое моделирование деятельности банка. Оно является основным элементом системы поддержки принятия решений, поскольку имеет самую малую среди других методов, способов и механизмов материалоемкость, а также позволяет подготовить и провести многочисленные эксперименты быстро и без социального риска.

Математическое моделирование в сфере банковской деятельности является практически не поддающимся научной формализации процессом. В 1972г. Мэрфи писал, что «трудно создать интегрированную теорию банковской фирмы, которая одновременно охватывала бы управление ликвидностью, выбор портфеля активов, политику ценообразования и физический процесс производства»². В связи с этим наибольшее

¹ Малюгин В. Оценка устойчивости банков на основе эконометрических моделей / Малюгин В., Пытляк Е. // Банковской вестник. - 2007. - №1. . – С.30-36.

² Murphy, Neil B. Costs of Banking Activities: Interactions Between Risk and Operating Costs: A comment / Murphy, Neil B. // Journal of Money, Credit and Banking. - 1972. . – August. - Р. 614-615.

распространение имеют либо частные модели, описывающие конкретную сферу деятельности банка, либо обобщенные полные модели, которые хотя и отображают функционирование банка в целом, но делают это достаточно агрегировано. Требования к комплексному подходу при моделировании банка сформулировал Балтенспергер: соотношение и структура требований и обязательств; размер собственного капитала банка ³. Традиционными являются стохастические и детерминированные модели, а также модели на основе теории нечетких множеств. Симбиоз этих подходов позволяет построить наиболее адекватную модель деятельности банка. Основанная на понятиях нечеткости, формализация неопределенности позволяет объединить достоинства точных и вероятностных моделей с субъективными данными и получить новые расчетные схемы, которые дают возможность изучать реальность без ее деформации.

Основным стержнем моделирования банковской деятельности является формирование разумных альтернатив его развития. При этом следует исходить из того, что, во-первых, банк - это фирма, деятельность которой связана с повышенными рисками, функционирующая в условиях неопределенности. Во-вторых, банк - это учреждение, стремящееся к повышению своей доходности. Соответственно этому, двумя основными факторами математического моделирования деятельности банка и стратегии его развития являются неопределенность и доходность. Таким образом, все известные модели деятельности банков не описывают в полной мере объект моделирования. Построение максимально полной по типам операций, по функциям модели, - основная задача математического моделирования деятельности банка.

Целью данной работы является детальное рассмотрение основных

³ Baltensperger, Ernst Alternative Approaches to the Theory of the Banking Firm / Baltensperger, Ernst // Journal of Monetary Economics. - 1980. . – №1 - Р. 1-37.

методов математического моделирования банковской деятельности и разработка специального программного обеспечения для реализации наглядного представления конкретной банковской задачи.

В первой главе необходимо рассмотреть общие теоретические задачи математического программирования, в том числе задача линейного и нелинейного программирования. Так же в первой главе поставлена задача стохастического программирования.

Вторая глава посвящена рассмотрению моделированию банковской деятельности, как в экономическом плане, так и в математическом. Необходимо привести детальное изучение и построение моделей линейного и нелинейного программирования, используемых в банковском бизнесе, так же выявить основные направления оптимизационного моделирования работы банка. Основной целью второй главы является изучение постановки стохастической задачи и рассмотрение модели банка как совокупности стохастических финансовых процессов.

В третье главе необходимо провести анализ проблемы построения оптимального портфеля ценных бумаг в банковском бизнесе и реализовать решение конкретной банковской задачи. В качестве написания практической части мною была выбрана задача построения оптимального портфеля ценных бумаг по заданным параметрам. Для написания программы необходимо использовать язык программирования Visual Basic for Applications.

В Заключении сформулированы основные полученные результаты и

выводы исследования.

Линейное программирование

Вычислительные методы, которые могут быть применены для эффективного расчета и анализа производственных планов, опираются на специализированный математический аппарат. Математическая база этих расчетов имеет название линейное программирование. Термин «программирование» нужно здесь понимать в значении «планирование». Он был предложен в середине 1940-х годов Джорджем Данциг, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации.

Линейное программирование рассматривает условия принятия решений посредством линейных функций, линейных уравнений и неравенств. Оно даёт возможность в достаточно простой и математически форме разделить допустимые и недопустимые решения, рассмотреть множество допустимых значений и однозначно дать ответ на вопрос о существовании или не существовании оптимального решения. Если такое оптимальное решение существует, то методы линейного программирования позволяют его отыскать. Соответствующие расчеты и анализ полученных результатов могут быть проведены на компьютере.

Рассмотрим постановку задачи линейного программирования на примере, приведенном Б. Банди в своей работе «Основы линейного программирования» . ⁴ Автор рассматривает фирму, которая производит два типа книжных полок А и В. Наличие сырья (высококачественные доски) и время машинной обработки ограничивают производство. Для каждого изделия типа А требуется 3 м² досок, а для изделия типа В – 4 м².

Поставщики доставляют фирме до 1700 м² в неделю. Для каждого изделия типа А требуется 12 минут машинного времени, а для изделия типа В – 30 минут. В неделю можно использовать 160 ч машинного времени. Главная задача фирмы состоит в определении сколько книжных полок каждого типа необходимо выпускать в неделю, если каждое изделие типа А приносит 2$ прибыли, а каждое изделие типа В – 4$ прибыли?

Для постановки математической модели задачи введем следующие

⁴ Банди Б. Основы линейного программирования: Пер. с англ. – М.: Радио и связь, 1989. – 8-11- с.: ил.

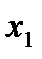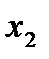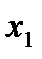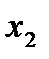обозначения: через обозначим количество выпущенных за неделю книжных полок типа А, а через – количество выпущенных книжных полок типа В. Задача состоит в том, чтобы найти наилучше значения и . Нетрудно видеть, что наилучшими для данной задачи являются значения, максимизирующие еженедельную прибыль. Еженедельная прибыль есть следующие выражение:

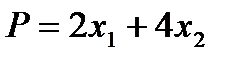(1.1.1)

Фирма будет получать максимальную еженедельную прибыль, если максимизируется целевая функция _.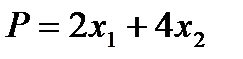

В соответствии с классической теории оптимизации экстремумы функции достигаются в точках, в которых обращаются в ноль ее производные, либо на границе области определения. Изучение производных в рассматриваемом примере недостаточно, так как

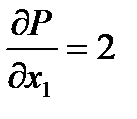и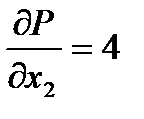

и никаким выбором 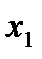и 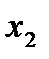нельзя обратить эти производные в ноль. Действительно, чтобы увеличить функцию 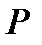, надо увеличить 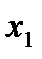и 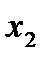. Но значения 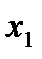и 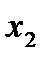не могут быть увеличены неограниченно. Это ограничения на количество сырья и машинное время.

Так как 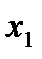и 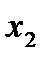выражают еженедельный объем выпуска, то они не могут быть отрицательны, т. е.

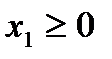и 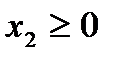. (1.1.2)

Следовательно, ограничения на количество досок и машинное время могут быть записаны следующим образом:

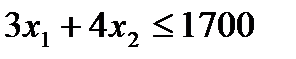(для досок),

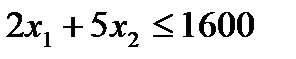(для машинного времени). (1.1.3)

Задача состоит в том, чтобы найти значения 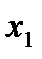и 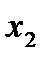, удовлетворяющие условиям неотрицательности (1.1.2) и ограничениям в виде неравенств (1.1.3) и максимизирующие целевую функцию _.

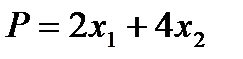Это типичная двухмерная задача линейного программирования. Целевая функция, которая должна быть максимизирована, является линейной функцией своих переменных. Также линейными являются и ограничения на эти переменные. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта. Границы определяются прямыми

,

.

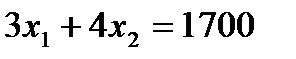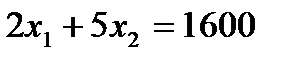Стрелками на каждой границе рис. 1.1.1. показано, с какой стороны выполнено ограничение. Заштрихованная область ОАВС, содержащая точки, для которых соблюдены условия (1.1.2) и (1.1.3), называется допустимой. Точки внутри и на границе этой области изображают допустимые решения. Допустимых значений много. Задача состоит в том, чтобы найти решение, максимизирующее функцию 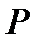среди множества допустимых значений.

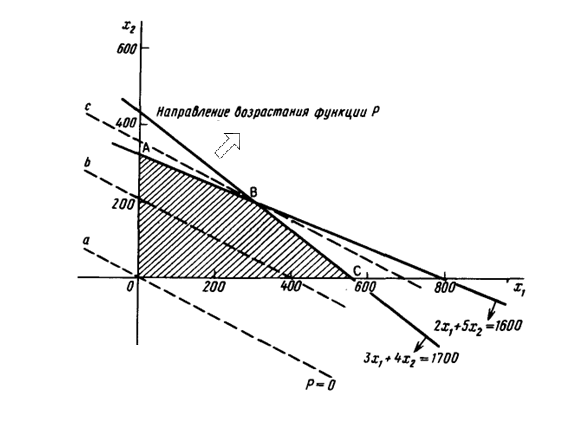
Рис. 1.1.1. Графическая постановка задачи линейного программирования

Штриховыми линиями на рис. 1.1.1. изображены прямые 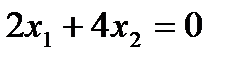, , 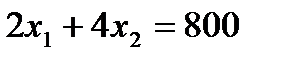обозначенные a и b соответственно. Эти прямые параллельны и представляют собой две линии уровня функции 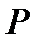со значениями соответственно 0 и 800. Ясно, что значение функции 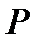возрастает по мере того, как линии уровня удаляются от начала координат в положительном квадранте. Действительно, вектор с компонентами 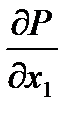, , 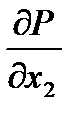т. е. вектор с компонентами 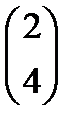указывает направление возрастания функции 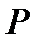, перпендикулярен штриховым линиям и направлен в сторону, противоположную началу координат.

Линией уровня с наибольшим значением функции 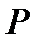, имеющей хотя бы одну общую точку с допустимой областью, является прямая , проходящая через вершину В; на ней 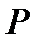принимает значение 1400. Точка В, в которой 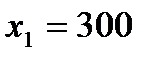, , 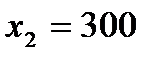соответствует оптимальному решению задачи. Эти значения могут быть получены как решения уравнений

,

.

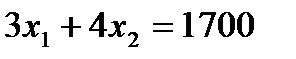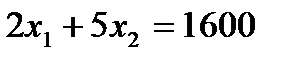Следовательно, максимальная прибыль составляет 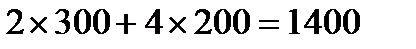. При оптимальном решении оба ограничения превращаются в равенства, что означает полное использование сырья и машинного времени.

Рассмотренная задача может быть расширена до трёх и более моделей и соответствующего количества неотрицательных переменных. Могут быть введены дополнительные ограничения, связанные с возможностями рынка, упаковкой и т.д. В этом случае задача по прежнему заключается в максимизации линейной функции от нескольких неотрицательных переменных с линейными ограничениями в форме неравенств.

Общая задача линейного программирования состоит в оптимизации (нахождение максимума или минимума) линейной функции

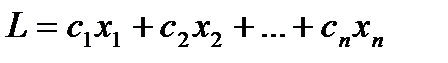(1.1.4)

от 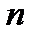вещественных переменных 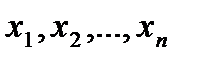, удовлетворяющих условия неотрицательности

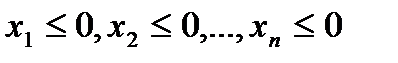(1.1.5)

и 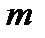линейными ограничениями

,

,

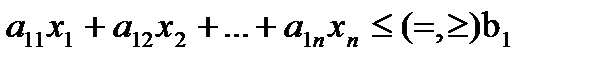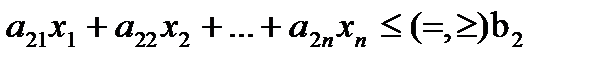……………………………… (1.1.6)

.

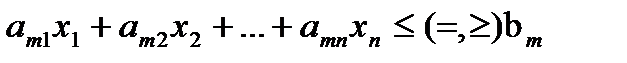Среди ограничений могут одновременно встречаться знак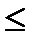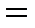и , и 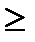. Задача состоит в максимизации (минимизации) целевой функции. Значения 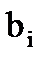, , 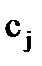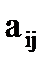предполагаются известными.

В матричных обозначениях задача может быть представлена следующим образом (под векторными неравенствами подразумевается выполнение всех неравенств покоординатно): максимизировать (минимизировать) функцию

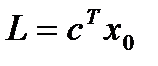(1.1.7)

где

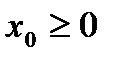, (1.1.8)

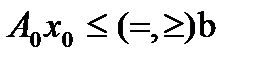, (1.1.9)

и

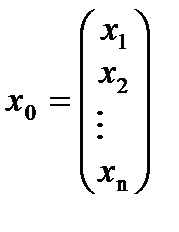- вектор- столбец ,

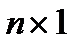а

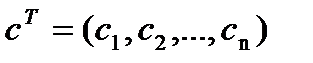- вектор-строка ,

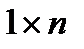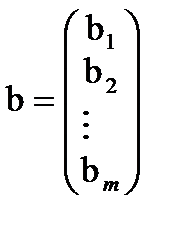- вектор-столбец ,

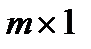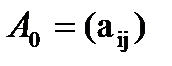- матрица .

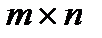Индекс 0 в векторе 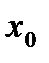и в матрице 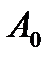указывает на то, что это начальные значения.

Нелинейное программирование

В предыдущем пункте была рассмотрена задача линейного программирования. Существует множество примеров, которые показывают, что многие практические проблемы можно сформулировать математически как задачу линейного программирования. Однако имеются проблемы, в которых связи заведомо не являются линейными. Таковы, например, задачи увеличения масштабов производства, перехода на новую технологию, оптовой торговли и т.д. Поэтому ясна необходимость изучения нелинейных моделей и методов их анализа. Модели эти, конечно, сложнее линейных и разработанные для них методы менее эффективны, чем методы решения линейных задач.

Нелинейное программирование - случай математического программирования, в котором целевой функцией или ограничениями является нелинейная функция. Общая задача нелинейного программирования имеет вид: оптимизировать функцию 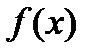при условиях

,

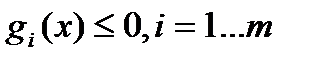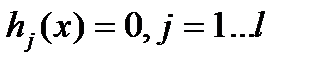, (1.2.1)

.

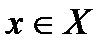Здесь 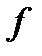, , 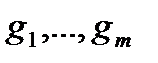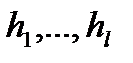- функции, определенные на 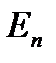(совокупность всех векторов размерности 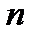образует 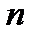- мерное евклидово пространство, которое обозначается 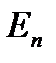), 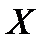- множество из 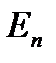, 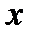- вектор с компонентами 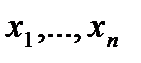. Задача заключается в нахождении переменных 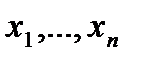, удовлетворяющих ограничениям и отвечающих при этом минимальному значению функции .

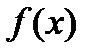Функцию 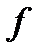обычно называют целевой функцией, или критерием оптимальности. Каждое условие 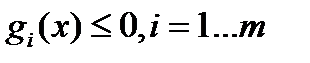называют ограничением-неравенством или ограничением в форме неравенства, а условие вида 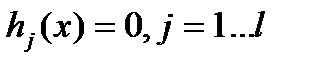- ограничением-равенством или ограничением в форме равенства. Вектор 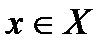, удовлетворяющий всем ограничениям, называют допустимым решением, или допустимой точкой. Совокупность всех допустимых точек образует допустимую область. Таким образом, задача нелинейного программирования заключается в нахождении такой допустимой точки 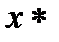, для которой 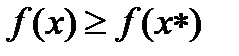при всех допустимых решениях 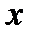. Точка 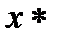называется оптимальным решением или просто решением задачи. В отличие от задачи линейного программирования в задаче нелинейного программирования оптимум не обязательно лежит на границе области, определенной ограничениями.

Рассмотрим некоторые методы решения задач нелинейного программирования. Одним из методов, которые позволяют свести задачу нелинейного программирования к решению системы уравнений является метод неопределенных множителей Лагранжа.

Если целевая функция является вогнутой (задача максимизации), или выпуклой (задача минимизации) и множество ограничений является выпуклой, то задачу называют выпуклой и в большинстве случаев могут быть использованы общие методы выпуклой оптимизации.

Если целевая функция является отношением вогнутых и выпуклых функций (при максимизации) и ограничения выпуклые, то задача может быть преобразована в задачу выпуклой оптимизации использованием техник дробного программирования.

Существуют несколько методов для решения невыпуклых задач. Один подход заключается в использовании специальных формулировок задач линейного программирования. Другой метод предусматривает использование методов ветвей и границ, где задача делится на подклассы, чтобы быть решенной с выпуклыми (задача минимизации) или линейными аппроксимациями, которые образуют нижнюю границу общей стоимости в пределах раздела. При следующих разделах в определенный момент будет получено фактическое решение, стоимость которого равна лучшей нижней границе, полученной для любого из приближенных решений. Это решение является оптимальным, хотя, возможно, не единственным. Алгоритм можно прекратить на ранней стадии, с уверенностью, что оптимальное решение находится в рамках допустимого отклонения от найденной лучшей точки. Завершение такой оптимальной точки, как правило, необходимое для обеспечения конечности завершения. Это особенно полезно для больших, сложных задач и задач с неопределенными расходами или значениями, где неопределенность может быть определена из соответствующей оценки надежности.

Рассмотрим общую задачу оптимизации, содержащую несколь­ко ограничений в виде равенств: минимизировать

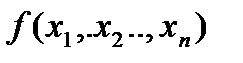(1.2.2)

при ограничениях

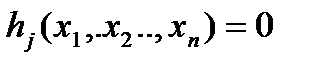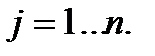, (1.2.3)

Эта задача в принципе может быть решена как задача безусловной оптимизации, полученная путем исключения из целевой функции 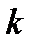независимых переменных с помощью заданных равенств. Наличие ограничений в виде равенств фактически позволяет уменьшить размерность исходной задачи с 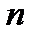до .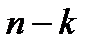

Подробней остановимся на методе неопределенных множителей Лагранжа. Это метод нахождения условного оптимума, предложенный итальянским математиком Жозефом-Луи Лагранжем. Метод позволяет свести задачу на отыскание условного оптимума к задаче на нахождение безусловного оптимума.

С помощью метода множителей Лагранжа по существу устанавливаются необходимые условия, позволяющие идентифицировать точки оптимума в задачах оптимизации с ограничениями в виде ра­венств. При этом задача с ограничениями преобразуется в эквива­лентную задачу безусловной оптимизации, в которой фигурируют некоторые неизвестные параметры, называемые множителями Ла­гранжа.

Рассмотрим задачу минимизации функции 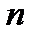переменных с уче­том одного ограничения в виде равенства: минимизировать 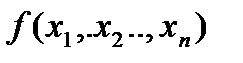при ограничениях

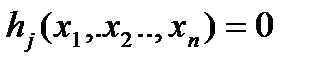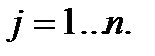, (1.2.4)

В соответствии с методом множителей Лагранжа эта задача преобразуется в следующую задачу безусловной оптимизации: минимизировать

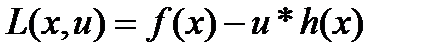(1.2.5)

Функция 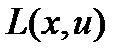называется функцией Лагранжа, 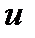— неизвест­ная постоянная, которая носит название множителя Лагранжа. На знак 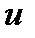никаких требований не накладывается.

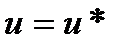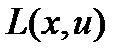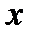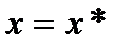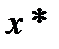Пусть при заданном значении безусловный минимум функ­ции по достигается в точке и удовлетворяет урав­нению 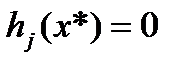. Тогда, как нетрудно видеть, 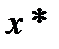минимизирует 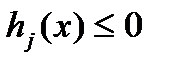с учетом (1.2.4), поскольку для всех значений 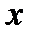, удовлетворяющих (1.2.4), 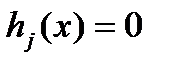и .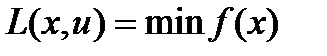

Разумеется, необходимо подобрать значение 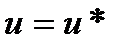таким обра­зом, чтобы координата точки безусловного минимума 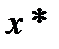удовлетво­ряла равенству (1.2.4). Это можно сделать, если, рассматривая 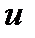как переменную, найти безусловный минимум функции (1.2.5) в виде функции 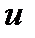, а затем выбрать значение 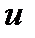, при котором выполняется равенство (1.2.4).

В банковской деятельности

Ответственные решения в современных целенаправленных системах планирования и управления должны быть в некотором смысле экстремальными или близкими к ним. Отступление от этого принципа обычно связано с излишними затратами (часто весьма значительными) и снижает эффективность управления (часто весьма существенно).

При моделировании банковской деятельности часто приходится сталкиваться с задачей математического программирования, которая может быть сформулирована следующим образом: найти значения переменных 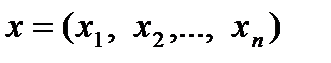, которые удовлетворяют неравенствам

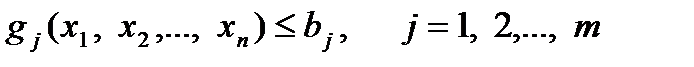(2.3.1)

и обращают в минимум (максимум) функцию :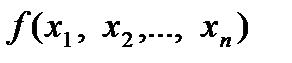

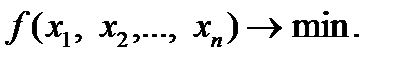(2.3.2)

Вид функци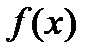й и 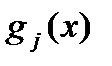определяет класс задач математического программирования. Если все функции 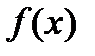, , 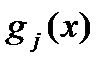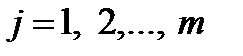линейны, получаем задачу линейного программирования. Если хотя бы одна из функций нелинейна, имеем задачу нелинейного программирования.

Классические методы поиска экстремума в задачах нелинейного программирования тесно связаны с понятием выпуклой функции, седловой точки, необходимыми и достаточными условиями экстремума (теорема Куна-Таккера), функцией и множителями Лагранжа

План, набор команд управления или проект часто могут быть формально представлены в виде системы чисел или функ­ций, удовлетворяющих определенным ограничениям — равен­ствам, неравенствам или логическим соотношениям. План, си­стема команд управления или проект оптимальны, если они, кроме того, обращают в минимум или в максимум (в зависи­мости от постановки задачи) некоторую функцию от искомых параметров — показатель качества решения.

Записи (2.3.1), (2.3.2), вполне осмысленные при детерминиро­ванных значениях параметров условий задачи, теряет опреде­ленность и требует дополнительных разъяснений при случайных значениях исходных данных. Между тем во многих прикладных задачах коэффициенты целевой функции, элементы функции условий или составляющие вектора ограничений — случай­ные величины.

Исходная информация для планирования, проектирования и управления в экономике, как пра­вило, недостаточно достоверна. Планирование производства обычно ведется в условиях неполной информации об обстановке, в которой будет выполняться план и реализовываться произ­веденная продукция. Во всех случаях в моделях математического программирования, к исследованию которых сводятся задачи планирования, проектирования и уп­равления, отдельные или все параметры целевой функции и ограничений могут оказаться неопределенными или случай­ными, Естественный на первый взгляд путь анализа подобных задач—замена случайных параметров их средними значениями и вычисление оптимальных планов полученных таким образом детерминированных моделей—не всегда оправдан. При сгла­живании параметров условий задачи может быть нарушена адекватность модели изучаемому явлению. Усреднение исходных данных может привести к потере полезной информации и привнести в модель ложную информацию. Решение детерми­нированной задачи с усредненными параметрами может не удовлетворять ограничениям исходной модели при допустимых реализациях параметров условий.

Рекомендации по выбору эффективного портфеля

Ценных бумаг

Способность ЛПР по выбору ценных бумаг	Способность ЛПР предсказать состояние рынка ЦБ
	хорошая	Плохая
Хорошая	1. Сконцентрировать средства в выбранных ценных бумагах без диверсификации
2. Сместить коэффициент β выше или ниже желаемого долгосрочного уровня основанного на прогнозе рынка	2. Держать коэффициент β на желаемом долгосрочном уровне
Плохая	1. Создать девирсифицированный портфель	1. Создать максимально девирсифицированный портфель
2. Сместить коэффициент β выше или ниже желаемого долгосрочного уровня основанного на прогнозе рынка	2. Держать коэффициент β на желаемом долгосрочном уровне

1. Пассивное управлениебазируется на предположении, что рынок достаточно эффективен для достижения успеха в подборе ценных бумаг или в учете времени и не следует забегать вперед (как при активном управлении). Суть тактики пассивного управления состоит в создании хорошо диверсифицированного портфеля с заранее заданными уровнями риска и в сознательном поддержании стабильного состояния портфеля ценных бумаг (они характеризуются, как правило, низким оборотом, минимумом накладных расходов и низким уровнем рисков). Важнейшим элементом при этом является создание индексного фонда, обеспечивающего контроль за риском и нормальную деятельность портфеля (индексный фонд — это портфель, зеркально отображающий движение выбранного индекса, характеризующего состояние фондового рынка; если доля 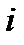-й компании при подсчете индекса Доу—Джонсона составляет, к примеру, 10%, то инвестор, стремящийся к созданию портфеля ценных бумаг, адекватно отображающего состояние всего рынка ценных бумаг, должен также иметь в своем активе 10% акций данной компании из общего числа ценных бумаг портфеля).

Другим методом пассивного управления выступает метод сдерживания портфелей,суть которого состоит в инвестировании в неэффективные ценные бумаги, когда выбираются акции с минимальным соотношением цены к доходу, позволяя получать доход от спекулятивных операций на бирже (при падении цены их покупают, а при росте цены их продают).

2. Активное управлениепортфелем ценных бумаг основано на использовании сложных технологий сокращения риска и применении форвардных сделок, опционов, фьючерсов и свопов.

Своповые операциипри активном управлении портфелем ценных бумаг применяются с целью предотвратить обесценение портфеля активов. Классический своп— это взаимодействие дилеров на фондовом рынке, придерживающихся различных позиций по тенденциям изменения процентных ставок и их влияния на будущую стоимость ценных бумаг, выбору набора кратко-, средне- или долгосрочных операций, обусловливающего получение высокой прибыли. Операции свопинга означают постоянный обмен, ротацию ценных бумаг через финансовый рынок с использованием операций, основанных на продвижении учетной ставки, «подмены», «сектор-свопа» и др. Например, свопинговые операции «подмена» базируются на том, что обмениваются две похожие, но не идентичные ценные бумаги. Например, облигации компании ABC с 15%-ным доходом и сроком погашения 10 лет и облигации финансовой компании на 8 лет с 10% дохода, причем первая ценная бумага продается на 10 пунктов больше, чем вторая. Менеджер, имеющий ценные бумаги второго вида, может провести свопирование ценных бумаг первого вида, так как 10 пунктов добавочного дохода с продлением срока действия облигации на два года являются довольно высокой прибавкой.

Довольно сложные операции «сектор-свопа» обеспечивают перемещение ценных бумаг из разных секторов экономики с различным сроком действия, доходом и т. п., а также ценных бумаг, отличающихся своими показателями от бумаг со средними показателями. При получении информации об исчезновении факторов, вызывающих эти отличия в характеристиках ценных бумаг, банк может осуществлять оперативные операции купли-продажи. В целом операции свопинга позволяют практически устранять такие виды рисков, как селективный, процентный, временной, инфляционный, но при условиях качественной проработки и выбора наилучшей стратегии банка и долгосрочных прогнозов состояния финансового и фондового рынков.

Заключение

Широкое внедрение электронно-вычислительной техники во все сферы нашей жизни в последнее время, вызвало бурный рост технологий, связанных с применением в них средств вычислительной техники. Одной из наиболее крупных отраслей развития технологий с применением ЭВМ, является математическое моделирование, которое достаточно просто (в отличие от аналогового моделирования) может быть реализовано на ЭВМ разных модификаций и возможностей. Связано это с тем, что при математическом моделировании модель представляет собой определенную последовательность математических зависимостей и динамика такой модели представляет собой изменение параметров зависимостей в результате выполнения расчетов. Математическое моделирование тесно связано с имитационным моделированием. Одним из разделов математического моделирования, являются модели систем массового обслуживания и их изучение.

В данной дипломной работе были рассмотрены методы прикладной математике, применяемые в моделировании банковской деятельности. Большинство распространенных математических технологий тем или иным образом воплощены в информационных технологиях.

Информационные системы являются комплексом моделей предметной области (реального или виртуального мира). Информационные системы могут включать в себя в качестве компонент (подмоделей) как базы данных, так и математические, логические, имитационные модели объектов и/или процессов.

Кроме того, широко распространены программные продукты (пакеты прикладных программ), поддерживающие (и поддерживаемые) определенные информационно-математические технологии. Например, модели системной динамики (глобального моделирования), программы статистической обработки и регрессионного анализа (построения статистических моделей), программные средства экономико-математического моделирования, информационно-поисковые и информационно-логические системы и пр.

По всей видимости, серьезные исследования исторических, демографических, экологических, экономических и пр. процессов невозможны без использования в качестве информационного и математического обеспечения баз данных и пакетов прикладных программ.

В дипломном проекте мною были рассмотрены и решены многие задачи математического моделирования банковской деятельности, поставленные в начале работы. Произведено исследование методов экономико-математического моделирования в прогнозировании деятельности кредитной организации. Обобщая проведенную работу, считаю, основные проблемы в сфере банковского дела и связа