Определение величины периодического платежа. Функция ПЛТ()

Пример 3‑6

Решим предыдущую задачу, используя функцию ПЛТ()

Разместим исходные данные задачи в таблице подобной приведенной на рисунке.

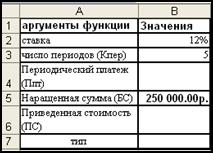
Рис. 3‑12 Таблица Excel с исходными данными задачи

Для решения задачи:

Установить курсор в ячейку В4(Плт).

Из категории функций «Финансовые» вызвать функцию ПЛТ().

В диалоговом окне функции сделать необходимые ссылки на ячейки таблицы исходных данных

Щелкнуть на кнопке «ОК»

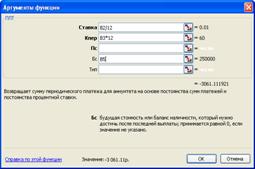
Рис. 3‑13 Диалоговое окно функции ПЛТ()

В результате выполненных действий в ячейке «В4» будет размещена найденная сумма ежемесячного платежа.

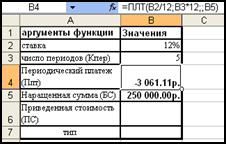
Рис. 3‑14 Таблица исходных данных с найденной величиной ежемесячного платежа (ячейка В4)

Пример 3‑7

Как только Вам исполнилось 20 лет Вы решили ежемесячно вносить в банк по 25 долларов США.

В каком возрасте Вы сможете стать миллионером, если ставка банка – 15%, начисляемых ежемесячно по схеме сложных процентов.

Решение.

Для решения задачи может быть использована финансовая функция КПЕР().

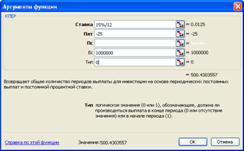
Рис. 3‑15 Диалоговое окно функции КПЕР()

В строку«Ставка»диалогового окна функции КПЕР() заносится величина годовой процентной ставки, деленной на количество платежей в течении года ( в нашей задаче –12 платежей).

В строку «Плт» заносится величина ежемесячных платежей

В строку «Бс» заносится величина будущей наращенной суммы ( в нашей задача 1000000 руб.

После щелчка на кнопке «ОК» в ячейку, где была размещена формула, будет занесено количество платежей, необходимых для накопления желаемой суммы = 500.43.

Т.е. через 500.43месяцев или 500.43/12 = 41,7 года Вам потребуется для накопления суммы 1000000 долларов США. Таким образом, Когда Вам исполнится 62 года Вы станете миллионером!

Расчет платежей по процентам. Функция ПРПЛТ()

Функция позволят определить сумму платежей процентов по инвестиции за данный период на основе постоянства сумм периодических платежей и постоянства процентной ставки.

Пример 3‑8

Необходимо определить величину платежей по процентам за первый месяц трехгодичного займа в 800тыс.руб. Ставка банка 10%.

Решение.

=ПРПЛТ(10%/12;1;3*12;-800)

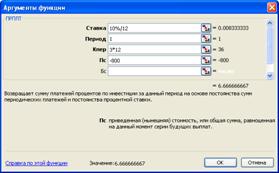
Рис. 3‑16 Диалоговое окно функции ПРПЛТ() с решением примера 3-10

ðВ поле «Ставка» диалогового окна заносится величина месячной процентной ставки;

ðв поле «Период» заносится номер периода для которого мы хотим определить величину платежей по процентам;

ðв поле «Кпер»заносится количество периодов начисления процентов ( в нашем примере 3*12);

ðв поле «Пс» заносится величина займа.

После нажатия кнопки «ОК» мы получим, что платежи по процентам за первый месяц составили -6.66 тыс. руб

Пример 3‑9

За счет ежегодных отчислений в течении 6 лет был создан фонд в 5 млн. руб.

Необходимо определить какой доход принесли вложения за последний год, если ставка банка составляла 12%

Решение

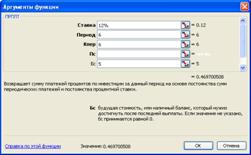=ПРПЛТ(12%;6;6;;5) =0,469млн. руб

Рис. 3‑17 Решение

примера 3-11