Характеристики финансовых потоков

В основе процесса принятия управленческих решений инвестиционного характера лежит оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Общая логика анализа с использованием формализованных критериев в принципе достаточно очевидна — необходимо сравнивать величину требуемых инвестиций с прогнозируемыми доходами.

Как уже говорилось, инвестиционные проекты, результаты применения управляющих воздействий к процессам налогообложения и другие экономические реалии описываются финансовыми потоками (потоками платежей и поступлений), т.е. функциями (временными рядами), а сравнивать функции естественно с помощью тех или иных характеристик (критериев).

Период возврата капиталовложений

Чистая кумулятивная текущая стоимость

Период производства продукции

Рис.1. Типовой финансовый профиль инвестиционного проекта.

Типовой график финансового потока инвестиционного проекта (как говорят, финансовый профиль инвестиционного проекта) представлен на рис.1.

Критерии (показатели, характеристики финансовых потоков), используемые при анализе инвестиционной деятельности, можно подразделить на две группы в зависимости от того, учитывается или нет временной параметр: а) основанные на дисконтированных оценках; б) основанные на учетных (номинальных) оценках. К первой группе относятся критерии:

чистая текущая стоимость (Net Present Value, NPV);

индекс рентабельности инвестиции (Profitability Index, PI);

внутренняя норма доходности (Internal Rate of Return, IRR);

модифицированная внутренняя норма доходности (Modified Internal Rate of Return, MIRR);

дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP).

Ко второй группе относятся:

срок окупаемости инвестиции (Payback Period, PP);

коэффициент эффективности инвестиции (Accounting Rate of Return, ARR).

Чистая текущая стоимость. Этот критерий основан на сопоставлении величины исходных инвестиций (IС) с общей суммой дисконти­рованных чистых денежных поступлений, генерируе­мых проектом в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента q, устанав­ливаемого аналитиком (выступающим от имени инвестора) самостоятельно исходя из ежегодного процента возврата, который инвестор хочет или может иметь на инвестируемый им капитал.

Допустим, делается прогноз, что исходные инвестиции (IС) бу­дут генерировать в течение n лет годовые доходы в размере Р₁, Р₂, ... , P_n. Общая накопленная величина дисконтированных доходов (Present Value, PV, т.е. доход, выраженный в неизменных ценах, приведенный к текущему моменту) и чис­тая текущая стоимость (Net Present Value, NPV, т.е. чистая приведенная величина) соответственно рассчитываются по формулам:

n P_k

PV = å ¾¾¾ ,

^k=1 (1+q)^k

и

n P_k

NPV = å ¾¾¾ - IC .

^k=1 (1+q)^k

Очевидно, что если:

NPV > 0, то проект целесообразно принять;

NPV < 0, то проект целесообразно отвергнуть;

NPV = 0, то проект ни при­быльный, ни убы­точный.

Теперь дадим экономическую интерпретацию значению критерия NPV с позиции владельцев компании:

• если NPV < 0, то в случае принятия проекта ценность компании уменьшится, т.е. владельцы ком­пании понесут убыток;

• если NPV = 0, то в случае принятия проекта ценность компании не изменится, т.е.благосостояние ее владельцев останется на прежнем уровне;

• если NPV > 0, то в случае принятия проекта ценность компании, а следовательно, и благосостоя­ние ее владельцев увеличатся.

При прогнозировании доходов по годам необходи­мо по возможности учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с дан­ным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высво­бождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.

Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ре­сурсов в течение т лет, то формула для расчета NPV модифицируется следующим образом:

_n P_{k m} IC_j

NPV = å ¾¾¾ - å ¾¾¾ ,

^k=1 (1+q)^{k j=1} (1+q)^j

где q,- дисконт-фактор.

Необходимо отметить, что показатель NPV отражает прогнозную оценку изменения экономического по­тенциала организации в случае приня­тия рассматриваемого проекта. Этот показатель адди­тивен в пространственно-временном аспекте, т.е. NPV различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.

Как уже отмечалось, не всегда инвестиции сводятся к одномоментному вложению капитала, а возврат происходит равными порциями. Чаще приходится анализировать поток платежей и поступлений общего вида. Будем в качестве потока платежей и поступлений рассматривать последовательность a(0), a(1), a(2), a(3), ... , a(t), .... Если величина a(k) отрицательна, то это платеж, а если она положительна - поступление. Выше был рассмотрен важный частный случай - поток с одним платежом a(0) = (-А) и дальнейшими поступлениями a(1) = a(2) = a(3) = ... = a(t) = .... = В.

Чистую текущую стоимость, или, как ее иногда называют, дисконтированную прибыль, чистый приведенный доход (или эффект, или величину, по-английски - Net Present Value, сокращенно NPV), т.е. разность между дисконтированными доходами и расходами, рассчитывают для потока платежей путем приведения затрат и поступлений к одному моменту времени:

NPV = a(0) + a(1)С(1) + a(2)С(2) + a(3)С(3) + ... + a(t)С(t) + ... (4),

где С(t) - дисконт-функция, определяемая по формулам (2) или (3). В простейшем случае, когда дисконт-фактор не меняется год от года и согласно формуле (1) имеет вид С = 1 / (1+ q), где q - банковский процент, формула для чистой текущей стоимости конкретизируется:

NPV = NPV(q) = a(0) + a(1)/ (1+ q) + a(2)/ (1+ q)2+ a(3)/ (1+ q)3+ ...

+ a(t)/ (1+ q)t+ ....(5)

Пусть, например, a(0) = - 10, a(1) = 3, a(2) = 4, a(3) = 5. Пусть q = 0,12, тогда, как установлено выше, согласно формуле (2) значения дисконт-функции таковы: С(1) = 0,89, С(2) = 0.80, а С(3) = 0,71. Тогда согласно формуле (4)

NPV(0,12) = - 10 + 3 х 0,89 + 4 х 0.80 + 5 х 0,71 =

= - 10 + 2,67 + 3,20 + 3,55 = - 0,58.

Таким образом, этот проект является невыгодным для вложения капитала, поскольку NPV(0,12) отрицательно, в то время как при отсутствии дисконтирования (т.е. при С = 1, q = 0) вывод иной: NPV(0) = - 10 + 3 + 4 + 5 = 2.

Таким образом, важной проблемой является выбор дисконт-функции. В качестве приближения обычно используют постоянное дисконтирование, хотя экономическая история последних лет показывает, что банки часто меняют проценты платы за депозит, так что формула (3) для дисконт-функции с различными процентами в разные годы более реалистична, чем формула (2).

Часто предлагают использовать норму дисконта, равную приемлемой для инвестора норме дохода на капитал. Это предложение означает, что экономисты явным образом обращаются к инвестору как к эксперту, который должен назвать им некоторое число исходя из своего опыта и интуиции. Кроме того, при этом игнорируется изменение указанной нормы во времени.

При использовании чистой текущей стоимости значение экономического эффекта во многом определяется выбранным для расчета нормативом (коэффициентом) дисконтирования - показателя, используемого для приведения по фактору времени ожидаемых денежных поступлений и платежей. Выбор численного значения этого показателя зависит от таких факторов, как:

· цели инвестирования и условия реализации проекта;

· уровень инфляции в конкретной национальной экономике;

· величина инвестиционного риска;

· альтернативные возможности вложения капитала;

· финансовые и иные соображения и представления инвестора.

Считается, что для различных классов инвестиций могут выбираться различные значения коэффициента дисконтирования. В частности, вложения, связанные с защитой рыночных позиций предприятия, оцениваются по весьма низкому нормативу 6%.

Инвестициям в обновление основных фондов соответствует норматив дисконтирования 12%, а вложениям с целью экономии текущих затрат - 15%. Для вложений, нацеленным на увеличение доходов предприятия, используют коэффициент дисконтирования 20%, а для рисковых капиталовложений - 25%.

В литературе подчеркивается зависимость коэффициента дисконтирования от степени риска проекта. Для обычных проектов приемлемой считается ставка 16%, для новых проектов на стабильном рынке - 20%, для проектов, базирующихся на новых технологиях, - 24%.

Хотя в конечном счете выбор значения дисконта, который играет роль порогового (минимального) значения норматива рентабельности капиталовложений, является прерогативой инвестора, в практике проведения инвестиционных расчетов часто в качестве ориентира используют ставку процента государственных ценных бумаг. Считается, что при этой ставке государство гарантирует хозяйствующим субъектам возврат инвестируемого капитала без какого-либо риска. В российской практике ориентиром является также ставка рефинансирования Центрального банка, определяющая нижнюю границу платы за кредит.

Индекс рентабельности инвестиций. Этот критерий является по сути вариантом предыду­щего. Индекс рентабельности (РI) рассчитывается по формуле:

n P_k

PI = å ¾¾¾ : IC .

^k=1 (1+q)^k

Очевидно, что если:

РI > 1, то проект следует при­нять,

РI < 1, то проект следует от­вергнуть,

РI = 1, то проект не является ни прибыльным, ни убыточ­ным.

В отличие от чистой текущей стоимости индекс рентабельности является относительным показателем: он характеризует уровень доходов на единицу затрат, т.е. эффективность вложений — чем больше значение этого показателя, тем выше отдача каждого рубля, инвестированного в данный проект. Благодаря этому критерий РI очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинако­вые значения NPV, в частности, если два проекта име­ют одинаковые значения NPV, но разные объемы тре­буемых инвестиций, то очевидно, что выгоднее тот из них, который обеспечивает большую эффективность вложений.

В отличие от (валовой) прибыли, рентабельность - это частное от деления прибыли на расходы (инвестиции). Обозначим доходы как Д, расходы как Р, тогда прибыль П = Д - Р, а рентабельность Ре = Д / Р - 1. Другими словами, рентабельность - это относительная прибыль, она показывает, какой доход приносит 1 руб. вложений.

Прибыль и рентабельность - два принципиально разных критерия. Максимизация по ним весьма часто приводит к разным результатам. В отличие от прибыли рентабельность выше для небольших проектов, как правило, использующих побочные результаты реализации крупных проектов. Например, организация розничной торговли среди строителей ГЭС опирается на использование дорог и наличие потребительского спроса. И то, и другое - результаты реализации проекта строительства ГЭС. При этом рентабельность торгового проекта, очевидно, во много раз выше рентабельности строительства ГЭС, что, например, должно учитываться при налогообложении.

Под внутренней нормой доходности инвестиций (обозначается IRR,, синонимы: внутренняя норма прибыли, внутренняя норма окупа­емости) понимают значение коэффициента дисконти­рования q, при котором NPV проекта равна нулю:

IRR = q, при котором NPV(q) = 0.

Иными словами, если обозначить IС = CF₀ и CF_k – элемент финансового потока проекта, соответствующий k-му моменту времени, то IRR находится из уравнения:

_n CF_k

å ¾¾¾¾ = 0 .

^k=0 (1+IRR)^k

Смысл расчета внутренней нормы прибыли при ана­лизе эффективности планируемых инвестиций, как правило, заключается в следующем: IRR показывает верхнюю границу зоны ожи­даемой доходности проекта, и, следовательно, макси­мально допустимый относительный уровень расходов. Например, если проект полностью финансиру­ется за счёт ссуды коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любая организация фи­нансирует свою деятельность, в том числе и инвес­тиционную, из различных источников. В качестве пла­ты за пользование авансированными в деятельность организации финансовыми ресурсами она уплачива­ет проценты, дивиденды, вознаграждения и т.п., ины­ми словами, несет некоторые обоснованные расхо­ды на поддержание экономического потенциала. По­казатель, характеризующий относительный уровень этих расходов в отношении долгосрочных источни­ков средств, называется средневзвешенной ценой капитала (WACC). Этот по­казатель отражает сложившийся в организации минимум возврата на вложенный в ее деятельность капитал, его рентабельность, и рассчи­тывается по формуле средней арифметической взве­шенной.

Таким образом, экономический смысл критерия IRR заключается в следующем: организации выгодно принимать любые решения инвестиционного характера, внутренние нормы доходности которых не больше текущего значения показателя "цена капитала" СС. Под показателем СС понимается либо WACC, если источник средств точно не идентифицирован, либо цена целе­вого источника, если таковой имеется. Именно с пока­зателем СС сравнивается критерий IRR, рассчитанный для конкретного проекта, при этом связь между ними такова.

Если:

IRR < СС, то проект следует принять;

IRR > СС, то проект следует отвергнуть;

IRR = СС, то проект не является ни прибыль­ным, ни убыточным.

Независимо от того, с чем сравнивается IRR, оче­видно одно: проект принимается, если его IRR меньше некоторой пороговой величины; поэтому при прочих равных условиях, как правило, меньшее значение IRR считается предпочтительным.

Итак, неопределенности, связанной с произволом в выборе нормы дисконта инвестором, можно избежать, рассчитав так называемую. внутреннюю норму доходности (или прибыли, по-английски Internal Rate of Return, сокращенно IRR), т.е. то значение дисконт-фактора, при котором чистая текущая стоимость оказывается равной 0. Ожидается, что при меньшем значении дисконт-фактора прибыль положительна, а при большем - отрицательна. К сожалению, такая интерпретация не всегда допустима, поскольку для некоторой совокупности потоков платежей чистая текущая стоимость равна 0 не для одного значения дисконт-фактора, а для многих (см. об этом, например, монографии [3,4]). Однако традиционная интерпретация корректна в подавляющем большинстве реальных ситуаций, в частности, если платежи всегда предшествуют поступлениям. Поэтому многие экономисты считают наиболее целесообразным использование внутренней нормы доходности как основной характеристики при сравнении потоков платежей.

Внутреннюю норму доходности для рентабельности можно было бы определить из условия равенства 0 рентабельности как функции от нормы дисконта. Однако это условие означает, что доходы и расходы равны, т.е. прибыль равна 0. Поэтому внутренние нормы доходности для прибыли и рентабельности совпадают.

Срок окупаемости инвестиций. Этот критерий, являющийся одним из самых простых и широко распространенных в мировой учетно-аналитичес­кой практике, не предполагает учета временной упорядоченно­сти денежных поступлений. Алгоритм расчета срока оку­паемости (РР) зависит от равномерности распределения прогнозируемых доходов от инвестиций. Если доход распределен по годам равномерно, то срок окупаемости рассчитывается делением единовременных затрат на величину годового дохода, обусловленного ими. При получении дробного числа оно обычно округляется в сторону увеличения до ближайшего целого. Если прибыль рас­пределена неравномерно, то срок окупаемости рассчи­тывается прямым подсчетом числа лет, в течение кото­рых инвестиция будет погашена кумулятивным доходом. Общая формула расчета показателя РР имеет вид:

_n

РР = min n, при котором å P_k ³ IC.

^k=0

Нередко показатель РР рассчитывается более точ­но, т.е. рассматривается и дробная часть года; при этом делается предположение, что де­нежные потоки распределены равномерно в течение каждого года.

Некоторые специалисты при расчете показателя РР все же рекомендуют учитывать временной аспект. В этом случае в расчет принимаются денежные потоки, дисконтированные по показателю WACC, а соответ­ствующая формула для расчета дисконтированного срока окупаемости, DPP, имеет вид:

_n 1

DPP = min n, при котором å P_k • ¾¾¾ ³ IC.

^k=1 (1+q)^k

Очевидно, что в случае дисконтирования срок окупаемости увеличива­ется, т.е. всегда DPP > РР. Иными словами, проект, приемлемый по критерию РР, может оказаться непри­емлемым по критерию DPP. Очевидно, что показатель РР соответствует случаю, когда q=0.

Итак, срок окупаемости - тот срок, за который доходы покроют расходы. Предполагается, что после этого проект (инвестиционный проект, или проект изменения налоговой системы, в частности, ставок налогов, или же какой-либо иной) приносит только прибыль. Очевидно, это верно не для всех проектов. Потому понятие "срок окупаемости" применяют прежде всего к тем проектам, в которых за единовременным вложением средств следует ежегодное получение прибыли.

Простейший (и наименее обоснованный) способ расчета срока окупаемости состоит в делении объема вложений А на ожидаемый ежегодный доход В. Тогда срок окупаемости РР равен А/В. Пусть, например, А - это разовое уменьшение налоговых сборов в результате снижения ставок, а В - ожидаемый ежегодный прирост поступлений в бюджет, обеспеченный расширением налоговой базы в результате ускоренного развития производства.

Этот способ не учитывает дисконтирование. К чему приведет введение в расчет дисконт-фактора? Пусть, как и ранее, объем единовременных вложений равен А, причем начиная с конца первого года проект дает доход В ежегодно (точнее, доход поступает порциями, равными В, с момента, наступающего через год после вложения, и далее с интервалом в год). Если дисконт-фактор равен С, то максимально возможный суммарный доход равен

ВС + ВС2+ ВС3+ ВС4+ ВС5+ ... = ВС ( 1 + С + С2 + С3 + С4 + ... )

В скобках стоит сумма бесконечной геометрической прогрессии, равная, как известно, величине 1/(1-С). Следовательно, максимально возможный суммарный доход от первого года после вложения до скончания мира равен ВС/(1-С).

Отсюда следует, что если А/В меньше С/(1-С), то можно указать (рассчитать) срок окупаемости проекта, но он будет больше, иногда существенно больше, чем А/В. Если же А/В больше или равно С/(1-С), то проект не окупится никогда. Поскольку максимально возможное значение С равно 0,89, то проект не окупится никогда, если А/В не меньше 0,89/ 0,11 = 8,09.

Пусть вложения равны 1 миллиону рублей, ежегодная прибыль составляет 500 тысяч, т.е. А/В = 2. Пусть дисконт-фактор С = 0.8. Каков срок окупаемости? При примитивном подходе (соответствующем С = 1) он равен 2 годам. А на самом деле?

За k лет будет возвращено

ВС ( 1 + С + С2 + С3 + С4 + ...+ Сk)= ВС ( 1 - Сk+1) / (1-С) ,

согласно известной формуле для суммы конечной геометрической прогрессии. Для срока окупаемости получаем уравнение

1 =0,5 х 0,8 (1 - 0,8 k+1) / (1- 0,8), (6)

откуда 0,5 = (1 - 0,8 k+1), или 0,8 k+1 = 0,5. Прологарифмируем обе части последнего уравнения: (k+1) ln 0,8 = ln 0,5 , откуда

(k+1) = ln 0,5 / ln 0,8 = (- 0,693) / (- 0,223) = 3,11, k = 2,11.

Срок окупаемости оказался в данном примере равном 2,11 лет, т.е. увеличился примерно на 4 недели. Это немного. Однако если В = 0,2, то вместо (6) мы имели бы

1 =0,2 х 0,8 ( 1 - 0,8 k+1) / (1- 0,8),

Это уравнение не имеет решения, поскольку А / В = 5 > С/(1-С) = 0.8 / (1- 0,8) =4, проект не окупится никогда. Окупаемости можно ожидать лишь в случае А/В < 4. Рассмотрим и промежуточный случай, В = 0,33, с "примитивным" сроком окупаемости 3 года. Тогда вместо (6) имеем уравнение

1 =0,33 х 0,8 (1 - 0,8 k+1) / (1- 0,8), (7)

откуда 0,76 = (1 - 0,8 k+1), или 0,8 k+1 = 0,24. Прологарифмируем обе части последнего уравнения: (k+1) ln 0,8 = ln 0,24 , откуда

(k+1) = ln 0,24 / ln 0,8 = (- 1.427) / ( - 0,223) = 6,40, k = 5,40.

Итак, реальный срок окупаемости - не три года, а согласно уравнению (7) чуть менее пяти с половиной лет.

Если вложения делаются не единовременно или доходы поступают по иной схеме, то расчеты усложняются, но суть дела остается той же.

Таким образом, срок окупаемости зависит от неизвестного дисконт-фактора С или даже от неизвестной дисконт-функции - ибо какие у нас основания считать будущую дисконт-функцию постоянной? Иногда (в том числе в официальных изданиях [8]) рекомендуется использовать норму дисконта (дисконт-фактор), соответствующую ПРИЕМЛЕМОЙ для инвестора норме дохода на капитал. Мы не знаем, какую норму дисконта тот или иной инвестор сочтет приемлемой. Однако ясно, что она зависит от ситуации в экономике в целом. То, что представляется выгодным сегодня, может оказаться невыгодным завтра, или наоборот. Тем самым решение перекладывается на инвестора, который фактически выступает в роли эксперта по выбору нормы дисконта.

Коэффициент эффективности инвестиций. Этот критерий имеет две характерные черты: во-пер­вых, он не предполагает дисконтирования показателей дохода; во-вторых, доход характеризуется показателем чистой прибыли PN (прибыль за минусом отчислений в бюджет). Алгоритм расчета исключительно прост, что и предопределяет широкое использование этого пока­зателя на практике. Коэффициент эффективности инвестиции, называемый также учетной нормой при­были (ARR), рассчитывается делением среднегодовой прибыли PN на среднюю величину инвестиций (коэф­фициент берется в процентах). Средняя величина инвестиций находится делением исходной суммы ка­питальных вложений на два, если предполагается, что по истечении срока реализации анализируемого про­екта все капитальные затраты будут списаны. Если допускается наличие остаточной или ликвидационной стоимости (RV), то ее оценка должна быть учтена в расчетах. Иными словами, существуют различные алгоритмы исчисления показателя ARR. Достаточно распространенным является следующий:

PN

ARR = ¾¾¾¾¾ .

1/2•(IC+RV)

Данный показатель чаще всего сравнивается с ко­эффициентом рентабельности авансированного капи­тала, рассчитываемого делением общей чистой при­были организации на общую сумму средств, авансированных в ее деятельность (итог сред­него баланса-нетто).

Метод, основанный на коэффициенте эффективно­сти инвестиции, также имеет ряд существенных недо­статков, обусловленных в основном тем, что он не учитывает временной компоненты денежных потоков. В частности, метод не делает различия между проек­тами с одинаковой суммой среднегодовой прибыли, но варьирующей суммой прибыли по годам, а также меж­ду проектами, имеющими одинаковую среднегодовую прибыль, но генерируемую в течение различного ко­личества лет, и т.п.

Критерии (показатели, характеристики финансовых потоков) используются для оценки и сравнения инвестиционных проектов, выбора из них наиболее предпочтительных для инвестора. Поскольку рассмотренные показатели (критерии, характеристики финансовых потоков) относятся к различным моментам времени, ключевой проблемой здесь является их сопоставимость между собой. Относиться к результатам сопоставления тех или иных критериев можно по-разному в зависимости от существующих объективных и субъективных условий: темпа инфляции, размера инвестиций и генерируемых поступлений, горизонта прогнозирования, уровня квалификации аналитика и т.п.

Пример оценки инвестиционного проекта.Пусть предприятие реализует инвестиционный проект, требующий 200 млн. рублей капитальных вложений. Освоение инвестиций происходит в течение 3 лет. В первый год осваивается 25% инвестиций, во второй – 30% инвестиций, в третий – 45%.

Доля кредита в инвестициях составляет 30%. Выдача кредитных сумм производится равномерно. Плата за предоставленный кредит составляет 15% годовых (начисляемых по формуле простых процентов). Кредит предоставляется на 3,5 года.

Срок реализации проекта составляет 5 лет, а срок службы созданных мощностей – 8 лет. Амортизация начисляется по линейной схеме. Ликвидационная стоимость оборудования составляет 10% от первоначальной. Прогнозируемая продажная стоимость ликвидируемого имущества выше остаточной стоимости на 10%.

Цена единицы продукции 120 тыс. руб. Переменные издержки составляют 50 тыс.руб./ед. Постоянные издержки составляют 50 миллионов рублей в год. Размер оборотного капитала - 10% от выручки.

Прогнозируемый коэффициент дисконтирования при расчетах NPV составляет 10%. Темп инфляции оценивается как 6% (+1%).

Оптимистическая оценка инвестиционного проекта превышает среднюю оценку на 1,06%, а пессимистическая оценка хуже средней на 1,05%. Вероятность пессимистичного исхода равна 0,09, а вероятность оптимистического 0,07.

Перечисленные показатели являются исходными для определения экономической эффективности инвестиционного проекта в целом, причем в качестве базовых для инвестиционных расчетов выступают прогнозные величины поступлений и платежей денежных средств в течение всего инвестиционного периода. Для удобства анализа эти величины могут быть представлены в табличной форме или в форме графика, отражающего моменты и объемы финансовых поступлений и платежей в течение всего инвестиционного периода.

Требуется определить:

· приемлемость проекта по критерию NPV.

· его чувствительность к изменению объемов сбыта, уровня цен, переменных и постоянных издержек, ставки за кредит.

· среднюю рентабельность инвестиций, срок возврата инвестиций, внутреннюю норму прибыли.

Могут представлять интерес также иные характеристики проекта.

Приемлемость проекта по критерию NPV.Чистая текущая стоимость проекта NPV является важнейшим критерием, по которому судят о целесообразности инвестирования в данный проект. Для определения NPV необходимо спрогнозировать величину финансовых потоков в каждый год реализации проекта, а затем привести их к общему знаменателю для возможности сравнения во времени. В рассматриваемом случае номинальная ставка дисконтирования равна r_n = 10%, тогда, учитывая темп инфляции i = 6% в год, реальная (т.е. чистая, освобожденная от влияния инфляции) ставка дисконтирования составляет 3,77%:

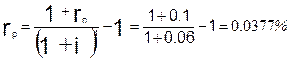
В начальном варианте расчета объем производства составляет 2000 единиц продукции в год. Как показывают расчеты, NPV такого проекта равен 372,4 млн. руб., что означает его приемлемость по данному критерию. Поскольку NPV>0, то при данной ставке дисконтирования проект является выгодным для предприятия.

Чувствительность NPV проекта к изменению объемов сбыта, уровня цен, переменных и постоянных издержек. Необходимо определить наиболее существенные параметры проекта и степень их влияния на NPV при изменении этих параметров в неблагоприятную сторону. Таким образом, анализ чувствительности позволяет оценить рискованность проекта и потери в случае реализации пессимистического прогноза. Для данного проекта был принят следующий пессимистический вариант:

^· объем производства снижается на 5% ;

^· цена снижается на 5% ;

^· постоянные затраты повышаются на 5% ;

^· переменные затраты повышаются на 5%.

Расчеты показывают, что уменьшение объема производства на 5% приводит к снижению NPV до величины 342,8 млн. руб., что на 7,96% меньше базовой. Уменьшение цены за единицу продукции на 5% приводит к снижению NPV до величины 321,3 млн. руб., что на 13,73% меньше базовой. Увеличение постоянных затрат на 5% приводит к снижению NPV до величины 366,3 млн. руб., что на 1,63% меньше базовой. Увеличение переменных затрат на 5% приводит к снижению NPV до величины 350,9 млн. руб., что на 5,77% меньше базовой. Итак, наибольшее влияние на NPV оказываютцена и объем производства.

Оценка целесообразности осуществления проекта. Прежде чем принимать окончательное решение о целесообразности осуществления данного проекта, необходимо оценить риск, связанный с его реализацией. Для данного проекта имеем: при наиболее вероятном исходе NPV_{ожидаемый}=372,4 млн. руб. при оптимистичном исходе NPV_{оптимистичный} = 394,7 млн. руб., при пессимистическом исходе NPV_{писсимис} = 353,8 млн. руб., а средневзвешенное значение (т.е. математическое ожидание) есть 372, 3 млн. руб.

Для данного проекта (недисконтированная) рентабельность инвестиций равна 167%. Срок окупаемости (возврата инвестиций) показывает, через сколько лет будут возвращены первоначально затраченные средства. Для данного проекта из рис.2 видно, что возврат инвестиций происходит в начале пятого года.

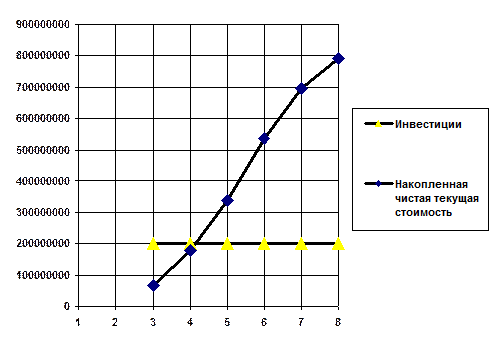
Рис.2. Накопленная чистая текущая стоимость и срок окупаемости.

Для определения внутренней нормы прибыли (ВНП) проекта нужно приравнять NPV к нулю. На основе вычислений, представленных на рис.3, заключаем, что ВНП данного проекта равна 14%. Это выше нормы дисконтирования, что означает приемлемость данного варианта проекта по этому критерию.

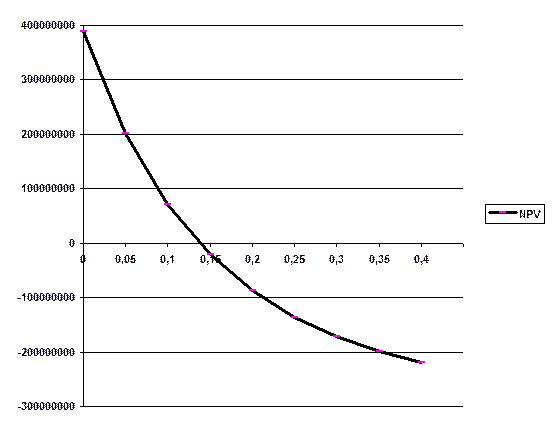
Рис.3. Нахождение внутренней нормы доходности.

Подведем итоги. В ходе оценки данного инвестиционного проекта было проверено его соответствие различным критериям приемлемости, а также произведен анализ его основных параметров и вариантов. В результате можно сделать следующие выводы:

1. Базовый вариант проекта является приемлемым по критерию NPV и по критерию внутренней нормы рентабельности.

2. Анализ чувствительности NPV показывает близость таких параметров проекта, как цена за единицу продукции и переменные издержки, к их пороговым значениям, за которыми проект будет убыточным. Это делает проект рискованным.

3. Сопоставление результатов, получаемых различными методами, дает возможность скорректировать границы зоны неопределенности значения прогнозируемого показателя и отдельные управляемые параметры системы. А также обосновать с учетом привлечения дополнительных экспертных оценок выбор наиболее вероятного варианта реализации показателя в прогнозном периоде.

1.5.6. Оценки погрешностей характеристик финансовых потоков инвестиционных проектов и проблема горизонта планирования

Погрешности экономических измерений. Все знают, что любое инженерное измерение проводится с некоторой погрешностью. Эту погрешность обычно приводят в документации (техническом паспорте средства измерения) и учитывают при принятии решений. Ясно, что и любое экономическое измерение также проводится с погрешностью. А вот какова она? Необходимо уметь ее оценивать, поскольку ошибки при принятии экономических решений обходятся дорого.

Например, чистая текущая стоимость, срок окупаемости и сам вывод о прибыльности проекта зависят от неизвестного дисконт-фактора С или даже от неизвестной дисконт-функции - ибо какие у нас основания считать будущую дисконт-функцию постоянной? Экономическая история России последних лет показывает, что банки часто меняют проценты плат за депозит и за кредит. Как известно, часто предлагают использовать норму дисконта, равную приемлемой для инвестора норме дохода на капитал. Это значит, что экономисты явным образом обращаются к инвестору как к эксперту, который должен назвать им некоторое число исходя из своего опыта и интуиции (т.е. экономисты перекладывают свою работу на инвестора). Кроме того, при этом игнорируется изменение указанной нормы во времени.

Количественная оценка компонентов инвестиций, в частности, денежных поступлений и платежей, представляет собой сложную задачу, поскольку на каждый из них оказывает влияние множество разнообразных факторов, а сами оценки охватывают достаточно длительный промежуток времени. В частности, для рассматриваемого примера важно учитывать следующие характеристики инвестиционного проекта:

· возможные колебания рыночного спроса на продукцию;

· ожидаемые колебания цен на потребляемые ресурсы и производимую продукцию;

· возможное появление на рынке товаров-конкурентов;

· планируемое снижение производственно-сбытовых издержек по мере освоения новой продукции и наращивания объемов производства;

· влияние инфляции на покупательную способность потребителей и, соответственно, на объемы продаж.

Поэтому такие оценки базируются на прогнозах внутренней и внешней среды предприятия. Использование прогнозных оценок всегда связано с риском, возрастающим при увеличении масштаба проекта и длительности инвестиционного периода.

Оценка компонентов инвестиций связана также с анализом источников финансирования. Причем для целей проводимого анализа особое внимание уделяется внешним источникам, в частности, акционерному капиталу и планируемым затратам по обслуживанию привлеченного капитала: размерам дивидендов, периодичности их выплат и т.п.

Оценка погрешности NPV. В качестве примера рассмотрим исследование чистой текущей стоимости NPV на устойчивость (чувствительность) к малым отклонениям значений дисконт-функции. Для этого надо найти максимально возможное отклонение NPV при допустимых отклонениях значений дисконт-функции (или, если угодно, значений банковских процентов). В качестве примера рассмотрим инвестиционный проект, описываемый финансовым потоком из четырех элементов:

NPV = NPV (a(0), a(1), С(1), a(2), С(2), a(3), С(3))=

= a(0) + a(1)С(1) + a(2)С(2) + a(3)С(3).

Предположим, что изучается устойчивость (чувствительность) для ранее рассмотренных значений

a(0)=-10, a(1)=3, a(2)=4, a(3)=5, С(1)=0,89, С(2)=0,80, С(3)=0,71.

Пусть максимально возможные отклонения С(1), С(2), С(3) равны +0,05. Тогда максимум значений NPV равен

NPVmax= -10+3х0,94+4х0.85+5х0,76 = -10+ 2,82 + 3,40 + 3,80 = 0,02,

в то время как минимум значений NPV есть

NPVmin= -10+3х0,84+4х0.75+5х0,66 = -10 +2,52 +3,00+3,30 = -1,18.

Для NPV получаем интервал от (-1,18) до (+0,02). Его длина достаточно велика. В нем есть и положительные, и отрицательные значения. Так что не удается сделать однозначного заключения - будет проект убыточным или выгодным. Для принятия решения не обойтись без экспертов.

Есть много подходов к изучению чувствительности экономических величин и основанных на них выводах, которые нет возможности рассмотреть здесь (см. монографию [5]). Обратите, например, внимание на то, что величины a(0), a(1), a(2), a(3) в только что рассмотренном примере изучения чувствительности считались постоянными. А ведь это - упрощение ситуации, трудно предсказать на три года вперед возможность выполнения обязательств.

Что с точки зрения экономической теории означает приравнивание дисконт-функции константе? В монографии [5] показано, что необходимым и доста