Эквивалентность процентных ставок и финансовая эквивалентность платежей.

Простые ставки процентов

Практически все финансово – экономические расчеты связаны с определением процентных денег. Процентными деньгами (процентами) называют сумму доходов от предоставления денег в долг в любой форме (выдача ссуд, открытие депозитных счетов, покупка облигаций, сдача оборудования в аренду и т.п.) Сумма процентных денег зависит от суммы долга, срока его выплаты и процентной ставки, характеризующей интенсивность начисления процентов. Сумму долга с начисленными процентами называют наращенной суммой. Отношение наращенной суммы к первоначальной сумме долга называют множителем (коэффициентом) наращения. Интервал времени, за который начисляют проценты, называют периодом начисления.

При использовании простых ставок процентов сумма процентных денег определяется исходя из первоначальной суммы долга независимо от количества периодов начисления и их длительности по формуле:

I = n · i · P, где

n – срок долга в годах;

i – годовая ставка простых процентов в относительных единицах;

P – первоначальная сумма долга.

Наращенная сумма на каждом периоде начисления будет определяться формулой:

S = P · ( 1 + n · i ) = P · k_нп , где

k_нп– коэффициент наращения.

Приведенная формула используется как для определения суммы вклада с процентами, так и для определения суммы кредита с процентами при его погашении единовременным платежом.

Пример 1.Банк принимает вклады до востребования по простой ставке 8% годовых. Определить сумму процентов на вклад 2000 руб., размещенный на полгода.

Решение

Сумма вклада с процентами:

S = 2000 · ( 1+0,5 · 1,08 ) = 2080 руб.

Сумма начисленных процентов:

I = S – P = 2080 – 2000 = 80 руб.

Сумму начисленных процентов можно также определить по формуле:

I = n ∙ i ∙ P = 0.5 ∙ 0,08 ∙ 2000 = 80 руб.

Если срок долга задается в днях, в приведенную формулу надо подставить выражение:

n= 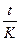, где

t - продолжительность периода начисления в днях;

K- Расчетное количество дней в году (временная база).

Наращенная сумма при этом будет определяться по формуле:

S = P ∙ ( 1 + 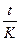∙ i )

Количество дней в году может браться точно – 365 или 366 дней (точные проценты) или приближенно – 360 дней (обыкновенные проценты). Количество дней в каждом целом месяце в течение срока долга также может браться точно или приближено (30 дней). В мировой банковской практике использование приближенного количества дней в каждом целом месяце и обыкновенных процентов называется “ германской практикой ”, точного числа дней в каждом месяце и обыкновенных процентов – “ французской практикой ”, точного числа дней в каждом месяце и точных процентов – “ английской практикой ”. В зависимости от использования конкретной практики начисления процентов их сумма будет различаться.

Пример 2.Вклад 2000 руб. был положен в банк 12 марта 2004 г. и востребован 25 декабря того же года. Ставка процентов составляла 8 % годовых. Определить сумму начисленных процентов при различной практике их начисления.

Решение

1. При германской практике расчетное количество дней для начисления процентов равно: [ 20 (март) + 30 (апрель) +30 (май) + 30 (июнь) + 30 (июль) + 30 (август) + 30 (сентябрь) + 30 (октябрь) + 30 (ноябрь) + 25 (декабрь) – 1 (день выдачи денег в долг и день их возвращения считаются за один день) ] = 284 дня

Ссумма начисленных процентов составит:

I = 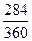∙ 0,08 ∙ 2000 = 126,2 руб.

2. При французской практике расчетное количество дней для начисления процентов равно: [20+30+31+30+31+31+30+31+30+25-1]=288 дней.

Сумма начисленных процентов будет равна:

I = 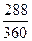∙ 0,08 ∙ 2000 = 128,0 руб.

3. При английской практике сумма начисленных процентов составит:

I = 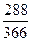∙ 0,08 ∙ 2000 = 125,9 руб.

Для расчета процентов может быть использована методика расчета с вычислением процентных чисел. При этом каждый раз, когда сумма на счете изменяется, производится расчет процентного числа за прошедший период, в течение которого сумма на счете оставалась неизменной, по выражению:

Процентное число = Сумма х Длительность периода в днях

Для определения суммы процентов за срок их начисления все процентные числа складываются, и их сумма делится на постоянный делитель, равный:

Постоянный делитель = Количество дней в году

Годовая ставка процентов

Обратите внимание, что готовая ставка процентов при этом берется по своей абсолютной величине.

Пример 3. При открытии сберегательного счета по ставке 12% годовых 20 мая 2004 г. на счет была положена сумма 10 тыс. руб. Затем 5 июля на счет была добавлена сумма 5 тыс. руб., 10 сентября со счета бала снята сумма 7.5 тыс. руб., а 20 ноября счет был закрыт. Используя процентные числа, определить сумму начисленных процентов.

Решение

Будем считать, что начисление процентов проводилось по германской практике. В этом случае срок хранения суммы 10 тыс. руб. составил 46 дней, суммы 15 тыс. руб. – 66 дней, суммы 7.5 тыс. руб. – 70 дней.

Сумма процентных чисел будет равна:

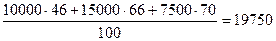
Постоянный делитель равен:

360 : 12 = 30

Следовательно, сумма начисленных процентов будет равна:

19750 : 30 = 658,3 руб.

Обратите внимание, что такая методика по своей сути является последовательным применением формулы процентных денег на каждом интервале постоянства суммы на счете. В рассматриваемом случае:

I = I₁ + I₂ + I3 = 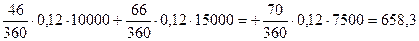руб

Если ставка процентов в течение срока долга будет изменяться, наращенная сумма будет равна:

S = P ∙ (1 + n₁i₁ + n₂i₂ +...+ n_Ni_N) , где

N – количество периодов начисления ;

n_t ( t = 1 , 2 ... , N ) – длительность t -го периода начисления;

i_t ( t = 1 , 2, ... , N ) – простая ставка процентов на t-м периоде начисления.

Пример 4.Вклад 20 тыс. руб. был положен в банк 25 мая 2004 г. по ставке 9% годовых. С 1 июля банк снизил ставку по вкладам до 3 % годовых, 15 июля вклад был востребован. Определить сумму начисленных процентов при английской практике их начисления.

Решение

Количество дней для начисления процентов по ставке 9 % годовых равно 37, по ставке 3% годовых – 14 дням.

Сумма начисленных процентов будет равна:

I = 20000 · 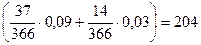руб.

Используя формулу для наращенной суммы можно определить:

а) срок долга

в годах

n =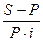

или в днях

t =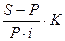

б) ставку процентов

i =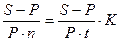

в) первоначальную сумму долга

P =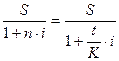

Последняя операция называется дисконтированием по простой ставке процентов. Термин «дисконтирование» в широком смысле означает определение значения стоимостной величины на некоторый момент времени, если задано ее значение в будущем. Дисконтирование позволяет учитывать в стоимостных расчетах фактор времени.

При проведении процентных расчетов может быть учтена инфляция – снижение покупательной способности денег. Инфляцию за некоторый период времени характеризуют ее уровнем, показывающим, во сколько раз выросли цены.

Уровень инфляции и индекс инфляции за один и тот же период связаны соотношениями:

H = ( Ip –1) 100

I_p =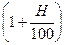

где Ip – индекс инфляции;(в коэффициентах)

H – уровень (темп) и инфляция (в %)

Если задан уровень инфляции за некоторый период (например, месяц), то индекс инфляции за срок, включающий несколько таких периодов (например, квартал, полугодие, год) определяется по формуле:

I = 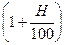^N

H – уровень инфляции за период;

N – количество таких периодов в течение рассматриваемого срока.

Пример 5.Определить ожидаемый годовой уровень инфляции при месячном уровне инфляции 1.6 и 1.2 %.

Решение

При месячном уровне инфляции 1.6 % индекс инфляции за год составит:

Ip = (1 + 0,016)12 = 1,21

Следовательно, ожидаемый годовой уровень инфляции будет равен:

H = (1,21 - 1)·100=21%

При месячном уровне инфляции 1.2 % индекс инфляции за год составит.

Ip = (1+0,012)12 =1,154

Годовой уровень инфляции будет равен:

H = (1,154-1)·100 =15,4 %

Инфляция будет влиять на реальную (с точки зрения покупательной способности) доходность вкладных и кредитных операций. Реальное значение суммы с начисленными процентами за некоторый срок, пересчитанное (приведенное) к моменту предоставления денег в долг, будет равно:

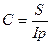
Где Ip - индекс инфляции за срок долга.

C - Наращенная сумма с учетом ее обесценения

При использовании простых ставок процентов и одном периоде их начисления:

C =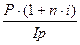

Пример 6.Банк принимает депозиты на полгода по ставке 9 % годовых. Определить реальные результаты вкладной операции для размера вклада 50 тыс. руб. при месячном уровне инфляции 1.8 %

Решение

Сумма влада с процентами будет равна:

S = 500008·( 1+ 0,5·0,09)=52250 руб.

Индекс инфляции за срок хранения депозита составит:

Ip = (1 + 0,018)⁶ = 1,113

Следовательно сумма вклада сначисленными процентами по своей покупательной способности с учетом инфляции будет соответствовать, сумме:

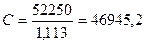руб.

При выдаче кредитов уровень инфляции может быть учтен при определении ставки процентов по кредиту (брутто-ставки r). Общая формула для определения простой ставки процентов по кредиту, компенсирующей ожидаемую инфляцию, при одном периоде начисления имеет вид:

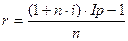
где r - брутто-ставка;

Простые учетные ставки

Учетные ставки обычно используются при определении процентных денег при покупке (учете) банком векселей или других денежных обязательств. При этом банк до наступления платежа по векселю покупает его у предъявителя по цене, меньшей суммы, которая должна быть выплачена по нему в момент его погашения. Доход банка от такой операции, равный разности между суммой по векселю и ценой его покупки, называется дисконтом, Сумма процентных денег (дисконт) при этом определяется исходя из суммы по векселю, и равна

где n- срок в долях года от даты учета до даты погашения векселя;

d – годовая учетная ставка в относительных единицах;

S – сумма по векселю;

t – количество дней от даты учета до даты погашения векселя.

Сумма, полученная предъявителем векселя, будет равна:

P = S - D = S · (1 ­ n · d) = S · (1­

Пример 8. Вексель на сумму 50 тыс. руб. предъявлен в банк за погода до срока его погашения. Банк для определения своего дохода использует учетную ставку, равную 2% годовых. Определить сумму, выплаченную предъявителю векселя, и суму дохода, полученного банком.

Решение

Сумма, полученная предъявителем векселя, будет равна:

P=50000·(1­1,5·0,02)=4950 руб.

Сумма дисконта, полученного банком, составит:

D=50000-49500=500 руб.

Или

D= 0,5·0,02·50000=500 руб.

Аналогичным образом можно определять и величину суммы, выдаваемой заемщику, если известна сумма, которая должна быть возвращена, а банк определяет свой доход с использованием учетной ставки. Если при такой операции задаются значения выдаваемой и возвращаемой сумм, можно определить срок займа при заданной учетной ставке:

или

Если заданы значения суммы и срока до оплаты векселя, а также суммы, выплаченной предъявителю векселя (или суммы дисконта), можно определить значение учетной ставки, которую банк использовал при определении своего дохода:

Если необходимо определить значение учетной ставки, обеспечивающей требуемую реальную доходность операции учета в условиях инфляции, можно использовать формулу:

где d - значение учетной ставки, характеризующее требуемую реальную доходность операции учета;

I_p- индекс инфляции за период от даты погашения векселя.

Пример 9. При учете векселя в условиях инфляции должна быть обеспечена реальная доходность, определяемая учетной ставкой 8% годовых. Определить значение учетной ставки, компенсирующей потери от инфляции, при учете векселя, до срока погашения которого осталось 90 дней, если ожидаемый месячный уровень инфляции составит 1,6%, а расчетное количество дней в году 360.

Решение

Индекс инфляции за три месяца составит:

I_n=(1+0,016)³=1,049

Значение годовой учетной ставки, обеспечивающей требуемую реальную доходность операции учета, будет равно:

d=

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. - М.: Финансы и статистика, 1990.

2. Исаев А.М., Шепелева Н.Ю. практика банковского управления и финансового анализа в формулах. – М.: АО «АРГО», 1992.

3. Черкасов В.Е. Учебное пособие по финансово-экономическим расчетам. – М.: АУЗ-БАНК, 1993.

4. Черкасов В.Е. Численные расчеты при учете векселей // Рынок ценных бумаг. – 1994. - № 16 (34).

5. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты.-М.: Метаинформ, 1995.

Сложные ставки процентов

При использовании сложных ставок процентов процентные деньги, начисленные после первого периода начисления, являющегося частью общего срока долга, присоединяются к сумме долга. Во втором периоде начисления проценты будут начисляться исходя из первоначальной суммы долга, увеличенной на сумму процентов, начисленных после первого периода начисления, и так далее на каждом последующем периоде начисления. Таким образом, база для начисления сложных процентов в отличие от использования простых процентов будет увеличиваться с каждым очередным периодом начисления. Если сложные проценты начисляются по постоянной ставке ежегодно в конце года то, наращенная сумма будет равна:

S = P · (1+i)ⁿ, где

P-первоначальная сумма долга;

i - годовая ставка сложных процентов

n – срок финансовой операции в годах

(1+i)ⁿ = k_нс - коэффициент наращения по сложной ставке процентов

Пример 10. Депозит 50 тыс. руб. положен в банк на три года с начислением сложных процентов по ставке 8% годовых. Определить сумму начисленных процентов.

Решение

Сумма депозита с начисленными процентами будет равна:

S=50000·(1+0,08)³=62985,5 руб.

Сумма начисленных процентов составит:

I=S-P=62985,5-50000=12985,6 руб.

Если бы проценты начислялись по простой ставке 8% годовых, сумма их составила бы:

I_n=3·0,008·50000=12000 руб.

Таким образом, начисление процентов по сложной ставке дает большую сумму процентных денег, если срок финансовой операции больше года.

Если срок финансовой операции в годах не является целым числом, наращенная сумма, может быть определена двумя способами:

1) используют формулу S=P(1+i)ⁿ, с соответствующим нецелым показателем степени.

2) Смешанный метод и наращенная сумма определяется по формуле:

S=P(1+i)ⁿ_a·(1+n_вi), где

n = n_a+n_в

n_a- целое число лет

n_в - оставшаяся дробная часть года

Сложные проценты могут начисляться несколько раз в году. При этом годовую ставку процентов, исходя из которой, определяется величина ставки процентов в каждом периоде начисления, называют номинальной годовой ставкой процентов. При сроке долга n лет и начислении сложных процентов m раз в году общее количество периодов начисления будет равно:

N = n · m,

а наращенная сумма будет равна:

S = P · (1+)^n·m, где

j- номинальная годовая ставка процентов

Пример 11. Банк начисляет проценты на вклады ежеквартально по номинальной ставке 10% годовых. Определить сумму процентов, начисленных за два года на вклад 2000 руб.

Решение

Количество периодов начисления равно:

2 · 4 = 8

Следовательно, наращенная сумма составит:

S=2000·(1+)⁸=2436,8 руб.

Сумма начисленных процентов будет равна:

I = 2436,8 – 2000 = 436,8 руб.

Используя формулу для определения наращенной суммы, можно вычислить:

а) срок долга:

б) ставку сложных процентов:

и

в) первоначальную сумму долга (осуществить дисконтирование по сложной ставке процентов):

и

В условиях инфляции годовая ставка сложных процентов, обеспечивающая требуемую реальную доходность кредитной операции в виде годовой ставки r, определяется по формуле:

Н – годовой уровень инфляции

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты.-М.:Финансы и статистика, 1990.

2. Исаев А.М., Шепелева Н.Ю. Практика банковского управления и финансового анализа в формулах.-М.:АО»АРГО»,1992.

3. Черкасов В.Е. учебное пособие по финансово-экономическим расчетам.-М.:АУЗ-БАНК,1993.

4. Черкасов В.Е, Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты.-М.:Метаинформ,1995.

Решение

По приведенной выше формуле:

или 21%

Эквивалентные значения простой i_П и сложной i_С годовых ставок процентов определяются соотношениями:

Годовая ставка процентов, эквивалентная номинальной годовой ставке процентов при их начислении несколько раз в году. Определяется по формуле:

Пример 13. Банк начисляет сложные проценты на вклады по номинальной ставке 12% годовых. Определить доходность вкладов по годовой ставке процентов при их ежемесячном начислении.

Решение

По приведенной выше формуле:

или 12.7%

Расчеты, связанные с финансовой эквивалентностью платежей, применяются при изменении условий контрактов (объединении нескольких платежей в один, замене одного количества платежей на другое, изменении сроков платежей и др.).Для определения эквивалентного значения того или иного платежа для заданной даты (срока) приведения его сумму необходимо умножить на коэффициент приведения.

Обратите внимание, что при дате приведения будет представлять собой коэффициент наращения по заданной ставке процентов, а при дате приведения, меньшей срока платежа, коэффициент приведения будет представлять собой коэффициент дисконтирования. Необходимые формулы и примеры расчетов приведены в рекомендуемой литературе.

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. - М.: Финансы и статистика, 1990.

2. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. - М.: Метаинформ, 1995.

3. Черкасов В.Е. Учебное пособие по финансово-экономическим расчетам. - М.: АУЗБАНК, 1993.

Постоянные финансовые ренты

Если платежи осуществляются нерегулярно и различными суммами, определить наращенную сумму и сумму начисленных процентов можно, применяя последовательно рассмотренные ранее формулы. Если же интервалы между очередными платежами постоянны, и они осуществляются равными взносами, можно сразу определить наращенную сумму для предполагаемого общего срока платежей. Такая последовательность платежей называется постоянной финансовой рентой.

Финансовая рента характеризуется размером платежа, количеством платежей в году, сроком ренты и ставкой , по которой на вносимые платежи начисляются сложные проценты. Зная эти показатели, можно определить наращенную сумму ренты (сумму всех платежей с начисленными процентами).при ежегодных платежах, осуществляемых в конце каждого года, наращенная сумма финансовой ренты будет равна:

где

R – размер очередного платежа;

i – годовая ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах.

Обратите внимание, что эта формула выводится чисто математическим путем как сумма членов геометрической прогрессии, каждый из которых представляет собой очередной взнос с начисленными на него сложными процентами в течение срока, оставшегося до окончания всех платежей.

Пример 14. На депозитный счет в течение 5 лет будут вноситься ежегодно в конце каждого года суммы 50 тыс.руб., на которые будут начисляться сложные проценты по ставке 8 % годовых. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение

Сумма всех взносов с начисленными процентами будет равна:

руб.

Сумма взносов в течение 5 лет составит:

P=5·50000=250000 руб.

Сумма начисленных процентов будет равна:

I = 293330-25000=433330 руб.

Другой обобщающей характеристикой финансовой ренты является ее современная (приведенная) величина, представляющая собой сумму платежей, дисконтированных на момент начала ренты по ставке начисляемых сложных процентов. Формула для определения современной величины постоянной финансовой ренты с выплатами в конце каждого года также получается чисто математически и имеет вид:

Приведенную величину ренты необходимо определять, например, при погашении долгосрочных кредитов.

Из формул для наращенной суммы и приведенной величины постоянной финансовой ренты можно определить размер очередного платежа:

или

Пример 15. Определить размер ежегодных взносов, вносимых в конце каждого года и необходимых для погашения в течение 5 лет долга, равного 500000 руб., если на взносы начисляются сложные проценты по ставке 4% годовых.

Решение

В данном случае известна современная величина постоянной финансовой ренты. Размер ежегодных взносов будет равен:

руб.

Формулы для определения срока годовой ренты, характеристик постоянной ренты с несколькими выплатами в году, а также характеристик других видов рент приведены в рекомендуемой литературе.

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. – М.: Финансы и статистика, 1990.

2. Черкасов В.Е. учебное пособие по финансово-экономическим расчетам. - М.: АУЗ-БАНК, 1993

Планирование погашения долга.

При изучении этой темы обратите внимание, что долг может погашаться разными способами, в зависимости, от выбора которых сумма выплачиваемых процентов (стоимость кредита) будет различной. При погашении единовременным платежом для определения суммы долга с начисленными процентами можно использовать приведенные выше формулы для наращенной суммы.

При погашении основной суммы долга частями его текущее значение будет уменьшаться и, следовательно, сумма процентных платежей также будет уменьшаться. При ежегодных выплатах по долгу с погашением основной суммы долга равными частями размер очередной срочной уплаты будет равен:

У_k=[Д-R(k-1)]i+R , где

У – срочная уплата, которая является суммой двух величин: годового расхода по погашению основного долга и процентного платежа по займу.

i – ставка процента по кредиту

Д – величина кредита.

Пример 16. Кредит в размере 50 тыс. руб. должен быть погашен равными выплатами основного долга в течении 5 лет. Проценты на долг начисляются по ставке 20% годовых. Определить размеры ежегодных расходов заемщика (план погашения долга) и общие расходы по его погашению.

Решение

Годовая уплата основного долга:

руб.

Годовые срочные уплаты:

1-ый год У₁=[50000-10000(1-1)]·0,2+10000=20000 руб.

Процентный платеж I₁=У₁-R=20000-10000=10000 руб.

2-ойгодУ₂=[50000-10000(2-1)]·0,02+10000=20000руб. I₂=18000-10000=8000 руб.

Для последующих лет получаем

У₃ =16000 руб. I₃ = 6000 руб.

У₄ =14000 руб. I₄ = 4000 руб.

У₅ =12000 руб. I₅ = 2000 руб.

Общие расходы по погашению долга составят:

S = 20000+18000+14000+12000=80000 руб.

Сумма выплаченных процентов будет равна:

I = 80000-50000 = 300000 руб.

Еще одним способом погашения долга является погашение равными срочными уплатами, включающими как погашение основной суммы долга, так и выплату процентов. Последовательность срочных уплат в этом случае будет представлять собой постоянную финансовую ренту, современное значение которой должно быть равно сумме долга. Размеры равных срочных уплат при этом определяются по формуле:

У = Д

Пример 17. Кредит на сумму 50000 руб., взятый под 20% годовых, должен быть погашен равными срочными уплатами в течение 5 лет. Определить размеры срочных уплат и общие расходы по погашению долга.

Решение

Годовая срочная уплата

У = 50000руб.

Общие расходы по погашению кредита будут равны:

S = 5 · 16719 = 83595 руб.

Частным случаем погашения долга равными срочными уплатами является потребительский кредит. При котором проценты начисляются по простой ставке, при p выплатах в году сумма выплаченных процентов будет равна:

где

D – сумма кредита;

i – годовая ставка простых по кредиту;

n – срок кредита в годах.

Общие сумма расходов по погашению кредита составит:

S = D+I,

и, следовательно, размер одинаковых очередных взносов будет равен:

У =

Пример 18. Потребительский кредит на сумму 50 тыс. руб. открыт 2 года по ставке 18% годовых. Погашение кредита должно осуществляться равными взносами ежемесячно. Определить стоимость кредита, погашаемую сумму и размер ежемесячных взносов.

Решение

Стоимость кредита (сумма выплаченных процентов) будет равна:

руб.

Погашаемая сумма составит:

S = 50000+9375=59375 руб.

Размер ежемесячных взносов будет равен:

руб.

Обратите внимание, что начисление процентов указанным способом в мировой банковской практике называется «методом 78». Это связано с тем, что для потребительского кредита сроком на 12 месяцев ежемесячный размер погашения будет равен 1/12 его суммы. Следовательно, проценты за 1-й месяц будут начисляться со всей(12/12) суммы кредита, за 2-й месяц – с 11/12 суммы кредита, за 3-й месяц – с 10/12 суммы кредита и так далее до последнего месяца, проценты за кредит, в котором будут браться с 1/12 суммы кредита. Сумма числителей таких дробей будет равна: 12+11+10+9+8+7+6+5+4+3+2+1=78, что и дало название подобному методу начисления процентов.

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. - М.: Финансы и статистика, 1990.

2. Исаев А.М., Шепелева Н.Ю. Практика банковского управления и финансового анализа в формулах. - М.: АО «Арго», 1992.

3. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. - М.: Метаинформ, 1995.

4. Черкасов В.Е. Учебное пособие по финансово-экономическим расчетам. - М.: АУЗБАНК, 1993.

Литература

1. Четыркин Е.М., Васильева Н.Е. Финансово-экономические расчеты. - М.: Финансы и статистика, 1990.

2. Исаев А.М., Шепелева Н.Ю. Практика банковского управления и финансового анализа в формулах. - М.: АО «Арго», 1992.

3. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. - М.: Метаинформ, 1995.

4. Инструктивное письмо ЦБ РФ от 21.07.93 № 46.

5. Черкасов В.Е. Учебное пособие по финансово-экономическим расчетам. - М.: АУЗБАНК, 1993.

6. Бродский В., Горлин Ю. Модель действительной доходности ГКО для клиента//Рынок ценных бумаг. – 1994. - № 1(19).

Решение

Если получаемые денежные поступления не реинвестировались, доходность операции по эффективной годовой ставке процентов будет равна:

-1 = 0,145 или 14,5%

Если получаемые денежные поступления будут тем или иным образом реинвестироваться, в рассмотренной формуле надо учесть общий полученный доход.

При сравнении и выборе наиболее оптимального варианта долгосрочного инвестиционного проекта в международной финансовой практике используются методы инвестиционного анализа, связанные с определением следующих показателей эффективности инвестиций:

чистой текущей стоимости инвестиционного проекта;

внутренней нормы доходности;

срока (периода) окупаемости;

индекса прибыльности (показателя рентабельности).

Чистая текущая стоимость (Net Present Value) инвестиционного проекта представляет собой разность дисконтированных на момент начала инвестирования ожидаемых будущих доходов и расходов. Дисконтирование осуществляется с использованием ставки сложных процентов (см. формулы в теме 3). Обратите внимание, что значение получаемой таким образом чистой приведенной стоимости инвестиционного проекта будет зависеть от ставки сложных процентов, по которой осуществляется дисконтирование. В литературе такую ставку процентов называют также ставкой сравнения или барьерным коэффициентом.

При некотором значении ставки сравнения чистая приведенная стоимость рассматриваемого инвестиционного проекта будет равна нулю . такое значение ставки процентов , по которой осуществляется дисконтирование, называется внутренне нормой доходности ( Interal Rate of Return) инвестиционного проекта. Определить значение внутренней нормы доходности для конкретного инвестиционного проекта можно путем последовательных расчетов или, используя специальные программные средства для ПЭВМ.

Внутренняя норма доходности примерно определяет тот уровень платы за ресурсы инвестирования (проценты за кредит или дивиденды по акциям), при котором будет получена нулевая прибыль. Следовательно, чем больше будет внутренняя норма доходности инвестиционного проекта по сравнению, например, со ставкой процентов по кредитам для инвестирования, тем более прибыльным будет инвестиционный проект с большей внутренней нормой доходности.

Конкретные примеры определения чистой приведенной стоимости и внутренней нормой доходности, а также других показателей, используемых для сравнения инвестиционных проектов, приведены в рекомендуемой литературе. Внимательно изучите соответствующие материалы и прорешайте самостоятельно приведенные в них примеры.

Обратите внимание, что при выборе наилучшего варианта инвестиционного проекта следует учитывать не только количественные показатели, но и такие нефинансовые факторы, как экология. Удобства для населения и др.

Литература

1. Организационные особенности инвестиционной деятельности российских коммерческих банков//Банковское дело. – 1994. - №7.

2. Дамари Р. Финансы и предпринимательство. – Ярославль: Периодика, 1993.

3. Финансовый анализ деятельности фирмы. – М.: ИСТ-СЕРВИС, 1993.

4. Положение об инвестиционном конкурсе по продаже пакетов акций акционерных обществ, созданных в порядке приватизации государственных и муниципальных предприятий //Экономика и жизнь. – 1994. - № 12.

5. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. - М.: Метаинформ, 1995.

Решение

При покупке долларов США на евро необходимо сначала обменять евро на рубли по курсу 36,4

При этой операции 1 рубль равен евро.

Затем полученные рубли надо обменять на доллары США по курсу 29,9. В этой операции 1 доллар США равен 29,9 руб.

Следовательно,1 доллар США равен:

евро (курс продажи).

При продаже долларов США за евро необходимо сначала обменять доллары на рубли по курсу 29,3.

При этом 1 доллар США равен 29,3 рубля.

Затем полученные рубли надо обменять на евро по курсу 37,0.

При этом 1 рубль равен евро.

Следовательно, 1 доллар США равен:

евро (курс покупки).

Таким образом, кросс-курс доллара США и евро будет равен 0,79-0,82.

По времени реализации валютных сделок в мировой практике различают спот-курсы и форвард–курсы валют. Спот-курс – курс, установленный на момент заключения сделки при условии обмена валютами банками-контрагентами на второй рабочий день после заключения сделки. Форвард-курс определяет ожидаемую стоимость валюты через определенный период времени и представляет собой цену, по которой данная валюта продается или покупается при условии ее поставки на определенную дату в будущем.

Теоретический безубыточный форвардный курс определяется следующим образом:

форвард-курсА/В=спот-курсА/В, где A – котируемая валюта;

B - котирующая валюта;

i_A и i_B – процентные ставки по валютам А и В;

t – срок предварительной сделки;

К_А и К_В - длительность процентного года при расчете процентов по валютам А и В.

Реальный форвардный курс будет определяться с учетом спроса и предложения на валютных торгах.

На основе текущих и прогнозируемых курсов валют можно определять доходность различных операций с валютой. А также с конвертацией одних валют в другие. Соответствующие расчетные формулы приведены в рекомендуемой литературе. Внимательно изучите все материалы и решите самостоятельно приведенные в них примеры валютных расчетов.

Литература

1. Банковское дело / Под. ред. О.И.Лаврушена. – М.: Банковский и биржевой НКЦ, 1992.

2. Исаев А.М., Шепелева Н.Ю. Практика банковского управления и финансового анализа в формулах.. - М.: АО «Арго», 1992.

3. Аленичев В.В., Аленичева Т.Д. Страхование валютных рисков, банковских и экспортных коммерческих кредитов. _ М.: АО «АРГО», 1992.

4. Настольная книга валютного дилера. – М.: Верба, 1992.

5. Черкасов В.Е., Плотицына Л.А. Банковские операции: маркетинг, анализ, расчеты. - М.: Метаинформ, 1995.

Простые ставки процентов

Практически все финансово – экономические расчеты связаны с определением процентных денег. Процентными деньгами (процентами) называют сумму доходов от предоставления денег в долг в любой форме (выдача ссуд, открытие депозитных счетов, покупка облигаций, сдача оборудования в аренду и т.п.) Сумма процентных денег зависит от суммы долга, срока его выплаты и процентной ставки, характеризующей интенсивность начисления процентов. Сумму долга с начисленными процентами называют наращенной суммой. Отношение наращенной суммы к первоначальной сумме долга называют множителем (коэффициентом) наращения. Интервал времени, за который начисляют проценты, называют периодом начисления.

При использовании простых ставок процентов сумма процентных денег определяется исходя из первоначальной суммы долга независимо от количества периодов начисления и их длительности по формуле:

I = n · i · P, где

n – срок долга в годах;

i – годовая ставка простых процентов в относительных единицах;

P – первоначальная сумма долга.

Наращенная сумма на каждом периоде начисления будет определяться формулой:

S = P · ( 1 + n · i ) = P · k_нп , где

k_нп– коэффициент наращения.

Приведенная формула используется как для определения суммы вклада с процентами, так и для определения суммы кредита с процентами при его погашении единовременным платежом.

Пример 1.Банк принимает вклады до востребования по простой ставке 8% годовых. Определить сумму процентов на вклад 2000 руб., размещенный на полгода.

Решение

Сумма вклада с процентами:

S = 2000 · ( 1+0,5 · 1,08 ) = 2080 руб.

Сумма начисленных процентов:

I = S – P = 2080 – 2000 = 80 руб.

Сумму начисленных процентов можно также определить по формуле:

I = n ∙ i ∙ P = 0.5 ∙ 0,08 ∙ 2000 = 80 руб.

Если срок долга задается в днях, в приведенную формулу надо подставить выражение:

n= 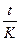, где

t - продолжительность периода начисления в дн