Наращение по сложным процентам с постоянной ставкой

Пусть первоначальная сумма долга равна Р, тогда через один год сумма долга с присоединенными процентами составит Р(1+i), через 2 года P(1+i)(1+i)=P(1+i)², через плет - P(1+i)ⁿ. Таким образом, полу­чаем формулу наращения для сложных процентов:

S = Р (1+i ) ⁿ, (11)

где S - наращенная сумма,

i - годовая ставка сложных процентов,

п - срок ссуды,

(1+ i ) ⁿ - множитель наращения.

На практике обычно используют дискретные про­центы (проценты, начисляемые за одинаковые интервалы времени: год, полугодие, квартал).

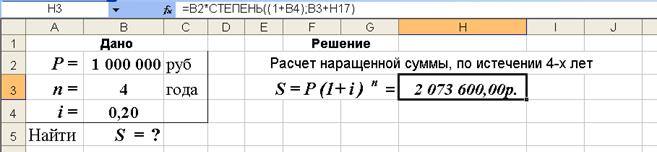
Пример 6.В кредитном договоре на сумму 1 000 000 руб. и сро­ком на 4 года зафиксирована ставка сложных процентов, равная 20% годовых. Определить наращенную сумму.

Известно:

Р = 1 000 000 руб.,

n = 4 года ,

i = 0,20 или 20% .

Найти

S = ? Решение.

1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств. Используем формулу (11):

S = Р (1+ i ) ⁿ =1 000 000*(1+0,2)⁴ = 2 073 600 руб.

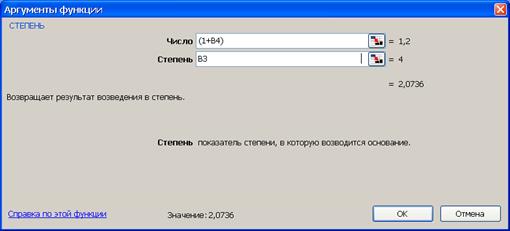
2-й вариант.Для выполнения расчетов по формулам воспользуемся функцией СТЕПЕНЬ (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.9.

а)

б)

Рис.9. Результаты расчета наращенной суммы S (рис. а) и вид диалогового окна СТЕПЕНЬ с введенными данными (рис. б). В ячейку H3 введена формула =B2*СТЕПЕНЬ((1+B4);B3)

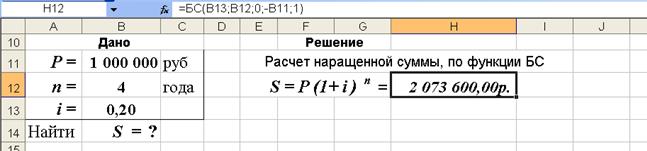
3-й вариант.Для выполнения расчетов по формулам воспользуемся функцией БС (находится в категории Финансовые). Данная функция возвращает результат возведения в степень, рис.10.

Синтаксис функции БС (ставка; кпер; плт; пс; тип). Ее аргументами являются:

ставка – процентная ставка за период;

кпер – общее число периодов платежей по аннуитету;

плт – выплата, производимая в каждый период, ее значение неизменно в течение всего периода выплат. Обычно плт состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если аргумент опущен, должно быть указано значение аргумента пс.

пс – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент пс опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плт.

тип – число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода 1 - в начале периода) Если аргумент «тип» опущен, то он полагается равным 0.

а)

б)

Рис. 10. Результаты расчета наращенной суммы S по функции БС (рис. а) и вид диалогового окна БС с введенными данными (рис. б). В ячейку H12 введена формула =БС(B13;B12;0;-B11;1)

Наращение по сложным процентам при изменении ставки во времени

Если ставка сложных процентов меняется во времени, формула наращения имеет следующий вид:

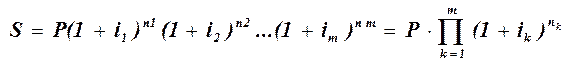(12)

где i₁, i₂,..., i_k - значения ставок процентов, дейст­вующих в соответствующие периоды n₁, п₂,..., n_k времени.

Пример 7.В финансовом договоре зафиксирована переменная ставка слож­ных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% - в третий год, 5% - в четвертый год. Опреде­лить величину множителя наращения за 4 года.

Известно:

i₁ = 0,20 или 20% ,

Δi₁ = 0,10 или 10% ,

n₁ = 2 года ,

Δi₂ = 0,08 или 8% ,

n₂ = 1 год ,

Δi₃ = 0,05 или 5% ,

n₃ = 1 год .

НайтиП(1+ i _k )^{n k} = ?

Решение.

1-й вариант.Вычисления по формулам с помощью подручных вычислительных средств по формуле (12):

П(1+i_k )^{n k} = (1+0,3)² *(1+0,28) * (1+0,25)=2,704.

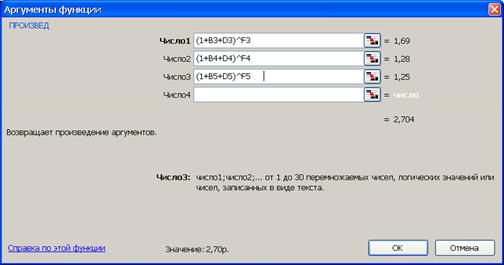
2-й вариант.Для выполнения расчетов по формулам воспользуемся функцией ПРОИЗВЕД (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.11.

а)

б)

Рис. 11. Результаты расчета множителя наращения (рис. а) и вид диалогового окна ПРОИЗВЕД с введенными данными (рис. б). В ячейку J4 введена формула =ПРОИЗВЕД((1+B3+D3)^F3;(1+B4+D4)^F4;(1+B5+D5)^F5)

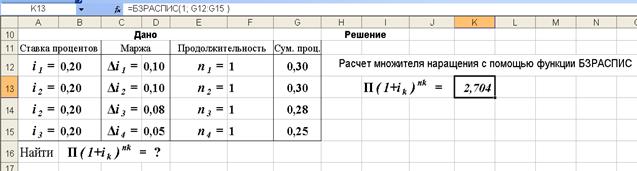
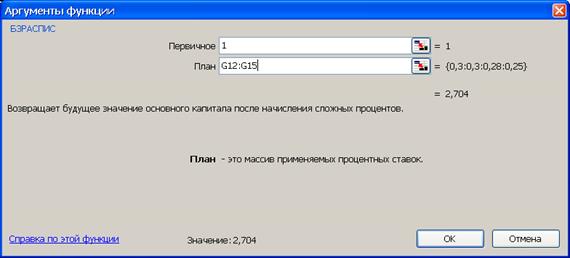
3-й вариант.Предварительно следует подготовить исходные данные по форме представленной на рис. 12а.Для выполнения расчетов следует воспользоваться функцией БЗРАСПИС (находится в категории Финансовые). Данная функция возвращает будущее значение основного капитала после начисления сложных процентов с переменной ставкой, рис.12. Поскольку здесь рассчитывается множитель наращения, то в качестве первоначальной суммы вводится 1 (см. рис 12б).

а)

б)

Рис. 12. Результаты расчета множителя наращения (рис. а) и вид диалогового окна БЗРАСПИС с введенными данными (рис. б). В ячейку J13 введена формула =БЗРАСПИС(1; G12:G15)

Синтаксис функции БЗРАСПИС (первичное; план). Аргументы функции:

первичное – действительное число, задающее первоначальную стоимость инвестиции;

план – массив значений, содержащих процентные ставки.

Напомним, что для вычисления будущей стоимости с постоянной ставкой используется функция БС.