Реинвестирование по простым ставкам

На практике при инвестировании средств в краткосрочные депозиты иногда прибегают к неоднократному последовательному повторению наращения по простым процентам в пределах заданного общего срока.

Фактически это означает реинвестирование средств, полученных на каждом этапе наращения, с помощью постоянной или переменной ставок.

Наращенная сумма для всего срока составит:

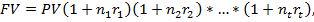
где r_t – размер ставок, по которым проводится реинвестирование.

Наращенная сумма для всего срока (если промежуточные сроки начисления и ставки не изменяются во времени)

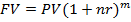
где m – количество повторений реинвестирования.

Определение срока ссуды и величины процентной ставки

В практике банковских расчетов бывают ситуации, когда срок финансовой операции прямо в условиях финансовой сделки не оговорен или когда данных параметр определяется при разработке условий финансовой сделки.

Срок финансовой операции при известной процентной ставке r и величине начисленных процентов определяется по формуле:

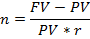
Если срок сделки необходимо определить в днях, то появляется временная база (Т) в качестве сомножителя:

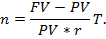
Степень доходности операции (величину процентной ставки) по заданным параметрам определяется по формуле:

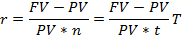
Дисконтирование по простым процентам

При заключении финансовых соглашений часто приходится решать задачу, обратную задаче нахождения наращенной суммы.

По заданной сумме FV, которую предполагают получить через время t, требуется определить величину капитала PV, который необходимо инвестировать в данный момент, чтобы через время t при постоянной процентной ставке получить сумму FV.

Движение денежных средств от будущего к настоящему называется дисконтирование (говорят, что капитал дисконтируется или учитывается).

Величина удержанных процентов называется дисконтом. Капитал PV, найденный дисконтированием суммы PV называется приведенной (современной, текущей, капитализированной) стоимостью.

При математическом дисконтировании решается задача нахождения такой величины капитала PV, которая через n лет при наращении по простым процентам по ставке r будет равна FV.

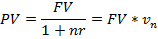
где 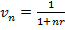- дисконт фактор (дисконтный множитель) или коэффициент дисконтирования (величина, обратная множителю наращения).

Разность между FV и PV называется дисконтом (D).

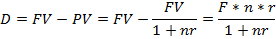
Банковское дисконтирование или банковский учет применяется при операции по так называемому учету векселей банком или другим финансовым учреждением.

Банковский учет векселей рассматривается в отдельном разделе.

Тема 4. Функции сложного процента

Функция №1 – будущая стоимость единицы

Формула сложных процентов

Применение схемы сложных процентов целесообразно тогда, когда проценты не выплачиваются по мере их начисления, а присоединяются к первоначальной сумме долга.

Присоединение начисленных процентов к сумме долга, которая служит базой для их начисления, называется капитализацией процента.

Если процентные деньги не выплачиваются сразу по мере их начисления, а присоединяются к первоначальной сумме долга, то долг, таким образом, увеличивается на невыплаченную сумму процентов и последующее начисление процентов происходит на увеличенную сумму долга.

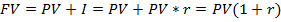– за один период начисления,

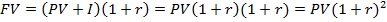– за два периода начисления.

(подставляем вместо I=PV*r)

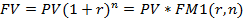- за n периодов начисления.

где FV - наращенная сумма долга,

PV – первоначальная сумма долга,

r - ставка процентов в периоде начисления,

n - количество периодов начисления,

FM1(r,n)=(1+r)ⁿ – множитель наращения сложных процентов (будущая стоимость единицы).

Сложные проценты отличаются от простых базой начисления.

Простые проценты начисляются все время на одну и ту же первоначальную сумму, т.е. база начисления является постоянной величиной.

Сложные проценты начисляются на увеличивающуюся с каждым периодом начисления базу.

Коэффициенты (множители) наращения зависят от процентной ставки и числа периодов наращения. Их можно определить по специальным таблицам.

Экономический смысл множителя наращения состоит в том, что он показывает, чему будет равна одна денежная единица (рубль, доллар, пр.) через n периодов при заданной процентной ставке r.

Сложные проценты

Простые проценты

FV

t

Рис. Наращение по простым и сложным процентам

Из рис. видно, что при краткосрочных ссудах (n<1) начисление по простым процентам предпочтительнее, чем по сложным процентам. При сроке ссуды в 1 год разница отсутствует. При среднесрочных и долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам выше, чем по простым.

При любом r:

Если 0<n<1, то (1+nr)>(1+r)ⁿ

Если n=1, то (1+nr)=(1+r)ⁿ

Если n>1, то (1+nr)<(1+r)ⁿ

Финансовое соглашение может предусматривать плавающие процентные ставки

Пусть n₁, n₂, …, n_m следующие друг за другом периоды. На период n_k установлена процентная ставка r_k.

При капитализации процентов наращенная сумма за время определяется по формуле: