Начисление процентов за дробное число лет

Достаточно обыденными являются финансовые контракты, заключаемые на период, отличающийся от целого числа лет. В этом случае проценты могут начисляться одним из двух методов:

· по схеме сложных процентов:

· по смешанной схеме (используется схема сложных процентов для целого числа лет и схема простых процентов - для дробной части года):

где w - целое число лет;

f - дробная часть года.

Поскольку f < 1, то (1 + f ∙ r) > (1 + r)^f, следовательно, наращенная сумма будет больше при использовании смешанной схемы. Можно показать, что при малых r наибольшая величина разности между (2.10.7) и (2.10.8) достигается при f 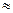0,5.

Пример 2.22. Банк предоставил ссуду в размере 10 тыс. руб. на 30 месяцев под 30% годовых на условиях ежегодного начисления процентов. Какую сумму предстоит вернуть банку по истечении срока?

По формуле (2.10.7): F_n = 10 ∙ (1 + 0,3)^2+0,5 = 19,269 тыс. руб.

По формуле (2.10.8): F_n =10 ∙ (1 + 0,3)² ∙ (1 + 0,3 ∙ 0,5)= 19,435 тыс. руб.

Таким образом, в условиях задачи смешанная схема начисления процентов более выгодна для банка.

Встречаются финансовые контракты, в которых начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. В этом случае также возможно использование двух схем:

а) схема сложных процентов:

б) смешанная схема:

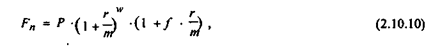
где w - целое число подпериодов в n годах;

f - дробная часть подпериода ;

m - количество начислений в году;

r - годовая ставка.

Обращаем внимание читателя на то, что в приведенных алгоритмах показатели w и f имеют разный смысл. Так, в формуле (2.10.9) w означает целое число лет в и годах, а f - дробную часть года и поэтому n = w + f. Однако в формуле (2.10.10) w означает целое число подпериодов в п годах, а f - дробную часть подпериода и поэтому n = (w + f)/m. Иными словами, при пользовании этими формулами нужно отдавать себе отчет в том, о каком базисном периоде идет речь.

Пример 2.23.Банк предоставил ссуду в размере 120 тыс. руб. на 27 месяцев (т.е. 9 кварталов, или 2,25 года) под 16% годовых на условиях единовременного возврата основной суммы долга и начисленных процентов. Проанализировать, какую сумму предстоит вернуть банку при различных вариантах и схемах начисления процентов: а) годовое; б) полугодовое; в) квартальное.

а) Годовое начисление процентов

В этом случае продолжительность ссуды не является кратной продолжительности базисного периода, т.е. года. Поэтому возможно применение любой из схем, описываемых формулами (2.10.7) и (2.10.8) и значениями соответствующих параметров: n = 2,25; w = 2; f = 0,25; r = 0,16.

· При реализации схемы сложных процентов:

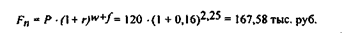
· При реализации смешанной схемы:

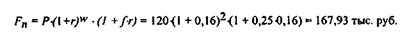
б) Полугодовое начисление процентов

В этом случае мы имеем место с ситуацией, когда начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. Следовательно, нужно воспользоваться формулами (2.10.9) и (2.10.10), когда параметры формул имеют следующие значения: т = 2; w = 4; f = m ∙ п - w = 2 ∙ 2,25 - 4 = 0,5; r = 0,16.

· При реализации схемы сложных процентов:

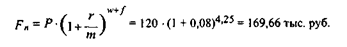
· При реализации смешанной схемы:

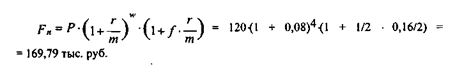
в) Квартальное начисление процентов

В этом случае т =2; w = 9; f = 0, т.е. продолжительность ссуды равна целому числу подпериодов. Поэтому формулы (2.10.9) и (2.10.10) дают один и тот же результат:

F_n = 120 ∙ ( 1 + 0,04)⁹ = 170,8 тыс. руб.

Здесь фактически пользуемся обычной формулой наращения сложными процентами (2.10.3), в которой n = 9, а r = 0,16/4 = 0,04.