Управление подобными рисками.

Прогнозирование

Задача. В ближайшее время состоятся выборы Президента РФ и в Гос Думу. Какие кредитные будут у банка?

1.Диверсификация источников финансирования (много источников финансирования), возникает некая стабильность.

15.4. Невозможность получения кредита.

Причины:

1) плохая кредитная история

2) низкий или отрицательный Гудвил

3) низкая доходность операций предприятия, которая не обеспечивает погашение кредитов, предлагаемых банком (текстильная отрасль в Ивановской области)

4) отсутствие предложений со стороны банков (банкам выгоднее производить иные операции)

15.4.1. Методы управления рисками:

1. Использовать другие источники финансовых средств (собственный капитал, указать способы альтернативных источников финансирования).

2. Лимитирование. Уменьшить объем спроса денежных средств. В этом случае банк понимает, что меньше объем – меньше риск; наличие системы лимитирования увеличивает нашу надежность в глазах кредитора.

3. Резервирование (переход на иные способы установления хозяйственных взаимоотношений) => бартер => переработка (толлинговая схема или работа на давальческом сырье).

Это крайние меры, использование которых указывает на критическое состояние предприятия.

Толлинг – переработка, при которой товарное сырье/продукция пересекает границы (возникают таможенные взаимоотношения).

Имитационное моделирование рисков.

Стресс-тестинг

Стресс тестинг– проведение исследований возможных сценариев развития ситуации в деятельности хоз субъекта с учетом возможных реакций лиц, принимающих решение, на эти сценарии.

Гибкие бюджеты – это процесс построения бюджетов предприятия с учетом вариативности сценариев в развитии ситуации.

-умеренное

-агрессивное

-консервативное

В экономике сложилось классическое представление о прогнозных величинах как о детерминированных величинах, то есть прогнозное значение есть какое-то конкретное значение финансового показателя. Учитывая несостоятельность такого подхода, одним из путей выхода предлагается наряду с этими значениями указывать характеристику разброса допустимых значений относительно указанного.

-дисперсия

-среднее квадратическое отклонение

-показатели вариации (размах вариации)

Дисперсия вычисляется лишь в случае известного распределения вероятностей. Вычислить распределение вероятностей прогнозируемой величины бывает достаточно сложно.

Пример.

NPV – чистая распределенная прибыль

NPV = 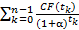, где

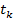– моменты производства платежей

α – ставка дисконтирования

CF( 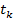) – значение величины платежа в момент времени 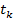(Cash Flow)

1 вариант.

CF( 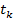) = 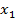+ +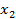..+ 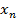, где 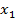, ,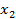.., 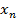– случайные независимые величины

CF(t_k) – N(a;σ) – нормальное распределение

CF(t_k) – случайная величина

2 вариант.

CF(t_k) = x₁x₂..x_n – мультипликативная величина , ненормальное распределение

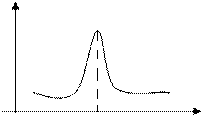
Если x_i представляется в виде x_i=eu_i, а u_i подвержены условиям центральной предельной теоремы, то CF(t_k) будет иметь распределение, принадлежащее семейству логарифмически нормальных распределений.

Плотность данного распределения:

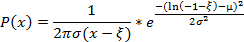
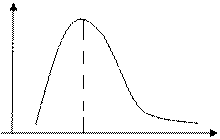ξ

Время производства платежа

Время производства платежа(t_k) также может случайной величиной, тогда необходимо выяснить распределение этой случайной величины.

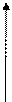p =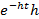

t t_k

d – доля платежей, которые производятся в срок

(1-d) – доля платежей, которые в срок не производятся

Вопрос о задержке платежа аналогичен вопросу о продолжительности жизни человека, который рассматривается в страховании. Определением страховых ставок расчета продолжительности жизни (исследование страховых случаев) занимается актуарная математика.Всеобъемлющий раздел науки – страховое дело.

Гипотеза Муавра.

Интенсивность смерти в зависимости от возраста.

h(t) – интенсивность

h(t)

0 100

Функция распределения смерти

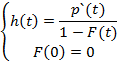
F(t) = 1 - 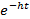– экспоненциальная функция

Если интенсивность производства платежа при его задержке постоянна, то плотность распределения задержки экспоненциальна.

Если h(t) – степенная функция, например, в случае, если интенсивность платежей увеличивается в связи с нашими жесткими действиями по управлению дебиторской задолженностью), то область распределения времени платежа имеет вид:

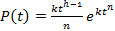, (h(t) = k )

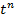Закон Эриама. Пусть длина очереди n, время обслуживания каждого клиента имеет экспоненциальное распределение с плотностью p(t)= 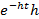, тогда время обслуживания

всей очереди распределено по закону Эриама с плотностью 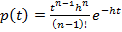. Частный случай гамма-распределения.

Время обслуживания каждого клиента независимо друг от друга.

16.4. Метод Монте-Карло (метод вычисления интегралов).

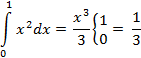
(25+36+49+100+121+2*144+2*289+324+800+882+484+625+3*676+784+2*841) * 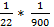= = 0,44

Неточность в вычислениях потому, что распределение неравномерно.

Более точный результат можно получить, если использовать счетчики случайных чисел.

Для Excel в скобках любое значение между 0 и 1

= сл чис ( )

=сл чис ( ) = ̺̺ * ̺ = ср знач (массив)

Растянуть на 5 000 знаков.

Для того, чтобы организовать выборку с заданными наперед распределениями, достаточно знать набор равномерно распределенных величин. Известно преобразование Смирнова

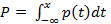, где

p(t) – плотность заданного распределения. Если Р – равномерно распределенная величина на [0;1], то величина x будет иметь распределение с плотностью p(t).

В электронных таблицах выражение x(P) реализовано при некоторых значениях p(t).

Например, для нормально распределения

= норм обр (сл чис ( );a;σ) числа а и σ ввести средние, дисперсия

= гаммаобр (сл чис ( );d;β)

=бэтаобр (сл чис ( );α;β)

Бэтта–распределение – распределение случайной величины, значения которой лежат на определенном отрезке ( [0;1] для Excel).

Частный случай бэтта-распределения – равномерное.

Имеет вид:

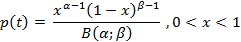
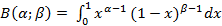- функция Эйлера второго рода (β-функция).