Операция математического дисконтирования

Операция математического дисконтирования – нахождение для каждой денежной суммы ее современной стоимости (в момент времени t o = 0).

St – денежная сумма в момент времени t

So – современная стоимость

α – безрисковая ставка процента

– дисконт-фактор

Задача. Рассматривается следующий проект использования денежных средств. Сейчас мы инвестируем 100 000 рублей. Через год наш доход составит 80 000 рублей, а еще через год 60 000 рублей. Определить выгодность подобного рода проекта.

Подзадача. Издержки по проекту А: переменные - 2 рубля на штуку продукции; постоянные – 50 000 рублей в месяц. Предлагается произвести 100 000 единиц продукции, каждую из которой заказчик готов купить за 3 рубля 50 копеек за штуку. Определить выгодность сделки.

350 000 – 200 000 – 500 000 = 150 000 – 500 000 = -350 000

Говорить о выгодности финансового потока бессмысленно, пока не произведены расчеты альтернативных проектов.

Банковский вклад 6% - альтернативный проект, с которым мы будем сравнивать предложенный проект.

1 подход. Net Present Value (чистая приведенная прибыль).

Чистая приведённая стоимость (чистая текущая стоимость, чистый дисконтированный доход, англ. Net present value, принятое в международной практике анализа инвестиционных проектов сокращение — NPV или ЧДД) — это сумма дисконтированных значений потока платежей, приведённых к сегодняшнему дню.

– чистая приведенная прибыль NPV; денежная сумма, которая будет положена в банк, даст нам ровно столько денег, сколько весь проект в целом. Если число больше 0, то проект выгоден больше по сравнению с вложением денег в банк.

2 подход. Найдем ту скорость наращивания денежных средств, которая соответствует нашему проекту (внутренняя ставка доходности – IRR).

Внутренняя норма доходности (англ. internal rate of return, общепринятое сокращение — IRR (ВНД)) — это процентная ставка, при которой чистый дисконтированный доход (NPV) равен 0. NPV рассчитывается на основании потока платежей, дисконтированного к сегодняшнему дню.

– нулевое приращение активов по сравнению с процентной ставкой нашего проекта.

Способы решения уравнения.

Пригласить специалиста, чтобы он решил уравнение.

Метод дихотомии.

Берутся 2 ставки, одна должна давать заведомый минус, другая – заведомый плюс (6% - плюс, 5% - минус).

Метод дихотомии состоит в том, что мы каждый раз вычисляем значение NPV в середине отрезка, значения NPV в концах которого имеют разные знаки.

12.2.2. С помощью таблицы

-100

80 [массив]

= ВСД ([массив];0,1) = 0,27

-10 + 8у + 6y² = 0

3y² + 4y – 5 = 0

D = 16 +60 = 76

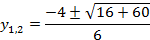
у = 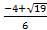= = 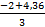= =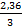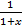> x = 0,27

27% - нормальная скорость наращения денежной суммы

Время как параметр риска.

1.Если финансовые потоки согласованы так, что может возникнуть промежуток времени, в течении которого необходимо произвести выплаты, однако денежных средств недостаточно, но они ожидаются. Тогда возможны следующие варианты:

1) частичный или полный отказ от производства (уменьшение прибыли)

2) получение кредитного заимствования => выплата процента (уменьшение прибыли)

Управление такого рода рисками – оптимальное согласование моментов выплат денежных сумм.

2. Учитывая временную стоимость денег, необходимо иметь в виду, что более ранние по времени выплаты имеют большую ценность (правило финансиста – бери раньше, отдавай позже).

Управление риском в связи с этим основывается на организации мероприятий, не позволяющих дебиторам задерживать платежи.

3.При планировании инвестиционных проектов необходимо учитывать фактор времени в виду того, что существуют так называемые процентные риски.

13.1. Кредитные риски.

Сущность риска – получение денежной суммы от дебитора не в указанный договором момент времени и не в соответствующем объеме.

Как работать с дебиторами.