Модель оценки доходности финансовых активов САРМ

Модель описывает зависимость рыночного риска и доходности финансовых активов. Теория САРМ (Capital Assets Pricing Model)была разработана Уильямом Ф. Шарпом и опубликована им в 1964 году. Он получил нобелевскую премию по экономике за исследования в области ценообразования финансовых активов.

Модель основана на предпосылках о существовании идеальных рынков капитала.

1. Главная цель инвестора – максимизация прироста своего достояния.

2. Все инвесторы могут давать и брать ссуды неограниченного размера по безрисковой процентной ставке.

3. Ожидания инвесторов относительно изменений показателей акций одинаковы.

4. Все активы абсолютно делимы и совершенно ликвидны.

5. Не существует трансакционных затрат.

6. Не учитываются налоги.

7. Инвесторы предполагают, что их деятельность не влияет на уровень цен.

8. Количество финансовых активов заранее определено и фиксировано.

Оптимальный выбор инвестора определяется как пересечение кривых безразличия, отражающих предпочтения данного инвестора, и совокупности эффективных портфелей, которые могут быть сформированы на данном рынке. Предполагалось, что все активы, входящие в оптимальный портфель – рисковые. Тем не менее, можно выделить безрисковые финансовые активы – те, по которым нет риска дефолта, такими активами принято считать государственные ценные бумаги (в условиях стабильности государственного финансового рынка и государственных финансов в целом). Если инвестор включит в портфель безрисковые активы это приведет к изменению структуры портфеля и именит его окончательный инвестиционный выбор, выражающийся в структуре оптимального портфеля.

Ллиния рынка капитала – CML –это касательная от точки K_rf, характеризующей безрисковый актив (его доходность K_rf, риск s = 0) к эффективному множеству портфелей.

Определим доходность и риск оптимального портфеля ценных бумаг (M), сформированного из безрискового актива и совокупности рисковых активов.

Доходность портфеля К_р можно определить по формуле:

К_р = x*K_rf + (1-х)K_M, где

K_rf - доходность безрискового актива,

х – доля безрискового актива в портфеле,

K_M - доходность портфеля, состоящего из рисковых активов.

Уровень риска s_р портфеля может быть определен, как его СКО, для расчетов можно воспользоваться формулой:

s_р = (1-х)s_м , где

s_р – СКО доходности портфеля,

s_м – СКО доходности портфеля, состоящего только из рисковых активов,

х – доля безрисковых активов в портфеле.

Уравнение CML : K_F = K_rf + (K_М - K_rf )/(s_р/s_м).

Степень наклона (крутизны) CML показывает, какую доходность могут получить инвесторы в зависимости от принятых рисков, ее можно рассчитать следующим образом: (K_М - K_rf )/s_м. Эта величина отражает рыночную цену полностью диверсифицированных портфелей.

Рисковость ценной бумаги определяется ее бета-коэффициентом. Этот коэффициент характеризует изменчивость доходности конкретной ценной бумаги относительно доходности рынка ценных бумаг.

Предполагается, что некоторая «средняя» акция имеет b-коэффициент равный 1. Если изменчивость доходности данной ценной бумаги меньше, чем у «средней» акции, то ее b-коэффициент меньше единицы.

Связь между риском и доходностью конкретной ценной бумаги называют уравнением линии рынка ценных бумаг – SML. Оно выглядит следующим образом: K_i = K_rf + (K_М - K_rf )*b_i

K_i – требуемая доходность i-ой акции,

K_rf - доходность безрискового актива,

K_M - доходность рыночного портфеля,

b_i - b-коэффициент i-ой акции.

(K_М - K_rf )-рыночная премия за риск или цена риска для средней акции.

На требуемый уровень доходности влияет инфляция, но она одинаково сказывается на всех ставках доходности. В каждой из этих номинальных ставок можно выделить две составляющих:

- реальный уровень доходности,

- инфляционная премия.

Крутизна линии рынка ценных бумаг отражает отношение инвесторов к риску: чем круче наклон, тем меньше инвесторы склонны к риску.

Рассмотрим основные различия CML и SML:

1. Для линии рынка капитала риск характеризуется СКО – показатель общего риска. Для линии рынка ценных бумаг показателем риска является бета-коэффициент – показатель специфиического риска.

2. При равновесии только полностью диверсифицированные портфели находятся на линии рынка капитала, а отдельные ценные бумаги лежат под ней. Все ценные бумаги и все портфели находятся на линии рынка ценных бумаг.

Как уже было сказано, предполагается, что некоторая «средняя» акция имеет b-коэффициент равный 1. Характеристики этой «средней» акции будут меняться в зависимости от изменения рыночной ситуации. При изменении ситуации на рынке показатели «средней» акции меняются в том же направлении и на ту же величину. b-коэффициент большинства рыночных акций меняется от 0,75 до 1,5.

Например, b-коэффициент “Procter&Gambel” равен 1, “Harley-Davidson” – 1,6.

b-коэффициент портфеля ценных бумаг рассчитывается по формуле средней арифметической взвешенной.:

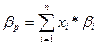, где

х_i – доля i-ой ценной бумаги в портфеле,

Если в портфель добавляются ценные бумаги, имеющие b>1, то уровень риска портфеля повышается, и, наоборот, если добавляются ценные бумаги, имеющие b<1, то уровень риска портфеля снижается.

Учитывая, что предпосылки модели САРМ не соответствуют ситуации, которая существует на практике, модель нуждается в проверке на реалистичность.

Сложность такой проверки заключается в том, что модель использует ожидаемые данные, а ожидания инвесторов не обязательно совпадут с практической ситуацией, которая сложится на рынке. Поэтому проверить модель, используя исторические данные невозможно.

В результате анализа ожиданий инвесторов, реальной ситуации на рынке и результатов, которые принесли те или иные решения инвесторов были получены следующие выводы:

1. Существует тесная прямая связь между доходностью и риском, но на практике наклон линии обычно ниже, чем предсказываемый моделью САРМ.

2. Связь риска и доходности действительно является линейной.

3. САРМ предполагает, что риск, который может быть устранен с помощью диверсификации портфеля, не имеет значения, а на практике он также оказывает влияние на принятие решений.

4. Вызывает сомнения, что инвесторы будут действовать в будущем так, как планируют в настоящем.

5. САРМ совершенно не подходит для анализа рынка облигаций, а при анализе рынка акций дает хорошие результаты.

Сама по себе CAPM является изящной научной теорией, имеющей солидное математическое обоснование. Для того, чтобы она “работала” необходимо соблюдение таких заведомо нереалистических условий как наличие абсолютно эффективного рынка, отсутствие транзакционных издержек и налогов, равный доступ всех инвесторов к кредитным ресурсам и др. Тем не менее столь абстрактное логическое построение получило практически всеобщее признание в мире реальных финансов. Крупнейшие рыночные институты, такие как инвестиционный банк Merril Lynch, регулярно рассчитывают β-коэффициенты всех крупных компаний, котирующихся на фондовых биржах. Отсутствие в России сформированной финансовой инфраструктуры пока еще препятствует использованию всего потенциала, заложенного в данную модель. Поэтому рассмотрим пример расчета уровня ожидаемой доходности с использованием подхода САРМ на фондовом рынке США.

Компания, имеющая β-коэффициент 2,5, собирается привлечь дополнительный собственный капитал путем эмиссии обыкновенных акций. Уровень безрисковой процентной ставки составляет 6,25%, средняя доходность рынка, рассчитанная по индексу S&P 500, – 14%. Для того, чтобы сделать свои ценные бумаги привлекательными для инвесторов, компания должна предложить по ним ежегодный доход не ниже 25,625% (6,25 + 2,5 * (14 – 6,25)). Размер премии за риск составит 19,375%. Столь существенные ограничения, накладываемые рынком на возможности снижения цены капитала, устанавливают предел доходности инвестиционных проектов, которые компания собиралась финансировать привлекаемым капиталом: внутренняя норма доходности этих проектов должна быть не ниже 25,625%. В противном случае NPV проектов окажется отрицательной, то есть они не обеспечат увеличения стоимости предприятия. Если бы β-коэффициент компании был равен 1,5, то размер премии за риск составил бы 11,625% (1,5 * (14 – 6,25)), то есть цена нового капитала составила бы лишь 17,875%. Полученные результаты могут быть представлены на графике, показывающем зависимость требуемой инвесторами нормы доходности при заданных значениях β-коэффициента, безрисковой процентной ставки (r_f) и средней рыночной доходности (r_m). Данный график отражает линию рынка ценных бумаг (Security Market Line, SML).

Использование CAPM дает финансовому менеджеру инструмент прогнозирования издержек по привлечению нового капитала для реализации инвестиционных проектов. Финансы любого предприятия являются открытой системой, поэтому, планируя свои капиталовложения, оно обязано учитывать при этом конъюнктуру финансового рынка. Менеджеры компании могут абсолютно ничего не знать об индивидуальных особенностях и личных предпочтениях потенциальных инвесторов. Это не освобождает их от обязанности предугадать главную потребность любого инвестора – получить доход, компенсирующий риск инвестиций. В этом им может помочь использование модели оценки финансовых активов.

3.5. Теория ценообразования опционов

Опцион — это контракт, дающий владельцу, или держателю опциона, право , купить или продать определенный актив по некоторой, заранее оговоренной течение определенного промежутка времени. Опционы могут быть выписаны фактически на любой актив, однако наибольшее распространение они получили в связи с операциями с недвижимостью и ценными бумагами. Самая важная характеристика опциона заключается в том, что держатель опциона не обязан совершать предусмотренных в контракте действий, т. е. опцион дает собственнику право, но не обязанность купить или продать актив. Таким образом, если в случае исполнения опциона могут возникнуть отрицательные последствия, владелец опциона предпочтет отказаться от его исполнения.

Опционы существуют уже в течение многих лет, однако до недавнего времени их использование не было широко распространено. Раньше условия опционных контрактов должны были согласовываться по каждой сделке непосредственно покупателем и продавцом. Это осложняло поиск контрагентов, поэтому в 1973г. была создана первая опционная биржа — «Chicago Board Option Exchange» (СВОЕ). Это позволило снизить трансакционные затраты.

Опционы используются достаточно давно, но формальная модель ценообразования опционов Блэка-Фишера была сформулирована только в 1973 году.

В практике финансового менеджмента опционы сегодня активно применяется в сделках с новыми высокотехнологичными продуктами, например, на рынке интернет-технологий.

3.6. Теория арбитражного ценообразования (АРТ)

В середине 70-х годов Стивеном Россом была предложена модель арбитражного ценообразования, которая позволяет учесть риск более полно, чем САРМ. Теория арбитражного ценообразования в отличие от САРМ является многофакторной моделью. Она позволяет учесть любое количество факторов риска. Акции различных компаний неодинаково реагируют на эти факторы, поэтому необходимо учитывать различные составляющие риска отдельно.

Такими отдельными факторами риска являются, например, экономическая ситуация в стране, темп инфляции, бюджетные показатели, налоговые изменения и т.д.

Математически модель арбитражного ценообразования выглядит следующим образом:

K_i = K_i^*+ (F₁ – F₁^* )*b_i1 +…+(F_j – F_j^* )*b_ij +e_i , где

K_i – фактическая доходность i-ой акции,

K_i ^*– ожидаемая доходность i-ой акции,

F_j - фактическое значение экономического фактора j,

F_j ^* - ожидаемое значение экономического фактора j,

b_ij - влияние чувствительности акции i к экономическому фактору j,

e_i - влияние специфических факторов на изменение фактической доходности акции i.

Концепция арбитражного ценообразования использует меньшее количество допущений, чем САРМ и более детально учитывает влияние внешней среды. Но теория имеет существенный недостаток, в ней нет ограниченного списка факторов, поэтому невозможно учесть влияние полностью, всегда останутся факторы, которые влияют на фактическую доходность акций, но не были учтены при анализе. Кроме того, возможно, что влияние неучтенного фактора достаточно сильно, чтобы рассматривать полученные без его учета результаты, как достоверные.

Концепция арбитражного ценообразования развивается и, возможно, в будущем основные недостатки модели будут учтены за счет внесения в модель корректив.

Вопросы и задачи к главе 3

1. В чем состоит анализ дисконтированного денежного потока? Перечислите его основные этапы.

2. Какой основной вывод был сделан М. Миллером и Ф. Модильяни при анализе структуры капитала фирмы?

3. Какое влияние в условиях идеальных рынков, по мнению М. Миллера и Ф. Модильяни оказывает политика выплаты дивидендов на стоимость фирмы?

4. Как можно снизить совокупный риск инвестора согласно теории портфеля?

5. Функцией каких переменных является требуемая доходность рисковых активов согласно теории САРМ?

6. Что понимается под «эффективностью» в гипотезе эффективности рынков? Охарактеризуйте основные формы эффективности.

7. Какие показатели связывает модель САРМ?

8. Перечислите основные предпосылки модели САРМ?

9. В чем сходства и различия линии рынка капитала и линии рынка ценных бумаг?

10. Что такое безрисковый финансовый актив?

11. Что такое бета-коэффициент? Почему бета-коэффициент «средней акции» равен 1?

12. Как влияет на риск портфеля добавление в него ценных бумаг бета-коэффициент которых больше 1? меньше 1?

13. Каково практическое значение модель САРМ?

14. В чем основное отличие теории арбитражного ценообразования от САРМ?

15. Назовите основные достоинства и недостатки теории арбитражного ценообразования.

Задачи

1. Определите доходность портфеля, состоящего на 30% из безрискового актива, доходностью 15% и из рисковых ценных бумаг, объединенных в портфель с общим уровнем доходности 25%.

2. Определите уровень риска портфеля, состоящего на 30% из безрискового актива, доходностью 15% и из рисковых ценных бумаг, СКО которых составляет 20.

3. Определите требуемую доходность акции, если известно что доходность безрискового актива 10%, доходность рыночного портфеля 18%, а бета-коэффициент акции равен 1,3. Чему будет равна требуемая доходность той же акции, если ее бета коэффициент составит 1,8.

4. Акция Х имеет коэффициент бета, равный 1,3; безрисковая доходность составляет 8%, премия за рыночный риск – 7%. какова требуемая норма прибили по акции Х.

5. Определите бета-коэффициент портфеля ценных бумаг, состоящего из акций фирмы «Ромашка» на сумму 30 тыс. руб., бета-коэффициент акций равен 1,2; акций фирмы «Георгин» на сумму 50 тыс. руб., бета-коэффициент акций равен 1,6; акций фирмы «Тюльпан» на сумму 20 тыс. руб., бета-коэффициент акций равен 0,8. Сравните уровень риска портфеля со среднерыночным.

Литература

1. Базовый курс по рынку ценных бумаг. – М, ИАУУ НАУФОР - 1999

2. Басовский Л.Е. Финансовый менеджмент. – М.: Инфра-М, - 2002;

3. Бригхем Ю., Гапенски Л. Финансовый менеджмент. - СПб.: Экономическая школа, 1997;

4. Касимов Ю.Ф.Основы теории оптимального портфеля ценных бумаг. – М.: Филинъ, 1998. – 142 с.;

5. Колб Р.Б., Родригес Р. Дж. Финансовый менеджмент. – М.: Издатество «Финпресс»,2001;

6. Лытнев О. Курс лекций «Основы финансового менеджмента» - 2000, http://www. cfin.ru

7. Станиславчик Е.Н. Основы финансового менеджмента. – М.: «Ось-89»,2001.