Метод экономических интервалов

Для пояснения сущности этого метода вновь обратимся к выражению (4-3). Зададимся вопросом, как приведенные затраты на линию электропередачи, выполненную проводом сечением F_i зависят от тока 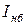, протекающего в линии в часы наибольших нагрузок.

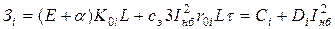(3.6)

Как видно из этого выражения, эта зависимость представляет собой квадратичную параболу (рис.4.2, кривая 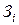). При этом величина 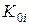будет определять положение параболы по высоте (коэффициент 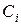), а величина 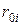- крутизну параболы (коэффициент ).

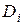Рассмотрим еще два варианта сооружения этой линии, один – с сечением провода 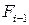меньшим, чем 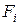, а второй – с сечением 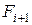большим, чем 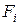. Допустим, что 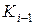< 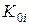, а 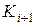> 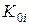. Тогда будут выполняться неравенства: 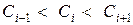и 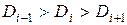, а соответствующие параболы займут положение, показанное на рис.4.2, кривые 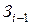и .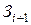

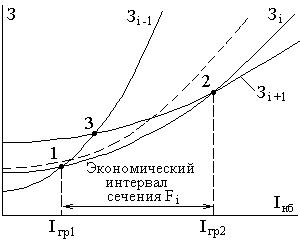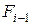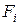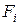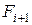Как видно из рис.4.2, в точках 1, 2 и 3 параболы пересекаются. Это значит, что при соответствующих этим точкам токах приведенные затраты на линию одинаковы для двух сечений. Так, например, в точке 1 равнозатратны варианты линии с сечениями и , а в точке 2 - варианты линии с сечениями и . Ток 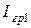, соответствующий точке 1, называется граничным, потому, что при токах меньших, чем этот, выгоднее сечение 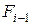_, а при токах, больших, чем этот выгоднее сечение .

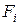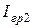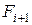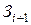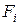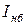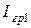Но, если ток в линии больше граничного тока , то выгоднее становится сечение , так как в этой области ниже всех проходит парабола . Таким образом, экономическим интервалом сечения (то есть интервалом, где это сечение самое выгодное) является интервал токов между и .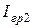

Аналогично, экономический интервал сечения 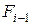находится левее тока 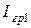, а экономический интервал сечения 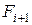, - правее тока 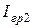(если не рассматривать варианты с другими сечениями).

Если рассмотреть варианты линии со всеми сечениями, применяе­мыми при данном номинальном напряжении, то вся область токов будет разбита на интервалы, в каждом из которых экономически целесообразным будет одно из сечений. При этом может оказаться, что для некоторых сечений кривая затрат на всем протяжении проходит выше остальных (пунктирная линия на рис.4.2). Это означает, что данное сечение своего экономического интервала не имеет, то есть невыгодно при любых токах.

Таким образом, для выбора экономически целесообразного сечения в принципе достаточно отложить на оси абсцисс ток, ожидаемый в проектируемой линии в часы наибольших нагрузок и посмотреть, в экономический интервал какого сечения он попадает. Однако на практике рассчитывать затраты и строить кривые по типу рис.4.2 было бы слишком трудоемко. Поэтому метод получил свое дальнейшее развитие, и в литературе [3,7] опубликованы таблицы граничных токов, а также номограммы для выбора экономически целесообразных сечений.

Чтобы грамотно пользоваться номограммами, рассмотрим, как они построены. Как следует из рис.4.2, при токе в линии, равном граничному, два смежных сечения равнозатратны, то есть справедливо равенство:

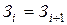; или ;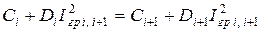

Отсюда можно получить выражение для граничного тока 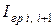между экономическими интервалами сечени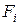й и : .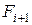

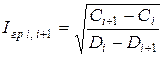Подставив в это выражение вместо коэффициентов C и D их значения из (4-4), после преобразований получим:

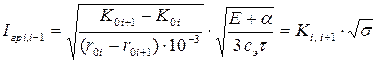; (4-7)

где 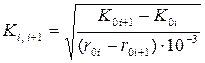, А/( руб./кВт)^1/2 - коэффициент, зависящий от стоимости сооружения одного километра линии, то есть от ее конструктивного исполнения (имеется в виду номинальное напряжение, материал опор, одноцепная или двухцепная, район по гололеду – все это сказывается на величине );

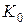и 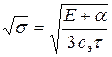, (кВт/руб)^1/2 ; - аргумент, зависящий от параметров, входящих в подкоренное выражение.

Номограммы представляют собой графики 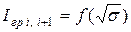, построенные для разных пар смежных сечений. Как следует из (4-7), они представляют собой пучок прямых линий, выходящих из начала координат (рис. 4.3). Секторы между ними и есть экономические интервалы применяемых сечений. Если для какого-либо сечения сектор отсутствует, то это значит, что данное сечение экономического интервала не имеет. Для каждого конструктивного исполнения линии имеется отдельная номограмма [3].

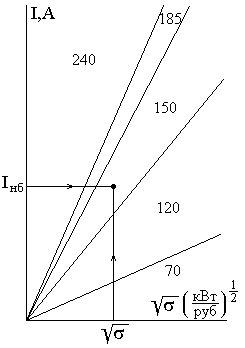Выбор экономически целесообраз­ного сечения по номограммам экономиче­ских интервалов производится в следую­щем порядке.

1.Выбирается номограмма, соответст­вующая принятому конструктив­ному исполнению линии.

2.Определяется величина параметра 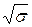и откладывается на оси абсцисс.

3.Определяется расчетное значение наибольшего тока в проектируемой линии 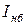и откладывается на оси ординат.

4.По точке пересечения полученных координат выбирается сечение.

При пользовании готовыми номограммами из справочников необходимо помнить, что они получены и опубликованы много лет назад. Стоимость сооружения линий (от которой зависит коэффициент 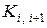) за прошедшее время сильно изменилась, поэтому наклон границ интервалов уже не соответствует действительности. Для приближенного учета этого фактора рекомендуется при определении параметра 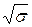ввести в него коэффициент удорожания, то есть пользоваться формулой:

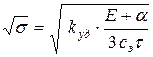; (4-8)

Более радикальным и более надежным решением будет построение собственных номограмм с использованием сегодняшних цен. Порядок построения таких номограмм рассмотрен ниже, в п. 4.7.1.