Определение наращенной суммы по простым и сложным процентам с использование различных схем начисления процентов.

ВАРИАНТ 9

Определение наращенной суммы по простым и сложным процентам с использование различных схем начисления процентов.

Задача 3.1.1. Определить наращенную сумму, если первоначальная сумма в размере 2000 р. была помещена на депозитный счет на период 0,5 лет под 30 % годовых. Наращение осуществляется по простой ссудной процентной ставке.

РЕШЕНИЕ.

К наращению по простым процентам обычно прибегают при выдаче краткосрочных ссуд (на срок до 1 года) или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются. Для записи формулы наращения простых процентов (simple interest) примем обозначения:

I — проценты за весь срок ссуды;

РV — первоначальная сумма долга;

FV — наращенная сумма, т. е. сумма в конце срока;

i — ставка наращения процентов (десятичная дробь);

n — срок ссуды.

Если срок измеряется в годах (как это обычно и бывает), то i означает годовую процентную ставку.

Соответственно каждый год приносит проценты в сумме: Pv×i.

Начисленные за весь срок проценты составят: I = PV×ni.

I = 2000*0,5*0,3=300 руб.

Наращенная сумма, таким образом, находится по формуле:

FV = РV + I = РV + PV×ni = РV(1 + ni).

FV=2000+300=2300 руб.

Ответ: Наращенная сумма составляет 2300 руб.

Задача 3.1.2. Определить наращенную сумму, которую необходимо проставить в бланке векселя, если ссуда выдается на 0,5 лет в размере 2000 р. Наращение осуществляется по простым процентам по учетной ставке ‒ 30 % годовых.

РЕШЕНИЕ.

Простая учетная ставка иногда применяется и при расчете наращенной суммы. Например, при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга:

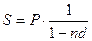
Множитель наращения: .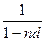

S=2000*1/(1-0,5*0,3)= 2353 руб.

Ответ: Наращенную сумму, которую необходимо проставить в бланке векселя равна 2353 руб.

Задача 3.1.3. Кредит в размере 2000 р. выдан с 22.03 по 14.11. включительно под 30% годовых. Год не високосный. Определить сумму, которую необходимо будет вернуть банку, используя точные проценты с точным числом дней ссуды, обыкновенные проценты с точным числом дней ссуды, обыкновенные проценты с приближенным числом дней ссуды.

РЕШЕНИЕ.

В нашем случае для годовой ставки i простых процентов наращенная сумма S:

S = P (1 + n∙i),

где 1 + n∙i — множитель наращения, а годовая ставка i простых процентов (rate of interest).

В нашем случае срок финансового соглашения n измеряется не в годах, а в днях t, то в (1) в качестве n следует взять, где K — так называемая временная база, т.е. число дней в году, K =360,365(366).

Если временная база K = 360 дней (12 месяцев по 30 дней), то говорят, что в формуле используют обыкновенные, или коммерческие проценты.

а) точные проценты с точным числом дней ссуды. Этот вариант
(K = 365(366)) дает самые точные результаты.

S = 2000*(1+0,3*238/365) =2391 руб.

б) обыкновенные проценты с точным числом дней ссуды. Этот метод (K = 360), иногда называемый банковским, распространен в ссудных операциях коммерческих банков. Он дает несколько больший результат, чем предыдущий метод.

S = 2000*(1+0,3*238/360) = 2397 руб.

в) обыкновенные проценты с приближенным числом дней ссуды:

S = 2000*(1+0,3*235/360) =2392 руб.

Ответ: 2391 руб., 2397 руб., 2393 руб.

Задача 3.1.4. Кредит в размере 2000 р. выдан 22.03 по 14.11 включительно под 30% годовых. Год не високосный. Определить сумму, которую необходимо будет вернуть банку, используя точные проценты с точным числом дней ссуды, обыкновенные проценты с точным числом дней ссуды, обыкновенные проценты с приближенным числом дней ссуды.

РЕШЕНИЕ.

При расчете обычно полагают, что К = 360 (12 месяцев по 30 дней) или К = 365, 366 дней. Если К = 360 дней, проценты называются обыкновенными. В этом случае формула примет вид:

.

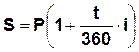При использовании действительной продолжительности года 365(366) получают точные проценты и в этом случае формула примет вид:

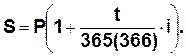
а) Точные проценты с точным числом дней ссуды:

S=2000*(1+238/365*0,3)= 2391 руб.

б) Обыкновенные проценты с точным числом дней ссуды:

S=2000*(1+238/360*0,3)=2397 руб.

в) Обыкновенные проценты с приближенным числом дней ссуды:

S=2000*(1+235/360*0,3)=2392 руб.

Ответ: 23945 руб., 2397 руб., 2393 руб.

Задача 3.1.5. Первоначальная сумма в размере 2000 р. была положена в банк на 4 года под 30 % годовых. Определить наращенную сумму по сложным процентам через 4 года.

РЕШЕНИЕ.

Наращенная сумма после 4 лет:

S = Р(1 + 1)ⁿ

S = 2000*(1 + 0,3)⁴ = 5712 руб.

Ответ: Наращенная сумма по сложным процентам составит 5712 руб.

Задача 3.1.6. Первоначальная сумма в размере 2000 р. была выдана в долг на 4 года. Определить наращенную сумму, которая должна быть возвращена через 4. года, если начисление процентов осуществляет по учетной ставке 30 % годовых.

РЕШЕНИЕ.

Наращенная сумма, которая должна быть возвращена через 4 года:

S = Р(1 + ni)

S=2000*(1+0,3*4)= 4400 руб.

Ответ: 4400 руб.

Задача 3.1.7. Первоначальная сумма в размере 2000 р. была положена на депозитный вклад 1 апреля на квартал под 30% годовых. Согласно условиям контракта предусмотрено ежедневное начисление простых процентов. Определить наращенную сумму, используя начисление точных процентов с точным числом дней ссуды, обыкновенных процентов с точным числом дней ссуды, обыкновенных процентов с приближенным числом дней ссуды.

РЕШЕНИЕ.

Простые проценты считаются по такой формуле:

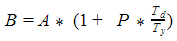, Где В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Td – срок вклада в днях, Ty– количество дней в году.

а) расчет наращенной суммы по точным процентам с точным числом дней ссуды:

В=2000*(1+0,3*90/365)=2148 руб.

б) Расчет обыкновенных процентов с точным числом дней ссуды:

В=2000*(1+0,3*90/360)=2150 руб.

в) расчет обыкновенных процентов с приближенным числом дней ссуды:

В=2000*(1+0,3*80/360)=2133 руб.

Ответ: 2148 руб., 2150 руб., 2133 руб.

Задача 3.1.8. Первоначальная сумма в размере 2000 р. была положена в банк на 4 года под 30 % годовых. Согласно контракту предусмотрено ежедневное начисление сложных процентов. Определить наращенную сумму через 4 года.

РЕШЕНИЕ.

Расчет сложных процентов производится по следующей формуле:

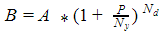, Где В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Ny– количество периодов капитализации в году, Nd – количество периодов капитализации за весь период вклада.

Для вкладов со сложным процентом важной часть является периодичность начисления процентов.

В=2000*(1+0,3/90)¹⁶=2109 руб.

Ответ: 2109 руб.

Задача 3.1.9. Контракт предусматривает следующий порядок начисления процентов: первый квартал ‒ 30 % годовых; в каждом следующем квартале ставка повышается на 0,4%. Определить наращенную сумму, если контракт подписан на одни год, а первоначальная сумма составляет 2000 р.

РЕШЕНИЕ.

При установлении переменной процентной ставки наращенная сумма определяется:

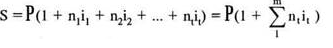
Выражение в скобках и представляет собой множитель наращения. Рассчитаем его:

1 + 1*0,3 + 0,4*0,34 + 0,4*0,38 + 0,4*0,42 = 1,756 раз

Таким образом, по данному контракту наращенная сумма будет в 1,756 раза больше первоначальной.

Рассчитаем наращенную сумму:

S=2000*1,756=3512 руб.

Ответ: 3512 руб.

Задача 3.1.10. Контракт подписан на 4 года и предусматривает следующий порядок начисления сложных процентов: 1 год ‒ 30 % годовых; в каждом последующем полугодии процентная ставка увеличивается на 0,05%. Определить наращенную сумму, если первоначальная сумма составляет 2000 р.

РЕШЕНИЕ.

При установлении переменной процентной ставки наращенная сумма определяется:

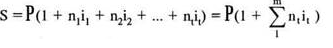
Выражение в скобках и представляет собой множитель наращения. Рассчитаем его:

1 + 1*0,3 + 0,5*0,35 + 0,5*0,4 + 0,5*0,45 =1,9 раз

Таким образом, по данному контракту наращенная сумма будет в 1,9 раза больше первоначальной.

Рассчитаем наращенную сумму:

S=2000*1,9=3800 руб.

Ответ: 3800 руб.

РЕШЕНИЕ.

Рассчитаем дисконтированный множитель:

d= 1/(1+r)n.

Рассчитаем дисконт по точным процентам с точным числом дней ссуды:

D=S*1/(1+r)n

D=200000*1/(1+0,3)*120/365=50580руб.

Рассчитаем дисконт по обыкновенным процентам с точным числом дней ссуды:

D=200000-200000*(1+0,3*120/365)= 19726 руб.

Ответ: 50580 руб., 19726 руб.

Задача 3.2.2. Определить сумму, которую необходимо положить в банк, чтобы при начислении на нее процентов по сложной процентной ставке – 30% годовых, получить через 3 года наращенную сумму в размере 200000 р., а также сумму дисконта.

РЕШЕНИЕ.

Дисконтирование по сложной учетной ставке осуществляется по формуле:

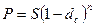
где d_c - сложная годовая учетная ставка.

Дисконт в этом случае равен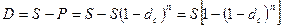

Р=200000*(1-0,3)³=68600 руб.

D=200000-68600=131400 руб.

Ответ: 131400 руб.

Задача 3.2.3. Вексель выдан на 200000 р. с уплатой 20.09. Владелец векселя учел его в банке 120 дней по учетной процентной ставке – 30 %. Определить сумму, которую получит держатель векселя, если начисление процентов осуществляется по точным процентам с точным числом дней ссуды, обыкновенным процентам с точным числом дней ссуды, обыкновенным процентам с приближенным числом дней ссуды, а также суммы дисконта.

РЕШЕНИЕ.

Учетная ставка рассчи­тывается отношением наращения (F-P) к ожидаемой в будущем к получению, или наращенной, величине F.

Определим сумму, которую получит держатель векселя по формулам:

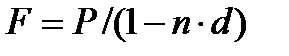
Где P- вложенная сумма (сумма, которую получает владелец векселя при его учете);

F – наращенная сумма (номинальная стоимость векселя);

n- количество периодов продолжительности финансовой операции;

d-простаяучетная ставка;

t -продолжительность финансовой операции в днях;

Т- количество дней в году.

а) если начисление процентов осуществляется по точным процентам с точным числом дней ссуды:

F=200000/(1-120/365*0,3)=221884 руб.

Сумма дисконта:

D=F-P

D=221884-200000=21884 руб.

б) если проценты начисляются обыкновенные с приближенным числом дней ссуды:

F=200000/(1-120/360*0,3)= 222222 руб.

Сумма дисконта:

D=222222-200000=22222 руб.

Ответ: 221884 руб., 21884 руб., 222222руб.,22222 руб.

Задача 3.2.4. Предприятие предоставило покупателю отсрочку платежа сроком на 3 года и учло платежное обязательство на сумму 200000 р. в банке по учетной ставке 30 % годовых. Определить сумму, которую получит на руки держатель платежного обязательства.

РЕШЕНИЕ.

Рассчитаем сумму, которую получит держатель платежного обязательства по формуле:

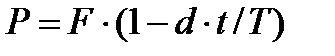
Где P- вложенная сумма (сумма, которую получает владелец векселя при его учете);

F – наращенная сумма (номинальная стоимость векселя);

n- количество периодов продолжительности финансовой операции;

d-простаяучетная ставка;

t -продолжительность финансовой операции в днях;

Т- количество дней в году.

Р=200000*(1-0,3*3*365/365)=20000 руб.

Ответ: 20000 руб.

РЕШЕНИЕ.

При выборе вида вклада, на порядок начисления процентов стоит обращать внимание. Когда сумма вклада и срок размещения значительные, а банком применяется формула простых процентов, это приводит к занижению суммы процентного дохода вкладчика. Формула простых процентов по вкладам выглядит так:

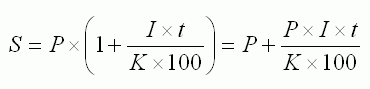
Где S — сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита. Она состоит из первоначальной суммы размещенных денежных средств, плюс начисленные проценты;

I – годовая процентная ставка;

t – количество дней начисления процентов по привлеченному вкладу;

K – количество дней в календарном году (365 или 366);

P – первоначальная сумма привлеченных в депозит денежных средств.

Рассчитаем количество дней начисления процентов:

50000=2000+(2000*0,3t)

48000=2000*0,3t

24=0,3t

t=24/0,3

t=80 дней.

Ответ:80 дней.

Задача 3.3.2. Предприятие планирует получить наращенную сумму в размере 50000 р. На какой срок необходимо вложить первоначальную сумму 2000 р. под 30 % годовых, чтобы получить требуемую наращенную сумму.

РЕШЕНИЕ.

Формула для расчета наращенной суммы вклада по методу простых процентов имеет вид:

К_н=К_о*(1+р*n),

Где К_н-наращенная сумма по вкладу;

К_о-первоначальная сумма вклада;

р-проценты по вкладу;

n- количество лет начисления процентов.

Рассчитаем количество лет начисления процентов:

50000=2000*(1+0,3*n)

50000=2000+600n

48000=600n

n=80 дней

Ответ: 80 дней

Задача 3.3.3. Первоначальная сумма в размере 2000 р. будет вложена на депозитный счет под 30 % годовых. Определить через какой срок наращенная стоимость этой первоначальной суммы составит 50000 р.

РЕШЕНИЕ.

Наращенная сумма рассчитывается используя формулу:

I=P*i*d,

где Р – сумма вклада;

i – процентная ставка;

d – количество дней.

Рассчитаем срок вклада:

50000=2000*0,3*d

d=83 дня

Ответ: 83 дня.

Задача 3.3.4. Предприятие планирует получить наращенную сумму в размере 50000 р. На какой срок необходимо вложить первоначальную сумму 2000 р. под 30 % годовых, чтобы получить требуемую наращенную сумму.

РЕШЕНИЕ.

Определим доход:

I = S - P

I= 50000 – 2000=48000руб.

S - наращенный капитал

P - первоначальный капитал

Теперь определим срок вклада:

d=100*48000/(30*2000)=80 дней

Ответ: 80 дней.

3.4. Определение наращенной и дисконтированной стоимости финансовой ренты (аннуитета).

Задача 3.4.1. Предприятие с целью создания страхового фонда на счет в банке вносит в конце каждого года платеж в размере 2000 р. в течение 4 лет. Определить наращенную сумму на счете через 4 года, если годовая ссудная процентная ставка – 30 %.

РЕШЕНИЕ.

Расчет наращенной суммы выполним по формуле:

F = P*(1 + n * d)

F =2000*(1+0,3*4*365/365) =4400 руб.

Ответ: 4400 руб.

Задача 3.4.2. Предприятие с целью создания страхового фонда на счет в банке вносит в начале каждого года 2000 р. в течение 4 лет. Определить наращенную сумму на счете через 4года, если годовая ссудная процентная ставка – 30 %.

РЕШЕНИЕ.

Вычисления произведем по следующей формуле:

S = P (1+in),

где S – наращенная стоимость кредита;

P – настоящая стоимость кредита;

i – годовая процентная ставка;

n – период начисления процентов в годах.

S = 2000* (1 + 0,3 * 3*365/365) = 3800 руб.

Ответ: 3800 руб.

Задача 3.4.3.Страховая компания заключает договор с предприятием на 4 года. Страховые взносы предприятия в размере 2000 р. страховая компания помещает в банк под 30% годовых с полугодовой капитализацией. Определить сумму, которую получит страховая компания.

РЕШЕНИЕ.

Вычисления произведем по следующей формуле:

S = P (1+in),

где S – наращенная стоимость кредита;

P – настоящая стоимость кредита;

i – годовая процентная ставка;

n – период начисления процентов в годах.

S = 2000* (1 + 0,3 * 0,5*4*365/365) = 3200 руб.

Ответ: 3200 руб.

Задача 3.4.4. Предприятия в течение трех лет вносит в банк в конце каждого года платеж в размере 2000 р. Проценты на вклад начисляются по сложной годовой процентной ставке равной 30 %. Определить дисконтированную стоимость аннуитета.

РЕШЕНИЕ.

Таким образом, в общем виде формула наращенной суммы может быть записана в виде:

S = P* ,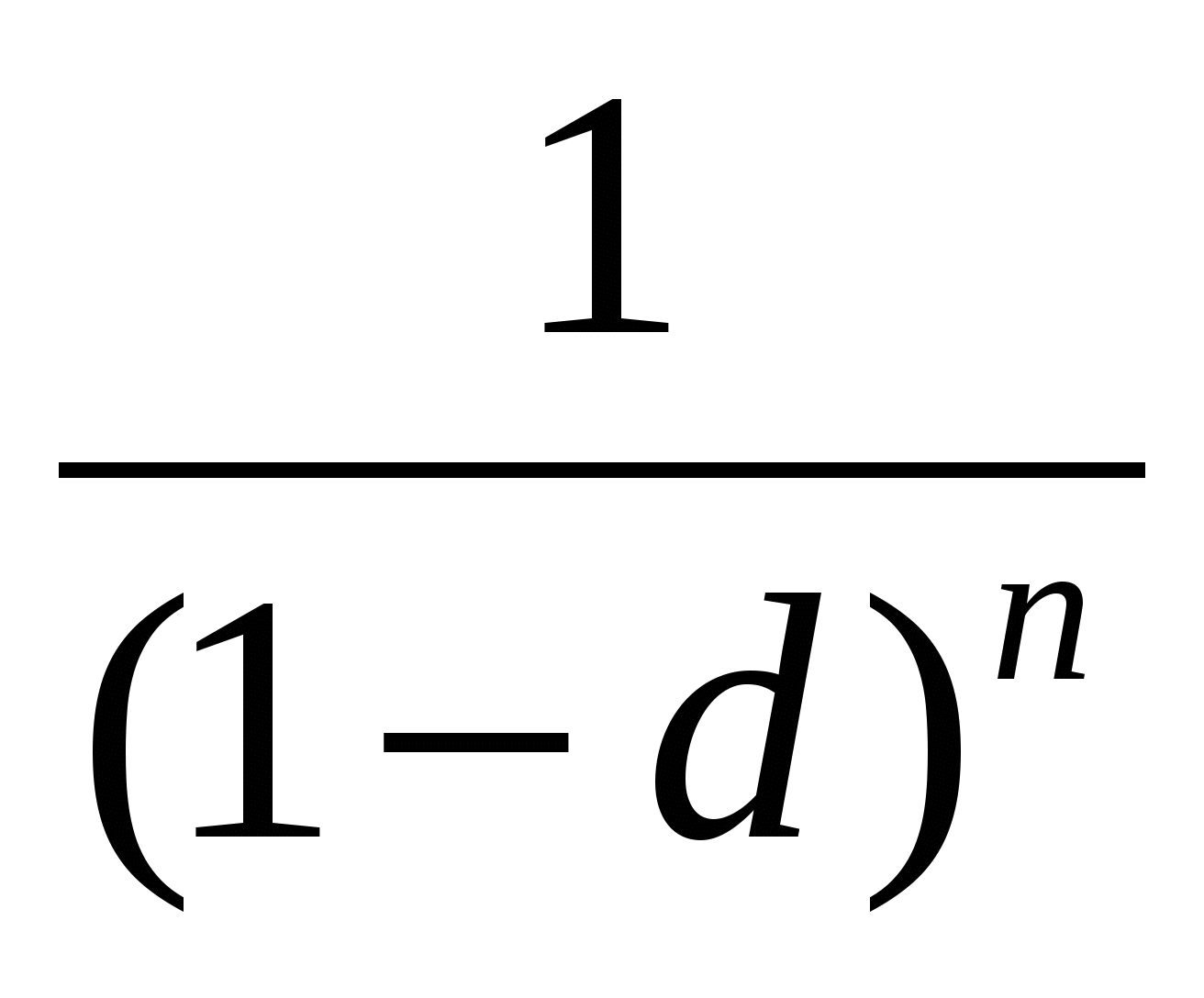

где 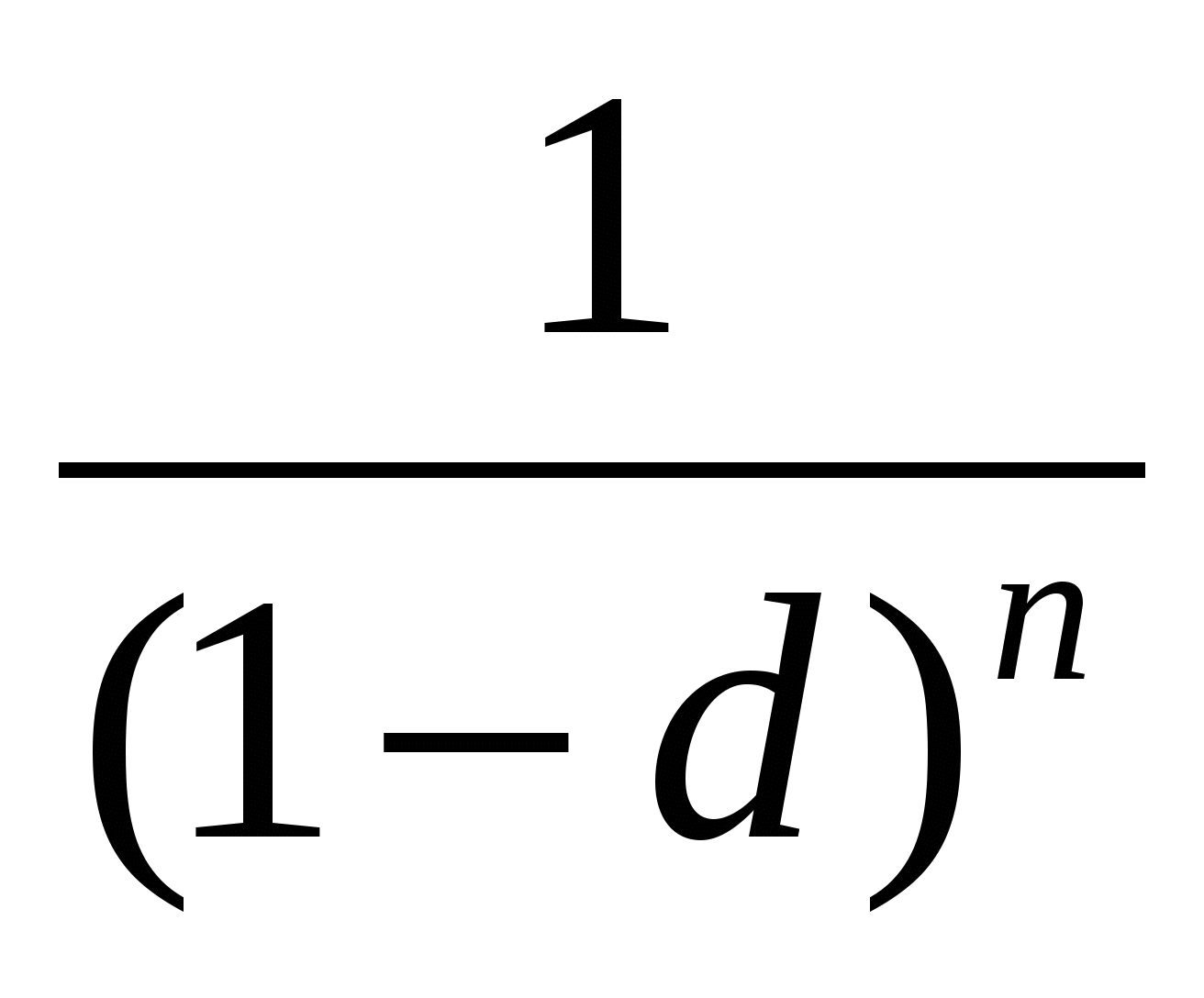- коэффициент наращения при вычислении сложных процентов;

d – учетная ставка сложных процентов;

n – число лет.

Рассчитаем наращенную сумму:

S=2000*(1/(1-0,3)³)= 5831 руб.

Дисконтированная сумма равна:

D=S-P

D=5831-2000=3831 руб.

Ответ: 3831 руб.

Задача 3.4.5. Предприятия в течение трех лет вносит в банк в начале каждого года платеж в размере 2000 р. Проценты на вклад начисляются по сложной годовой процентной ставке равной 30 %. Определить дисконтированную стоимость аннуитета.

РЕШЕНИЕ.

Таким образом, в общем виде формула наращенной суммы может быть записана в виде:

S = P* ,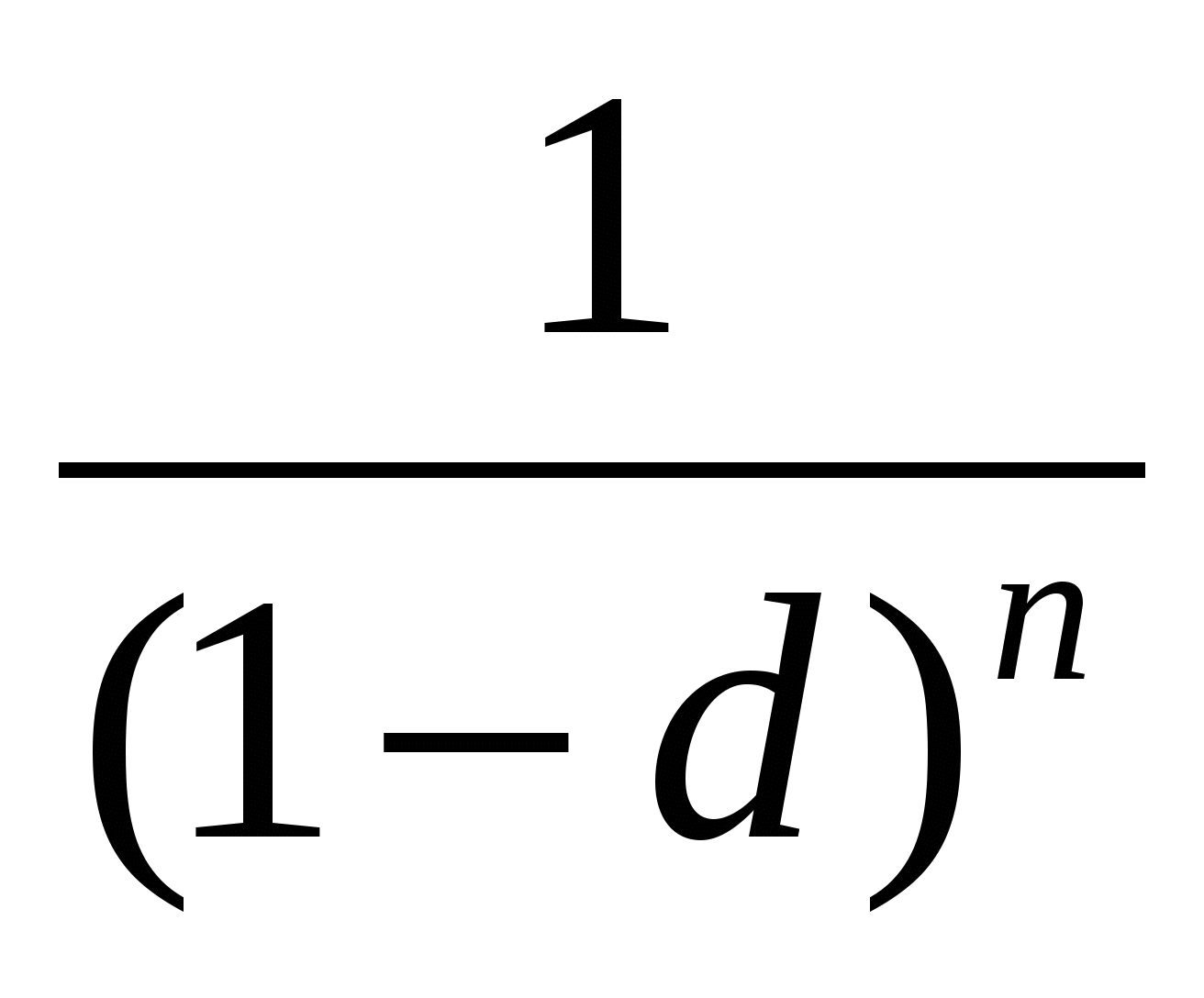

где 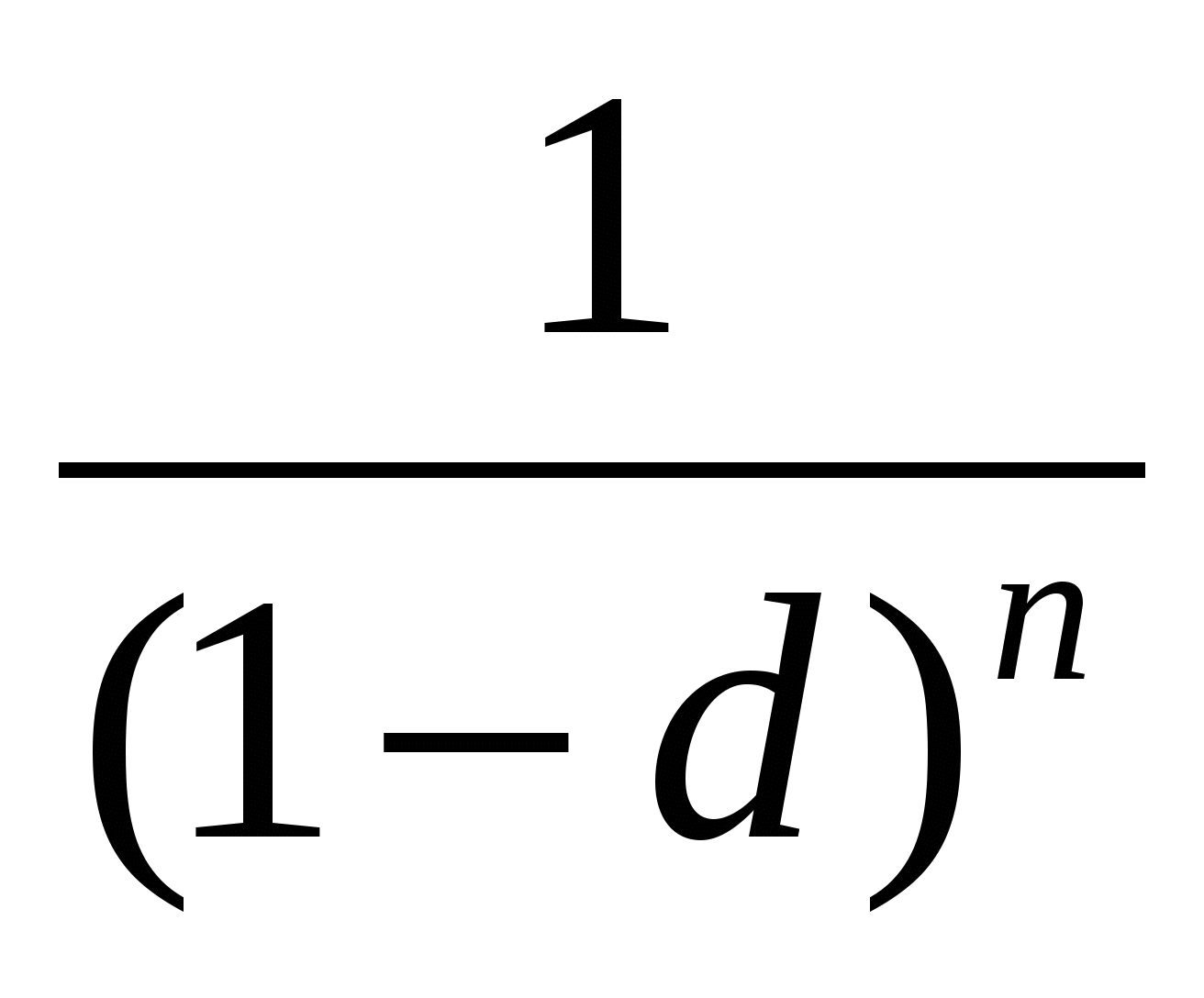- коэффициент наращения при вычислении сложных процентов;

d – учетная ставка сложных процентов;

n – число лет.

Рассчитаем наращенную сумму:

S=2000*(1/(1-0,3)²)= 4082 руб.

Дисконтированная сумма равна:

D=S-P

D=4082-2000=2082 руб.

Ответ: 2082 руб.

РЕШЕНИЕ.

Рассмотрим планирование фонда с постоянными срочными взносами. Предположим, что создание погасительного фонда производится путем внесения в банк ежегодных взносов R, на которые начисляются проценты по ставке i. Одновременно про­исходит начисление процентов на величину долга по ставке g. При начислении на величи­ну долга простых процентов срочная уплата будет равна:

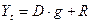
где 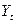-срочная уплата в период t;

D- величина долга.

При начислении на величину долга сложных процентов срочная уплата рассчитывается по формуле:

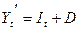
где 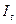- процентный платеж, исчисленный по сложным процентам.

Величину 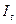для расчетного периода 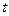вычисляют по формуле:

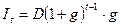
где ;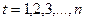

g - процентная ставка, начисляемая на основной долг.

Подставив значение 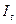получим:

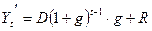
200000=(1+0,26)²*0,26/R

200000=1,58*0,26/R

0,26/R=126582 руб.

R=32911руб.

Ответ: 32911 руб.

Задача 3.5.6. Определить размер ежегодного платежа, вносимого в начале года в течение трех лет, для формирования страхового фонда в размере 200000 р., если размер сложной процентной ставки – 30 %.

РЕШЕНИЕ.

200000=(1+0,3)³*0,3/R

200000=2,197*0,3/R

200000=0,6591/R

R=131820 руб.

Ответ: 131820 руб.

Задача 3.5.7. Кредит взят на сумму 2000 р. сроком на 4 года под 30 % годовых. Определить размер ежегодных погасительных платежей, осуществляемых в конце года.

РЕШЕНИЕ.

Размер ежегодных погасительных платежей:

R=Ai/(1-1/(1+i)ⁿ)

R =2000*0,3/(1-1/(1+0,3)⁴)=924 руб.

Ответ: 924 руб.

Задача 3.5.8. Кредит взят на сумму 2000 р. сроком на 4 года под 30 % годовых. Определить размер ежегодных погасительных платежей, осуществляемых в начале года.

РЕШЕНИЕ.

Размер ежегодных погасительных платежей:

R=Ai/(1-1/(1+i)ⁿ)

R =2000*0,3/(1-1/(1+0,3)³)=1101 руб.

Ответ: 1101 руб.

Задача 3.5.9. Предприятие ежегодно в конце года вкладывает 20000 р. для формирования инвестиционного фонда. Процентная ставка – 30 % годовых. Определить срок финансовой ренты, по окончании которой наращенная сумма составит 1000000 р.

РЕШЕНИЕ.

1000000=20000*(1+0,3*n)

50=1,3n

n=38 дней

Ответ: 38 дней.

Задача 3.5.10 Предприятие ежегодно в начале года вкладывает 20000 р. для формирования инвестиционного фонда. Ссудная процентная ставка – 30 % годовых. Определить срок финансовой ренты, по окончании которой наращенная сумма составит 1000000 р.

РЕШЕНИЕ.

1000000=20000*(1+0,3*(n-1))

50=1,3(n-1)

n-1=38 дней

n=37 дней

Ответ: 37дней.

Задача 3.5.11. Предприятие планирует взять кредит в размере 1000000 р. под годовую процентную ставку равную 30 %. Ежегодный платеж в конце года составит 20000 р. Определить срок финансовой ренты, по окончании которой будет возвращена вся сумма кредита.

РЕШЕНИЕ.

Поскольку проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо- это обычная рента. Сумма всех взносов с начисленными процентами будет равна:

FVA=R*((1+i*n)-1)/i

1000000=20000*((1+0,3*n)-1)/0,3

50=0,3n/0,3

n=50 дней.

Ответ: 50 дней.

ВАРИАНТ 9

Определение наращенной суммы по простым и сложным процентам с использование различных схем начисления процентов.

Задача 3.1.1. Определить наращенную сумму, если первоначальная сумма в размере 2000 р. была помещена на депозитный счет на период 0,5 лет под 30 % годовых. Наращение осуществляется по простой ссудной процентной ставке.

РЕШЕНИЕ.

К наращению по простым процентам обычно прибегают при выдаче краткосрочных ссуд (на срок до 1 года) или в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются. Для записи формулы наращения простых процентов (simple interest) примем обозначения:

I — проценты за весь срок ссуды;

РV — первоначальная сумма долга;

FV — наращенная сумма, т. е. сумма в конце срока;

i — ставка наращения процентов (десятичная дробь);

n — срок ссуды.

Если срок измеряется в годах (как это обычно и бывает), то i означает годовую процентную ставку.

Соответственно каждый год приносит проценты в сумме: Pv×i.

Начисленные за весь срок проценты составят: I = PV×ni.

I = 2000*0,5*0,3=300 руб.

Наращенная сумма, таким образом, находится по формуле:

FV = РV + I = РV + PV×ni = РV(1 + ni).

FV=2000+300=2300 руб.

Ответ: Наращенная сумма составляет 2300 руб.

Задача 3.1.2. Определить наращенную сумму, которую необходимо проставить в бланке векселя, если ссуда выдается на 0,5 лет в размере 2000 р. Наращение осуществляется по простым процентам по учетной ставке ‒ 30 % годовых.

РЕШЕНИЕ.

Простая учетная ставка иногда применяется и при расчете наращенной суммы. Например, при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга:

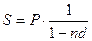
Множитель наращения: .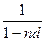

S=2000*1/(1-0,5*0,3)= 2353 руб.

Ответ: Наращенную сумму, которую необходимо проставить в бланке векселя равна 2353 руб.

Задача 3.1.3. Кредит в размере 2000 р. выдан с 22.03 по 14.11. включительно под 30% годовых. Год не високосный. Определить сумму, которую необходимо будет вернуть банку, используя точные проценты с точным числом дней ссуды, обыкновенные проценты с точным числом дней ссуды, обыкновенные проценты с приближенным числом дней ссуды.

РЕШЕНИЕ.

В нашем случае для годовой ставки i простых процентов наращенная сумма S:

S = P (1 + n∙i),

где 1 + n∙i — множитель наращения, а годовая ставка i простых процентов (rate of interest).

В нашем случае срок финансового соглашения n измеряется не в годах, а в днях t, то в (1) в качестве n следует взять, где K — так называемая временная база, т.е. число дней в году, K =360,365(366).

Если временная база K = 360 дней (12 месяцев по 30 дней), то говорят, что в формуле используют обыкновенные, или коммерческие проценты.

а) точные проценты с точным числом дней ссуды. Этот вариант
(K = 365(366)) дает самые точные результаты.

S = 2000*(1+0,3*238/365) =2391 руб.

б) обыкновенные проценты с точным числом дней ссуды. Этот метод (K = 360), иногда называемый банковским, распространен в ссудных операциях коммерческих банков. Он дает несколько больший результат, чем предыдущий метод.

S = 2000*(1+0,3*238/360) = 2397 руб.

в) обыкновенные проценты с приближенным числом дней ссуды:

S = 2000*(1+0,3*235/360) =2392 руб.

Ответ: 2391 руб., 2397 руб., 2393 руб.

Задача 3.1.4. Кредит в размере 2000 р. выдан 22.03 по 14.11 включительно под 30% годовых. Год не високосный. Определить сумму, которую необходимо будет вернуть банку, используя точные проценты с точным числом дней ссуды, обыкновенные проценты с точным числом дней ссуды, обыкновенные проценты с приближенным числом дней ссуды.

РЕШЕНИЕ.

При расчете обычно полагают, что К = 360 (12 месяцев по 30 дней) или К = 365, 366 дней. Если К = 360 дней, проценты называются обыкновенными. В этом случае формула примет вид:

.

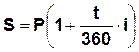При использовании действительной продолжительности года 365(366) получают точные проценты и в этом случае формула примет вид:

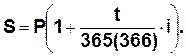
а) Точные проценты с точным числом дней ссуды:

S=2000*(1+238/365*0,3)= 2391 руб.

б) Обыкновенные проценты с точным числом дней ссуды:

S=2000*(1+238/360*0,3)=2397 руб.

в) Обыкновенные проценты с приближенным числом дней ссуды:

S=2000*(1+235/360*0,3)=2392 руб.

Ответ: 23945 руб., 2397 руб., 2393 руб.

Задача 3.1.5. Первоначальная сумма в размере 2000 р. была положена в банк на 4 года под 30 % годовых. Определить наращенную сумму по сложным процентам через 4 года.

РЕШЕНИЕ.

Наращенная сумма после 4 лет:

S = Р(1 + 1)ⁿ

S = 2000*(1 + 0,3)⁴ = 5712 руб.

Ответ: Наращенная сумма по сложным процентам составит 5712 руб.

Задача 3.1.6. Первоначальная сумма в размере 2000 р. была выдана в долг на 4 года. Определить наращенную сумму, которая должна быть возвращена через 4. года, если начисление процентов осуществляет по учетной ставке 30 % годовых.

РЕШЕНИЕ.

Наращенная сумма, которая должна быть возвращена через 4 года:

S = Р(1 + ni)

S=2000*(1+0,3*4)= 4400 руб.

Ответ: 4400 руб.

Задача 3.1.7. Первоначальная сумма в размере 2000 р. была положена на депозитный вклад 1 апреля на квартал под 30% годовых. Согласно условиям контракта предусмотрено ежедневное начисление простых процентов. Определить наращенную сумму, используя начисление точных процентов с точным числом дней ссуды, обыкновенных процентов с точным числом дней ссуды, обыкновенных процентов с приближенным числом дней ссуды.

РЕШЕНИЕ.

Простые проценты считаются по такой формуле:

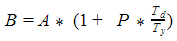, Где В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Td – срок вклада в днях, Ty– количество дней в году.

а) расчет наращенной суммы по точным процентам с точным числом дней ссуды:

В=2000*(1+0,3*90/365)=2148 руб.

б) Расчет обыкновенных процентов с точным числом дней ссуды:

В=2000*(1+0,3*90/360)=2150 руб.

в) расчет обыкновенных процентов с приближенным числом дней ссуды:

В=2000*(1+0,3*80/360)=2133 руб.

Ответ: 2148 руб., 2150 руб., 2133 руб.

Задача 3.1.8. Первоначальная сумма в размере 2000 р. была положена в банк на 4 года под 30 % годовых. Согласно контракту предусмотрено ежедневное начисление сложных процентов. Определить наращенную сумму через 4 года.

РЕШЕНИЕ.

Расчет сложных процентов производится по следующей формуле:

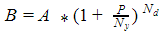, Где В – итоговая сумма, А – первоначальная сумма вклада, Р – годовая процентная ставка, Ny– количество периодов капитализации в году, Nd – количество периодов капитализации за весь период вклада.

Для вкладов со сложным процентом важной часть является периодичность начисления процентов.

В=2000*(1+0,3/90)¹⁶=2109 руб.

Ответ: 2109 руб.

Задача 3.1.9. Контракт предусматривает следующий порядок начисления процентов: первый квартал ‒ 30 % годовых; в каждом следующем квартале ставка повышается на 0,4%. Определить наращенную сумму, если контракт подписан на одни год, а первоначальная сумма составляет 2000 р.

РЕШЕНИЕ.

При установлении переменной процентной ставки наращенная сумма определяется:

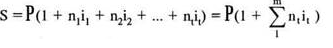
Выражение в скобках и представляет собой множитель наращения. Рассчитаем его:

1 + 1*0,3 + 0,4*0,34 + 0,4*0,38 + 0,4*0,42 = 1,756 раз

Таким образом, по данному контракту наращенная сумма будет в 1,756 раза больше первоначальной.

Рассчитаем наращенную сумму:

S=2000*1,756=3512 руб.

Ответ: 3512 руб.

Задача 3.1.10. Контракт подписан на 4 года и предусматривает следующий порядок начисления сложных процентов: 1 год ‒ 30 % годовых; в каждом последующем полугодии процентная ставка увеличивается на 0,05%. Определить наращенную сумму, если первоначальная сумма составляет 2000 р.

РЕШЕНИЕ.

При установлении переменной процентной ставки наращенная сумма определяется:

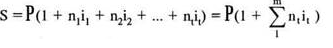
Выражение в скобках и представляет собой множитель наращения. Рассчитаем его:

1 + 1*0,3 + 0,5*0,35 + 0,5*0,4 + 0,5*0,45 =1,9 раз

Таким образом, по данному контракту наращенная сумма будет в 1,9 раза больше первоначальной.

Рассчитаем наращенную сумму:

S=2000*1,9=3800 руб.

Ответ: 3800 руб.