Сложные проценты, определение наращенной суммы при внутригодовой капитализации.

Основной областью применения простой процентной и учетной ставок являются краткосрочные финансовые операции, длительность которых менее 1 года. Вычисления с простыми ставками не учитывают возможность реинвестирования начисленных процентов, потому что наращение и дисконтирование производятся относительно неизменной исходной суммы P или S. В отличие от них сложные ставки процентов учитывают возможность реинвестирования процентов, так как в этом случае наращение производится по формуле не арифметической, а геометрической прогрессии, первым членом которой является начальная сумма P, а знаменатель равен (1 + i).

P, P * (1 + i), P * (1 + i)², P * (1 + i)³ , …, P * (1 + i)ⁿ,

где число лет ссуды n меньше числа членов прогрессии k на 1 (n = k – 1).

Наращенная стоимость (последний член прогрессии) находится по формуле: S=P 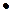(1+i)ⁿ

где (1 + i) ⁿ – множитель наращения декурсивных сложных процентов.

С позиций финансового менеджмента использование сложных процентов является более предпочтительным, т.к. признание возможности собственника в любой момент инвестировать свои средства с целью получения дохода является краеугольным камнем всей финансовой теории. При использовании простых процентов эта возможность часто не учитывается, поэтому результаты вычислений получаются менее корректными. При длительности операций менее 1 года (n < 1) начисление простых процентов обеспечивает получение результатов даже более выгодных для кредитора, чем использование сложных процентов. Сама по себе сложная процентная ставка i ничем не отличается от простой и рассчитывается по такой же формуле. Сложная учетная ставка определяется по формуле: d=D/P=(S-P)/S

Так же как и в случае простых процентов возможно применение сложной учетной ставки для начисления процентов (антисипативный метод):

S=P/(1-d)ⁿ,

где 1/(1-d)ⁿ – множитель наращения сложных антисипативных процентов.

Однако практическое применение такого способа наращения процентов весьма ограничено.

Важной особенностью сложных процентов является зависимость конечного результата от количества начислений в течение года. Здесь опять сказывается влияние реинвестирования начисленных процентов: база начисления возрастает с каждым новым начислением, а не остается неизменной, как в случае простых процентов . Например, если начислять 20% годовых 1 раз в год, то первоначальная сумма в 1 тыс. рублей возрастет к концу года до 1,2 тыс. рублей (1 * (1+ 0,2)). Если же начислять по 10% каждые полгода, то будущая стоимость составит 1,21 тыс. рублей (1 * (1 + 0,1) * (1 + 0,1)), при поквартальном начислении по 5% она возрастет до 1,216 тыс. рублей. По мере увеличения числа начислений (m) и продолжительности операции эта разница будет очень сильно увеличиваться. Если разделить сумму начисленных процентов при ежеквартальном наращении на первоначальную сумму, то получится 21,6% (0,216 / 1 * 100), а не 20%. Следовательно, сложная ставка 20% при однократном наращении и 20% (четыре раза по 5%) при поквартальном наращении приводят к различным результатам, то есть они не являются эквивалентными. Цифра 20% отражает уже не действительную (эффективную), а номинальную ставку. Эффективной процентной ставкой является значение 21,6%. В финансовых расчетах номинальную сложную процентную ставку принято обозначать буквой j. Формула наращения по сложным процентам при начислении их m раз в году имеет вид:

S=P(1+j/m)^mn

Пример 7. ссуда размером 5 млн. рублей выдана на 2 года по номинальной сложной процентной ставке 35% годовых с начислением процентов 2 раза в год. Будущая сумма к концу срока ссуды составит:

S = 5 * (1 + 0,35 / 2) ^{(2 * 2)} = 9,531 млн. рублей.

При однократном начислении ее величина составила бы лишь 9,113 млн. рублей 5 * (1 + 0,35)^2; зато при ежемесячном начислении возвращать пришлось бы уже 9,968 млн. рублей (5 * (1 + 0,35 / 12)^(12 * 2).

При начислении антисипативных сложных процентов, номинальная учетная ставка обозначается буквой f, а формула наращения принимает вид:

S=P/(1- f/m)^mn.

Выражение 1 / (1 – f / m)^mn множитель наращения по номинальной учетной ставке.

Дисконтирование по сложным процентам также может выполняться двумя способами – математическое дисконтирование и банковский учет. Последний менее выгоден для кредитора, чем учет по простой учетной ставке, поэтому используется крайне редко. В случае однократного начисления процентов его формула имеет вид:

P=S(1- d)ⁿ,

где (1 –d)ⁿ – дисконтный множитель банковского учета по сложной учетной ставке.

при m > 1 получаем:

P=S(1- f / m)^mn,

где f – номинальная сложная учетная ставка,

(1 – f / m)^mn – дисконтный множитель банковского учета по сложной номинальной учетной ставке.

Значительно более широкое распространение имеет математическое дисконтирование по сложной процентной ставке i. При неоднократном начислении процентов в течение года формула математического дисконтирования имеет вид:

P=S/(1+j / m)^mn

где j –номинальная сложная процентная ставка,

1/(1 + j / m)^mn – дисконтный множитель математического дисконтирования по сложной номинальной процентной ставке.

Пример 8, требуется определить современную стоимость платежа в размере 3 млн. рублей, который должен поступить через 1,5 года, процентная ставка составляет 40%:

при m = 1 P = 3 / (1 + 0,4)^1,5 = 1,811 млн. рублей

при m = 2 (начисление 1 раз в полугодие) P = (3 / (1 + 0,4 / 2)^{(2 * 1,5)} = 1,736 млн. рублей

при m = 12 (ежемесячное начисление) P = (3 / (1 + 0,4 / 12)^{(12 * 1,5)} = 1,663 млн. рублей.

По мере увеличения числа начислений процентов в течение года (m) промежуток времени между двумя смежными начислениями уменьшается – при m = 1 этот промежуток равен 1 году, а при m = 12 – только 1 месяцу. Теоретически можно представить ситуацию, когда начисление сложных процентов производится настолько часто, что общее его число в году стремится к бесконечности, тогда величина промежутка между отдельными начислениями будет приближаться к нулю, то есть начисление станет практически непрерывным. Такая на первый взгляд гипотетическая ситуация имеет важное значение для финансов и при построении сложных аналитических моделей (например при разработке масштабных инвестиционных проектов) часто применяют непрерывные проценты. Непрерывная процентная ставка обозначается буквой δ (читается “дельта”), часто этот показатель называют “сила роста”. Формула наращения по непрерывной процентной ставке имеет вид:

S=Pe ^δn

где e – основание натурального логарифма (≈2,71828...),

e ^δn – множитель наращения непрерывных процентов.

Например, чему будет равна через 3 года сумма 250 тыс. рублей, если сегодня положить ее на банковский депозит под 15% годовых, начисляемых непрерывно?

S = 250 * e^{(0,15 * 3)} = 392,1 тыс. рублей.

Для непрерывных процентов не существует различий между процентной и учетной ставками – сила роста является универсальным показателем. Однако, наряду с постоянной силой роста может использоваться переменная процентная ставка, величина которой меняется по заданному закону (математической функции). В этом случае можно строить очень мощные имитационные модели, однако математический аппарат расчета таких моделей достаточно сложен и не рассматривается в настоящем пособии, так же как и начисление процентов по переменной непрерывной процентной ставке.

Непрерывное дисконтирование с использованием постоянной силы роста выполняется по формуле:

P=S / e ^δn,

где 1 / e ^δn– дисконтный множитель дисконтирования по силе роста.

Пример 9.В результате осуществления инвестиционного проекта планируется получить через 2 года доход в размере 15 млн. рублей. Чему будет равна приведенная стоимость этих денег в сегодняшних условиях, если сила роста составляет 22% годовых?

P = 15 / e^{(0,22 * 2)} = 9,66 млн. рублей.

2.10 Тестовые задания

2011213. При многократном начислении сложных процентов начисление делается:

1.По отношению к конечной сумме предполагаемой к выплате;

2.По отношению к сумме с уже начисленными ранее процентами;

3.По отношению к средней сумме на начало и конец периода;

4.По отношению к сумме взятой в кредит.

2022132. Реальная процентная ставка – это процентная ставка:

1. Очищенная от процента;

2. Очищенная от нормы процента;

3. Очищенная от инфляции;

4. Очищенная от срока начисления процента.

2033214. Присоединение начисленной суммы процентов к сумме долга, которое служит базой для их начисления, называется:

1. Реализацией долга;

2. Реставрацией долга;

3. Детализацией долга;

4. Капитализацией долга;

5. Формализацией долга.

2041321. При долгосрочных ссудах наращенная сумма, рассчитанная по сложным процентам;

1.Значительно ниже, чем по простым процентам;

2.Одинакова с начислением по простым процентам;

3.Значительно выше, чем по простым процентам;

4.Нет правильного ответа.

2052214. Если начисление процентов проводится m раз в году, а срок долга n лет, то общее количество периодов начисления за весь срок финансовой операции будет осуществляться:

1. m 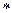n раз;

2. m+n раз;

3. (m+1) 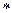n раз;

4. m 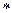(n+1) раз.

2063432. Ставка, которая показывает, какая годовая ставка сложных процентов дает тот же результат, что и m-разовое наращение год по ставке называется:

1. Реальной ставкой;

2. Эффективной ставкой;

3. Ставкой процента;

4. Множественной ставкой.