Прогнозирование на основе стандартных теоретических и эконометрических моделей поведения экономических агентов, развития экономических процессов и явлений, на микро- и макроуровне
В экономике исследуются теоретические модели, основанные на определенных формальных предпосылках (линейность, выпуклость, монотонность зависимостей, конкретные формулы взаимосвязи величин). Эконометрика занимается статистической оценкой моделей на основе изучения эмпирических данных. Изучение экономических процессов (взаимосвязей) в эконометрике осуществляется через эконометрические модели.
Применение эконометрики в экономике позволяет строить экономические модели и оценивать их параметры, проверять гипотезы о свойствах экономических показателей и формах их связи, что, в конечном счете, служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений. Любое эконометрическое исследование всегда предполагает объединение теории (экономической модели) и практики (статистических данных). Основная задача эконометрики - проверка экономических теорий на фактическом (эмпирическом) материале при помощи методов математической статистики. Теоретические модели используются для описания и объяснения наблюдаемых процессов на основе собранных статистических данных, с целью построения и обоснования моделей.
Теоретическая модель позволяет изучать общие свойства экономики и её характерных элементов дедукцией (от общего к частному) выводов из формальных предпосылок.
Эконометрическая модель - это математическое описание какого-либо экономического процесса или объекта.
Эконометрические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемых объектов, цели моделирования и используемого инструментария:
· Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупнённые материальные и финансовые показатели (ВВП, потребление, инвестиции, занятость, процентную ставку…).
· Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей в рыночной среде.
Основные этапы эконометрического исследования:
1. Постановочный этап - постановка проблемы, целей моделирования, сбор данных, анализ их качества.
2. Спецификация модели - выбор вида формулы зависимости.
3. Параметризация - оценка значений параметров выбранной модели.
4. Верификация - проверка качества полученных параметров и самой модели в целом.
5. Использование построенной модели для объяснения поведения экономических показателей и прогнозирования.
Различают точечное прогнозирование и интервальное.
Точечный прогноз – это число, значение зависимой переменной, вычисляемое для заданных значений независимых переменных. Интервальный прогноз – это интервал, в котором с заданным уровнем значимости (с заданной вероятностью) находится истинное значение зависимой переменной для заданных значений независимых переменных.
Выделяют три основных класса эконометрических моделей:
1) модель временных рядов;
2) модели регрессии с одним уравнением;
3) системы одновременных уравнений.
Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.
Моделью регрессии с одним уравнением называется зависимость результативной переменной, обозначаемой как у, от факторных (независимых) переменных, обозначаемых как х1,х2,…,хn. Данную зависимость можно представить в виде функции регрессии или модели регрессии.
Системой одновременных уравнений называется модель, которая описывается системами взаимозависимых регрессионных уравнений.
Системы одновременных уравнений могут включать в себя тождества и регрессионные уравнения, в каждое из которых могут входить не только факторные переменные, но и результативные переменные из других уравнений системы.
Интерпретацию результатов исследования приведем на примере линейной регрессии.
Парная регрессия представляет зависимость результативного признака только от одного факторного признака. Подбор типа функции для построения выборочного уравнения регрессии в случае парной регрессии чаще всего осуществляется на основе графического представления выборочных данных.
Модель имеет вид:  y=a+bx+ε где, y-зависимая переменная (результативный признак);
y=a+bx+ε где, y-зависимая переменная (результативный признак);
x - независимая (объясняющая) переменная;
a,b - параметры регрессии;
ε - случайная составляющая.
Для расчета параметров a b линейной регрессии исп.формула:
na+b∑x=∑y
a∑x+b∑x2=∑xy
Интерпретация параметров эконометрической модели парной регрессии:
b - коэф. регрессии показателя силы связи, показывает насколько ед.изменится результат при изменении фактора на 1 ед. Знак “-” - связь обратная, “+” - связь прямая.
a - показывает, насколько в среднем за единицу времени изменится значение результативного признака y за счет воздействия всех факторов, кроме фактора x.
ε - случайная величина, включающая влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения.
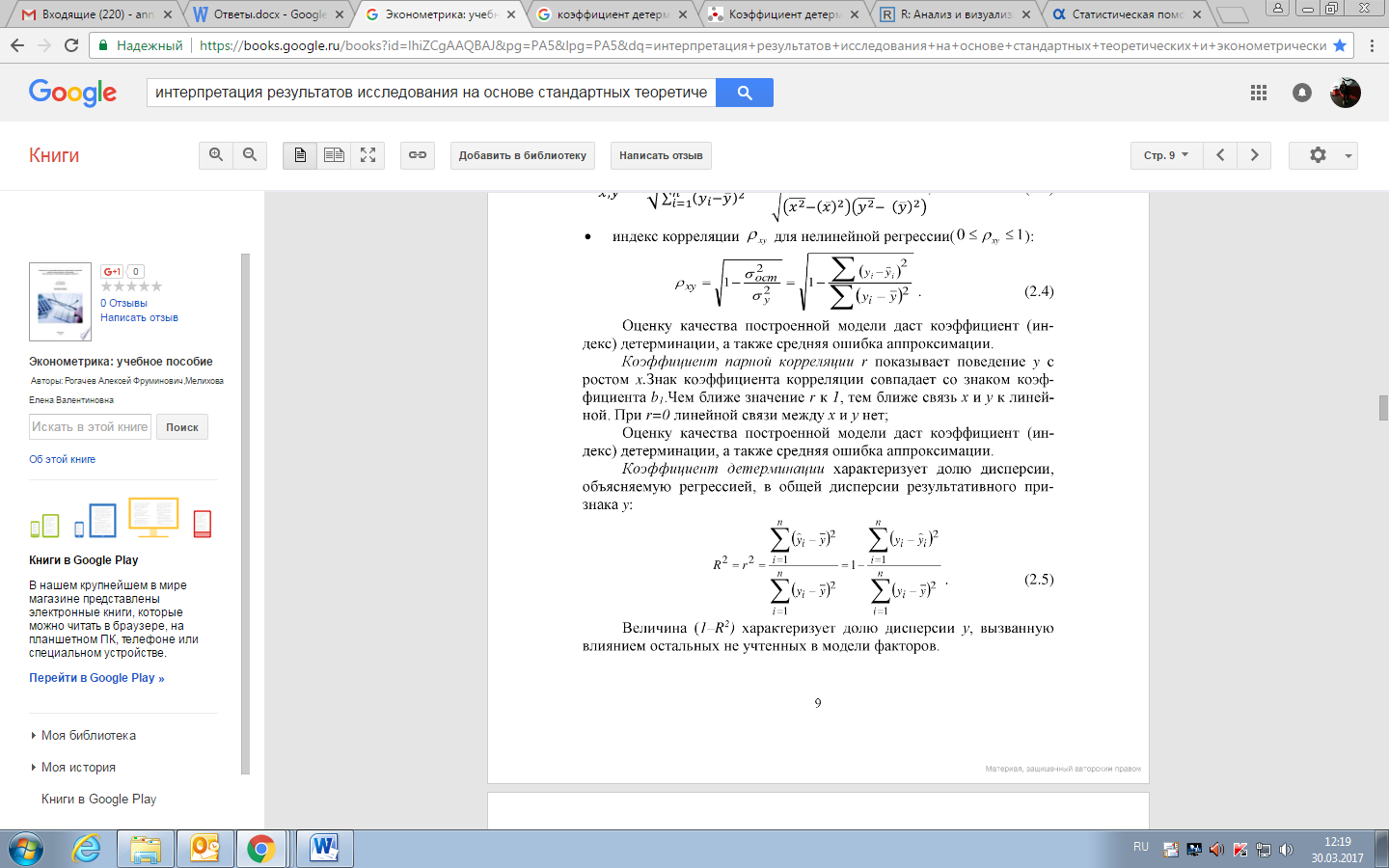
Оценку качества построенной модели даст коэффициент детерминации
Характеризует долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака
Интерпретация: вариация результата на R2% объясняется вариацией фактора Х, на долю неучтенных факторов приходится (1-R2)%.
Для оценка значимости уравнения регрессии применяется F-критерий Fнабл=(R2/1-R2)*((n-m-1)/m).