Дисконтирование с использованием сложной ставки

Математическое дисконтирование может применяться и с использованием сложной процентной ставки.

Приведенная стоимость по сложной процентной ставке определяется по формуле:

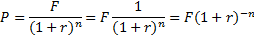(2.16)

Где 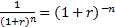- дисконтный множитель.

При начислении процентов m раз в году получим:

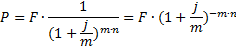(2.17)

В дисконтных операциях широко применяется сложная учетная ставка.

Дисконтирование осуществляется по формуле:

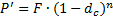(2.18)

Дисконт определяется по формуле:

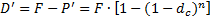
Величина сложной учетной ставки определяется по формуле:

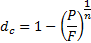(2.19)

При дисконтировании m раз в году используется номинальная учетная ставка.

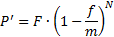(2.20)

Где f – номинальная учетная ставка;

N – общее число периодов дисконтирования ;

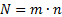(2.21)

Задания для самостоятельной работы

Задание 2.1.Банк ежегодно начисляет 8 % сложных. Клиент положил в банк 70 тыс. рублей. Какая сумма будет на его счете а) через 3 года; б) через 5 лет и 3 месяца.

Задание 2.2.На вашем счете 8 млн. руб. банковская ставка по депозитам равна 11% годовых, начисляется по схеме сложных ссудных процентов. Вам предлагают войти всем капиталом в организацию совместного предприятия, обещая удвоение капитала через 6 лет. Принимать ли это предложение?

Задание 2.3.За выполненную работу подрядчик должен получить 800 тыс. руб. Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок уплаты на 2 года, по истечении которых он обязуется выплатить 1030тыс. руб. Выгодно ли это предложение, если приемлемая норма прибыли составляет 10% какова минимальная ставка, которая делает подобные условия невыгодными для подрядчика?

Задание 2.4.Рассчитайте будущую стоимость 25 тыс.руб. для следующих ситуаций:1) 7 лет 9% годовых ежегодное начисление процентов;2) 7 лет 9 % годовых, полугодовое начисление процентов;3)7 лет 9% годовых, ежеквартальное начисление процентов.

Задание 2.5.Банк предоставил ссуду в размере 450 тыс.руб. на 39 месяцев под 15% годовых на условиях полугодового начисления процентов. Рассчитайте возвращенную сумму при различных способах начисления процентов:1) Схема сложных процентов; 2) Смешанная схема.

Задание 2.6.Вы положили в банк на депозит 390 тыс. руб. Банк начисляет сложные проценты по схеме: за первые 2 года – 4% годовых, а затем ставка увеличивается на 1 % каждый год. Определить какая сумма будет на вашем счете через 6 лет?

Задание 2.7.Депозит в размере 700 тыс. руб. внесен в банк на 4 года под 11% годовых, проценты сложные. Определить наращенную сумму, если: а) начисление процентов производится ежеквартально;б) начисление процентов производится ежемесячно.

Задание 2.8.На сумму 820 тыс. руб. ежеквартально по ставке 12% годовых начисляются сложные проценты в течение 17 месяцев определить величину наращенной суммы двумя методами.

Задание 2.9Предположим что выдан кредит в сумме 420 тыс.руб.на срок 3 года. Определить эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки 13%: а) при ежеквартальном начислении процентов; б) при полугодовом начислении процентов.

Задача 2.10.Кредит в размере 2 млн. руб. выдан на 4,5 года. По условиям договора начисление процентов производится по сложной учетной ставке 15% годовых. Определить наращенную сумму.

Задача 2.11.Предприниматель получил в банке ссуду в размере 970 тыс.руб. сроком на 6 лет на следующих условиях: для первого года процентная ставка равна 11% годовых, на следующие два года устанавливается маржа в размере 0,5% и на последующие годы маржа равна 0,8%. Найти сумму, которую предприниматель должен вернуть в банк по окончании срока ссуды.

Задание 2.12. Определить номинальную ставку, если эффективная ставка равна 19% и сложные проценты начисляются ежемесячно.

Задание 2.13. Из какого капитала можно получить 5 млн. руб. через 7 лет наращением сложными процентами по ставке 11% годовых, если наращение осуществлять: а)ежегодно; б) по полугодиям; в) ежеквартально; г) ежемесячно.

Задание 2.14. Долговое обязательство на выплату 370 тыс.руб. со сроком погашения через 7 лет учтено за 2 года до срока с дисконтом по сложной учетной ставке 9%. Найти величину дисконта.

Задание 2.15. Вклад в размере 200тыс.руб. помещен в банк на 7 лет. Предусмотрен следующий порядок начисления сложных процентов по плавающей годовой учетной ставке: в первые 2 года – 11% годовых, в следующие два года – 13%, в оставшиеся годы – 14% годовых. При использовании какой постоянной сложной учетной ставки можно получить такую же наращенную сумму.

Задание 2.16. Найдите величину дисконта, если долговое обязательство на выплату 400 тыс.руб. учтено за 4 года до срока погашения пот сложной учетной ставке а) 15% годовых; б)20% годовых.

Задание 2.17. По условиям финансового соглашения на сумму 110 тыс. руб. помешенную в банк на 5 лет, начисляются проценты по сложной учетной ставке 17% годовых. Определить наращенную сумму, если начисление процентов производится : а) по полугодиям; б) ежеквартально; в) ежемесячно. Сравнить полученные расчеты с результатами наращения сложными процентами по процентной ставке 17%.

Задание 2.18. Клиент имеет вексель на 600 тыс. руб., который он хочет учесть 01 июня текущего года в банке по сложной ставке, равной 8% годовых. Какую сумму он получит, если срок погашения векселя 01 октября текущего года?

Задание 2.19. Через 3 года вам понадобится для покупки автомобиля 950 тыс. руб. Вы располагаете в данный момент суммой 650тыс. руб. Под какую минимальную ссудную ставку нужно положить в банк деньги, чтобы накопить требуемую сумму?

Задание 2.20.Инвестиционный фонд предоставил кредит строительной фирме в размере 15 млн.руб. под 20% годовых (проценты сложные) на срок 5 лет. Определить дисконтированную величину и сумму дисконта, если инвестиционный фонд учел свой кредитный контракт в банке также под 20% годовых до срока погашения долга за: а) 4 года; б) 3 года; в) 2 года; г) полгода.

Задание 2.21. Определить современную величину 560тыс. руб., которые должны быть выплачены через 6 лет. В течение этого периода начислялись сложные проценты по ставке 9.5% годовых.

Задание 2.22.. Первоначальная сумма 2 млн. руб., помещенная в банк на 3 года в конце срока выросла до 2,3 млн. руб. Наращение производилось по сложной учетной ставке. Определить величину этой ставки.

Задание 2.24. Капитал в сумме 6 млн.руб. предоставлен в кредит на 6 лет под 20% годовых (проценты сложные). Определить значение наращенной суммы и приведенной величины на конец 3-го года (t=3).