Погашение потребительского кредита способом, когда процентный платеж рассчитывается методом счета «от ста»

Процентный платеж для первого месяца:

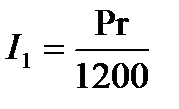(1.25)

Процентный платеж во втором месяце:

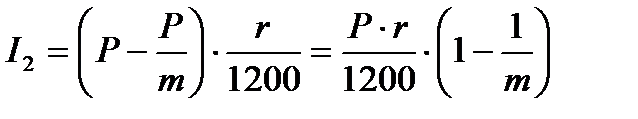(1.26)

Процентный платеж в третьем месяце:

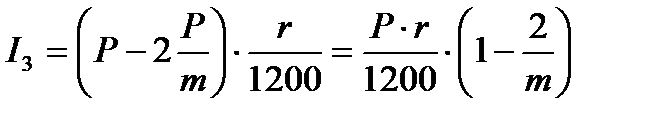(1.27)

Процентный платеж в месяце m:

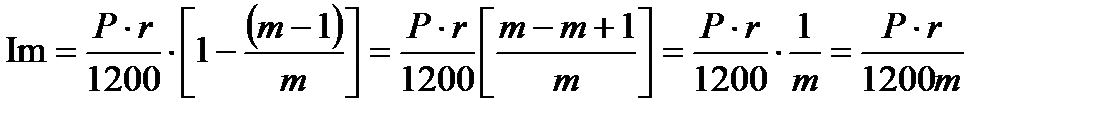(1.28)

Для определения общей величины процентных выплат за предоставленный кредит просуммируем их месячные значения:

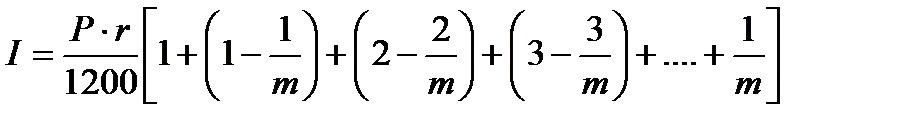(1.29)

откуда

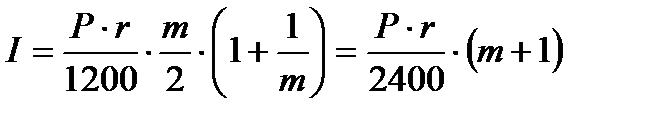(1.30)

Задания для самостоятельной работы

Задание 1.1.Банк выплачивает по пенсионным вкладам 10% годовых (проценты простые). Какая сумма будет у пенсионера на счету через год, если он положил на свой счет 120000 руб.

Задание 1.2.Вкладчик положил вклад, равный 40000 руб. в банк, выплачивающий 7% простых процентов в год. Какая сумма будет на счете вкладчика: а) через 3 месяца; б) через 1 год; в) через 3 года 5 месяцев; г) через 5 лет.

Задание 1. 3.Сумма 2 млн. руб.положена в банк 15 января не високосного года и востребована 25 декабря того же года. Ставка банка 8% годовых. Определить сумму начисленных процентов различными методами.

Задание 1.4.7 марта банк выдал кредит 700 тыс.руб. Срок возвратакредита 15 июля. Процентная ставка установлена 10% годовых. Год не високосный. Рассчитать наращенную сумму долга тремя методами.

Задание 1.5.В финансовом договоре клиента с банком предусмотрено погашение долга в размере 650 тыс. руб. через 90 дней при взятом кредите в размере 590 тыс. руб. Определить доходность такой сделки для банка в виде годовой процентной ставки при использовании банком простых обыкновенных процентов.

Задание 1.6.Какую сумму надо положить в банк выплачивающий 4% простых в год, чтобы получить 100тыс. руб.: а) через 4 месяца, б) через 1 год? В) через 4 года 6 месяцев?

Задание 1.7.Клиент обратился в банк за кредитом в сумме 1,5 млн. руб. на срок 180 дней. Банк согласился предоставить кредит на следующих условиях: проценты (12%) должны быть начислены и выплачены из суммы предоставления кредита в момент его выдачи. Определить сумму полученного кредита.

Задание 1. 8.За вексель, учтенный за 5 лет до срока погашения по учетной ставке 15% годовых, заплачено 5000 рублей. Определить номинальную стоимость векселя.

Задание 1.9.Финансовая компания дает ссуду в размере 80тыс.руб. на 4 года под простой дисконт, равный 8% в год. Какую сумму получит клиент в момент получения ссуды?

Задание 1.10.Предприятие берет в банке ссуду 5 млн. руб. на 3 месяца. Какую сумму должно вернуть предприятие, если возьмет ссуду под 11% простого дисконта?

Задание 1.11.Компания по производству мебели получила в коммерческом банке ссуду в 350 тыс. руб. на два года под простой дисконт, равный 12% в год. Какую сумму получила компания на руки?

Задание 1.12.Компания из задания 11 желает получить при тех же условиях на руки 350тыс.руб. Какую сумму она будет должна банку?

Задание 1.13.Какую сумму будет должна банку компания из задания 12, если она получит ссуду под 12% годовых (проценты простые). Что выгоднее компании взять ссуду под простой дисконт или под простые проценты?

Задание 1.14.Через один год владелец векселя выданного коммерческим банком, должен получить по нему 220 тыс. руб. Какая сумма была внесена в банк в момент приобретения векселя, если доходность векселя должна составить 10% годовых?

Задание 1.15.Владелец векселя номинальной стоимостью 220 тыс.руб. и сроком обращения 1 год, предъявил его банку-эмитенту для учета за 90 дней до даты погашения. Банк учет его по ставке 12%. Определить дисконтированную величину.

Задание 1.16.Вексель номинальной стоимостью 500тыс.руб. был учтен в банке за 90 дней до срока погашения по учетной ставке 16% . Определить дисконтированную величину векселя, используя антисипативный (предварительный) метод начисления процентов.

Задание 1.17.Долговое обязательство в сумме 200 тыс. руб. должно быть погашено через 90 дней с процентами 18% годовых. Владелец обязательства учел его в банке за 15 дней до наступления срока по учетной ставке 24% .Определить дисконт полученный банком.

Задание 1.18.Холодильник ценой 180 тыс.руб. продается в кредит на 2 года под 10 % годовых. Погасительные платежи вносятся через каждые 3 месяца. Определить размер разового погасительного платежа.

Задание 1.19.Кредит в сумме 100 тыс. руб. выдан на 3 года под 20% годовых (проценты простые). Погашение задолженности производится ежемесячными платежами. Составить план погашения задолженности.

Задание 1.20.Представлен потребительский кредит в размере 48 000руб. на срок 6 месяцев по 24 % годовых с ежемесячным погашением. Составить план погашения кредита (амортизации кредита).

Задание 1.21.Господин Смирнов Е.Г. поместил 240 тыс.руб. в банк на следующих условиях: в первые полгода процентная ставка равна 7% годовых. Каждый следующий квартал ставка повышается на 1 %. Какая сумма будет на счете через полтора года, если проценты начисляются на первоначальную сумму вклада? Какую постоянную ставку должен использовать банк, чтобы сумма по вкладу не изменилась?

Задание 1.22. Кредит выдается под простую ссудную ставку 15% годовых на 270 дней. Рассчитать сумму полученную заемщиком, и сумму процентных денег, если необходимо возвратить 620 тыс. руб.

Задание 1.23 Кредит в размере 950 тыс.руб. выдан по простой учетной ставке 17% годовых. Определить средний срок кредита, если заемщик планирует получить на руки 820 тыс.руб.

Задание 1.24. За выполненную работу по установке оборудования фирма должна получить 700 тыс.руб. Заказчик не имеет возможности рассчитаться в данный момент и предлагает отложить срок оплаты на 2 года, по истечении которых он обязуется выплатить 830 тыс.руб. Что выгоднее для фирмы – согласиться на условия заказчика или поучить сумму долга сейчас, и положить 700тыс. руб. в банк под 7,8% годовых

Задание 1.25. Вексель на сумму 70 тыс.руб. со сроком погашения через 4 года учтен за 32 месяца по простой учетной ставке 19% годовых. Определить суммы, которые получит предъявитель векселя при различных способах учета.

Задание 1.26. Долговое обязательство на выплату 580 тыс. руб. учтено за 4 года до срока погашения. Определить сумму полученную при учете этого обязательства, если производилось: 1) полугодовое; 2) поквартальное; 3) ежемесячное дисконтирование по простой учетной ставке 20% годовых

Задание 1.27. Вексель на сумму 600 тыс. руб. учитывается по простой учетной ставке за 120 дней до погашения с дисконтом 30тыс.руб. в пользу банка. Определить величину годовой учетной ставки при временной базе 360 дней в году.

Задание 1.28. В банк предъявлен вексель на сумму 600 тыс. руб. за полтора года до его погашения. Банк согласен учесть вексель по переменной простой учетной ставке, установленной следующим образом: первые полгода – 20% годовых, следующие полгода - 26% годовых, затем каждый квартал ставка повышается на 3 %. Определите дисконт банка и сумму, которую получит векселедержатель.

Тема 2. Сложные ставки

Сложные процентные ставки

В финансовой практике широко используются сложные проценты. Основное отличие сложных процентов от простых заключается в том, что база начисления процентов меняется от одного расчетного периода к другому. Сумма начисленных процентов добавляется к капиталу предыдущего периода, а начисление процентов в последующем периоде производится на эту, уже наращенную величину первоначального капитала.

Механизм наращения первоначальной суммы капитала по сложным процентам называют капитализацией.

Наращенная сумма по сложной процентной ставке в конце первого периода начисления будет равна:

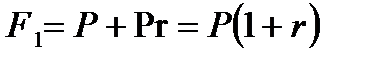(2.1)

Наращенная сумма в конце второго периода составит:

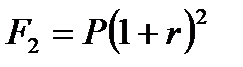(2.2)

В конце третьего года получим:

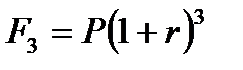(2.3)

К концу n-го периода сумма будет равна:

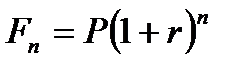(2.4)

В практике финансовых расчетов часто приходится вычислять суммы, наращенные за нецелое число периодов начисления.

Например, имеется необходимость знать наращенную сумму за полгода (n=0,5) или за 3 года 2 месяца (n=19/6) . В этом случае проценты начисляются двумя способами:

По схеме сложных процентов

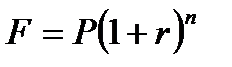(2.5)

где n=a+b –период сделки

a- целая часть года

b – дробная часть года

2. По смешанной схеме – сложные проценты за целое число лет и простые проценты для дробной части года.

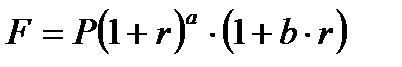(2.6)

Номинальная процентная ставка - годовая ставка процентов, исходя из которой, определяется величина ставки, применяемая в каждом периоде при начислении сложных процентов несколько раз в году.

Для начисления процентов m раз используется формула:

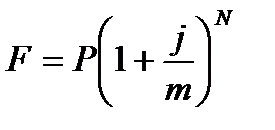(2.7)

где j – номинальная годовая процентная ставка

m – число периодов начисления процентов в году

N – число периодов начисления процентов за весь срок контракта;

n- число лет.

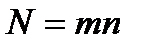(2.8)

Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена или по общей формуле, используемой при начислении сложных процентов, или по смешанному методу. В последнем случае наращенная сумма определяется по формуле:

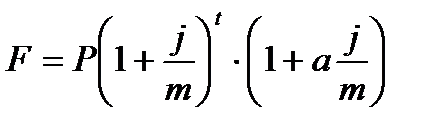(2.9)

где t– число полных периодов начисления процентов;

а – дробная часть одного периода начисления.

Эффективная процентная ставка — это сложная процентная ставка по кредиту, рассчитанная в предположении, что все платежи, необходимые для получения данного кредита, идут на его погашение.

Эффективная процентная ставка (ЭПС) - параметр, определяющий реальную стоимость кредита. Суть такова: когда человек хочет взять кредит в банке, он оценивает стоимость кредита по процентной ставке, которую указывает банк.

Эффективная ставка измеряет тот реальный относительный доход, который получает кредитор в целом за год. Иначе говоря, она отвечает на вопрос какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как при m –разовом начислении процентов в году по ставке j/m

Эффективная процентная ставка определяется по формуле:

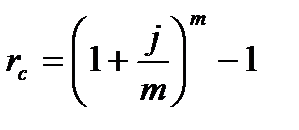(2.10)

Сложные учетные ставки

При использовании сложной годовой учетной ставки для определения параметров финансовой сделки используются следующие формулы:

Для определения суммы, получаемой заемщиком:

а) в конце первого интервала:

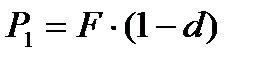(2.11)

б) в конце второго интервала:

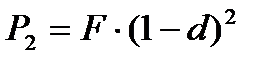(2.12)

в) через n лет:

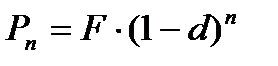(2.13)

Для определения наращенной суммы на основе сложных антисипативных процентов используют формулу:

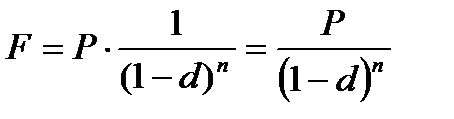(2.14)

где 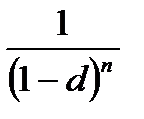- коэффициент наращения при вычислении сложных антисипативных процентов;

d – учетная ставка сложных процентов;

п- число лет.

При наращении сложных процентов по учетной ставке несколько раз в году (m раз) наращенная сумма определяется по формуле:

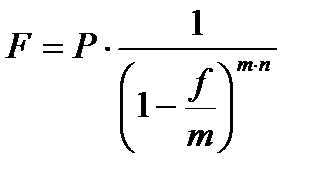(2.15)

где f – номинальная учетная ставка;

m- число периодов начисления процентов;

n- число лет.