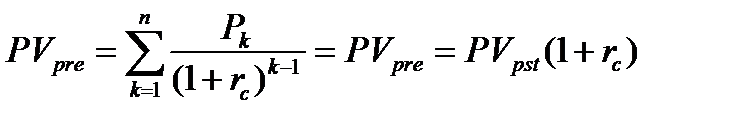Т.С. Сергеева – доц., канд.техн..наук
Учебно-методическое пособие
для практических занятий и самостоятельной работы студентов
факультета экономики и управления по направлению
подготовки 080100 « Экономика» (квалификация (степень) «Бакалавр»)
очного и заочного обучения
г. Нижний Новгород
Издательство ФБОУ ВПО ВГАВТ
2014 г.
УДК 336:657
К88
Рецензенты:
Т.С. Сергеева – доц., канд.техн..наук
Кудрявцева И.Ю., Почекаева О.В.
«Методы финансовых вычислений в учете и анализе»: учебно-методическое пособие для студ.очного и заочного факультета экономики и управления по направлению 080100 «Экономика» (квалификация (степень) «Бакалавр») /, И.Ю. Кудрявцева, О.В. Почекаева - Н.Новгород: Изд-во ФБОУ ВПО «ВГАВТ», 2014. – с.69
Учебно-методическое пособие по курсу «Методы финансовых вычислений в учете и анализе» предназначено для студентов очного и заочного обучения факультета экономики и управления ВГАВТа по направлению подготовки 080100 «Экономика» (квалификация (степень) «Бакалавр». В нем излагаются методические рекомендации по выполнению самостоятельных заданий.
Ответственный редактор – профессор, к.э.н., зав. кафедрой учета, анализа и аудита ВГАВТ Сивоволов Н.В.
Учебно - методическое пособие обсуждено и одобрено на заседании кафедры учета, анализа и аудита ВГАВТа __________
ã ФБОУ ВПО «ВГАВТ», 2014
Введение
Финансовые вычисления появились с возникновением товарно-денежных отношений и являются одной из основных базовых составляющих коммерческого дела.
В отдельную отрасль знания финансовые вычисления оформились только в XIX в: они назывались "коммерческие вычисления" или "коммерческая арифметика". Как утверждал русский математик, финансист и бухгалтер Н.С. Лунский, коммерческая математика изначально существовала под именем "политической арифметики", родоначальником которой является английский экономист Вильям Петти, – отец политической экономии и родоначальник статистической науки.
Быстрый экономический рост стран в XIX в. во многом был обусловлен распространением коммерческих знаний. В частности, в России действия правительства привели к тому, что к концу XIX в. появились коммерческие училища, торговые школы, классы, курсы, поскольку актуальность и важность коммерческого образования не у кого не вызывала сомнения, а основу коммерческих наук составляла коммерческая арифметика, так как именно она обуславливает каждый торговый акт, каждую финансовую операцию.
В послереволюционный период коммерческая арифметика в России не получила должного развития, поскольку многие вопросы, связанные с финансами и финансовыми расчетами, попросту игнорировались. В странах с ориентацией на рыночную экономику коммерческая арифметика развилась в самостоятельное направление в науке – в финансовую математику.
Российская экономика все более интегрируется в мировую экономику, что требует использования финансового инструментария, применяемого развитыми странами и международными организациями в финансовой практике.
Становление рыночных отношений в России сопровождается появлением навыков и методов, которыми приходится овладевать для оценки инвестиционных проектов, в операциях на рынке ценных бумаг, в ссудо-заемных операциях, в оценке бизнеса и др.
Кардинальное изменение банковской системы, внедрение новых форм собственности, развитие фондового рынка и финансовой самостоятельности предприятий сделали актуальным управление финансовыми ресурсами, одним из краеугольных элементов которого являются финансовые вычисления, базирующиеся на понятии временной ценности денег.
В этих условиях обоснованность принимаемых управленческих решений (а многие из них по сути своей имеют финансовую природу) в значительной степени определяется качеством финансово-аналитических расчетов.
При подготовке экономистов, финансистов, бухгалтеров, коммерсантов, менеджеров и маркетологов большое внимание уделяется изучению теории и практики финансово-экономических расчетов, необходимых в анализе инвестиционных проектов, расчете кредитных и коммерческих операций, эффективности предпринимательской деятельности, в страховом деле.
Тема 1. Простые ставки
Простые процентные ставки
Процесс движения денежных потоков от настоящего к будущему – называется наращением.
Процесс движения денежных средств от будущего к настоящему – дисконтированием.
При наращении определяется будущая стоимость денежных средств, при дисконтировании – текущая (сегодняшняя, дисконтированная) стоимость. При расчете будущей и текущей стоимости используется понятие процента.
Процент – плата, взимаемая за заем некоторой суммы денег.
На практике при проведении финансовых расчетов могут использоваться разные способы начисления процентов и разные виды ставок.
| Сложные ставки (dc) |
Учетная ставка — финансовый термин, финансовая категория, употребляемая для характеристики следующих процессов, связанных с кредитованием:
1. Под учётной ставкой понимается процентная ставка, по которой Банк России предоставляет кредиты коммерческим банкам. В российской практике наряду с термином учётная ставка для данной ситуации применяется термин ставка рефинансирования.
2. Под учётной ставкой понимается процент, курс, взимаемый банком с суммы векселя при «учёте векселя» (покупке его банком до наступления срока платежа). Фактически, учётная ставка в данном случае — это цена, взимаемая за приобретение обязательства до наступления срока уплаты. При учёте Банком России государственных ценных бумаг или предоставлении кредита под их залог применяется термин официальная учётная ставка.
В свою очередь и процентные и учетные ставки подразделяются на простые и сложные.
Существуют два способа начисления процентов:
1) декурсивный способ начисления (процентная ставка). Проценты начисляются в конце каждого интервала начисления.
2) антисипативный (предварительный) способ начисления -проценты начисляются в начальный момент времени, поэтому заемщик получает на руки сумму за вычетом процентных денег.
Процентная ставка характеризует доходность кредитной сделки. Она показывает, какая доля от суммы выданного кредита будет возвращена владельцу капитала в виде дохода. Величина процентной ставки определяется отношением:
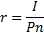 | (1.1) |
где r - процентная ставка;
I - величина дохода владельца капитала;
Р – сумма капитала предоставляемого в кредит;
n – срок ссуды в годах.
Величина процентного дохода определяется по формулам:
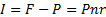 | (1.2) |
Где F – наращенная сумма.
Формула  определения наращенной суммы с использованием простых процентов (формула простых процентов) запишется в следующем виде:
определения наращенной суммы с использованием простых процентов (формула простых процентов) запишется в следующем виде:
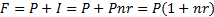 | (1.3) |
При использовании простых процентов, когда срок финансовой сделки не равен целому числу лет, периоды начисления процентов выражают дробным числом:
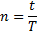 | (1.4) |
где t – число дней функционирования сделки( число дней на которое предоставлен кредит);
Т – временная база (число дней в году).
Формула наращенной суммы с использованием простых процентов примет вид:
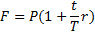 | (1.5) |
Различают три метода процентных расчетов, которые зависят от выбранного периода начисления:
1. Точные проценты с точным числом дней ссуды (английская практика). Продолжительность года принимается равной 365 (366) дней, а продолжительность месяцев – в днях, также соответствующих календарному исчислению, т.е. 28,29,30,31 день.
Точное число дней ссуды определяется по специальным таблицам как разность порядкового номера дня окончания ссуды и порядкового номера дня выдачи ссуды.
2. Обыкновенные проценты с точным числом дней ссуды (французская практика). Продолжительность года принимается , равной 360 дней, а продолжительность месяца соответствует календарному исчислению.
3.Обыкновенные проценты с приближенным числом дней ссуды (германская практика). Продолжительность года принимается равной 360 дней, продолжительность месяцев по 30 дней в каждом, начиная с момента выдачи ссуды и до момента ее погашения, и точным числом дней ссуды в неполном месяце.
При использовании Германской и Французской практики день выдачи и день погашения ссуды считается за один день.
Простые учетные ставки
Наряду с декурсивным методом существует и другой способ начисления процентов. Суть его сводится к тому, что проценты начисляются в начале расчетного периода, при этом базу (100%) принимается сумма погашения долга. В этом случае применяется не процентная ставка (r), а учетная ставка (d). Такой метод начисления процентов носит название антисипативный (предварительный). При антисипативном способе начисления процентов сумма получаемого дохода рассчитывается исходя из суммы, получаемой по прошествии интервала начисления (то есть наращенной суммы). Эта сумма и считается величиной получаемого кредита (ссуды). Т.к. проценты в данном случае начисляются в начале каждого интервала начисления, заемщик получает сумму кредита за вычетом процентных денег. Такая операция называется дисконтированием по учетной ставке или коммерческим (банковским) учетом.
Дисконт – это доход, полученный по учетной ставке, то есть разница между размером предоставляемого кредита и непосредственно выдаваемой ссудой.
Введем обозначения:d - годовая учетная ставка; Р - сумма, получаемая заемщиком; F – сумма подлежащая возврату.
Для расчета показателей используемых при предоставлении кредита используются формулы:
1. Для определения суммы, получаемой заемщиком :
а) в конце первого интервала:
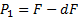 | (1.6) |
б) в конце второго интервала:
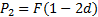 | (1.7) |
в) на весь период кредитования
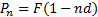 | (1.8) |
2. Для определения наращенной суммы:
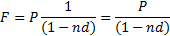 | (1.9) |
3. Для определения суммы, получаемой заемщиком при периоде начисления, не равным году:
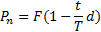 | (1.10) |
4. Для определения наращенной суммы при периоде начисления не равном году:
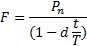 | (1.11) |
5. Для определения наращенной суммы при использовании разных ставок на разных интервалах начисления:
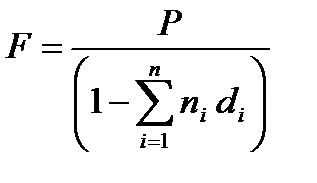 | (1.12) |
Тема 2. Сложные ставки
Сложные процентные ставки
В финансовой практике широко используются сложные проценты. Основное отличие сложных процентов от простых заключается в том, что база начисления процентов меняется от одного расчетного периода к другому. Сумма начисленных процентов добавляется к капиталу предыдущего периода, а начисление процентов в последующем периоде производится на эту, уже наращенную величину первоначального капитала.
Механизм наращения первоначальной суммы капитала по сложным процентам называют капитализацией.
Наращенная сумма по сложной процентной ставке в конце первого периода начисления будет равна:
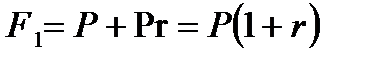 | (2.1) |
Наращенная сумма в конце второго периода составит:
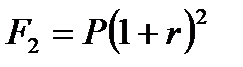 | (2.2) |
В конце третьего года получим:
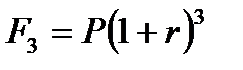 | (2.3) |
К концу n-го периода сумма будет равна:
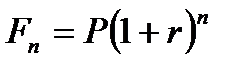 | (2.4) |
В практике финансовых расчетов часто приходится вычислять суммы, наращенные за нецелое число периодов начисления.
Например, имеется необходимость знать наращенную сумму за полгода (n=0,5) или за 3 года 2 месяца (n=19/6) . В этом случае проценты начисляются двумя способами:
По схеме сложных процентов
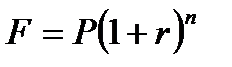 | (2.5) |
где n=a+b –период сделки
a- целая часть года
b – дробная часть года
2. По смешанной схеме – сложные проценты за целое число лет и простые проценты для дробной части года.
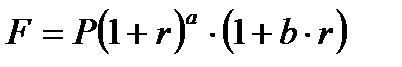 | (2.6) |
Номинальная процентная ставка - годовая ставка процентов, исходя из которой, определяется величина ставки, применяемая в каждом периоде при начислении сложных процентов несколько раз в году.
Для начисления процентов m раз используется формула:
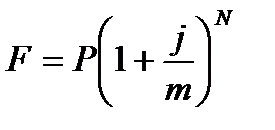 | (2.7) |
где j – номинальная годовая процентная ставка
m – число периодов начисления процентов в году
N – число периодов начисления процентов за весь срок контракта;
n- число лет.
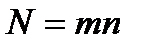 | (2.8) |
Если срок ссуды измеряется дробным числом лет, а начисление процентов производится m раз в году, то наращенная сумма может быть определена или по общей формуле, используемой при начислении сложных процентов, или по смешанному методу. В последнем случае наращенная сумма определяется по формуле:
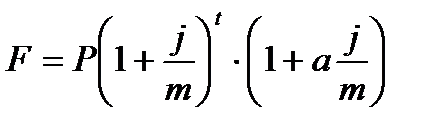 | (2.9) |
где t– число полных периодов начисления процентов;
а – дробная часть одного периода начисления.
Эффективная процентная ставка — это сложная процентная ставка по кредиту, рассчитанная в предположении, что все платежи, необходимые для получения данного кредита, идут на его погашение.
Эффективная процентная ставка (ЭПС) - параметр, определяющий реальную стоимость кредита. Суть такова: когда человек хочет взять кредит в банке, он оценивает стоимость кредита по процентной ставке, которую указывает банк.
Эффективная ставка измеряет тот реальный относительный доход, который получает кредитор в целом за год. Иначе говоря, она отвечает на вопрос какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как при m –разовом начислении процентов в году по ставке j/m
Эффективная процентная ставка определяется по формуле:
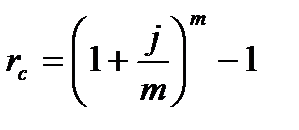 | (2.10) |
Сложные учетные ставки
При использовании сложной годовой учетной ставки для определения параметров финансовой сделки используются следующие формулы:
Для определения суммы, получаемой заемщиком:
а) в конце первого интервала:
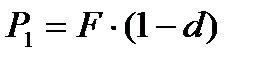 | (2.11) |
б) в конце второго интервала:
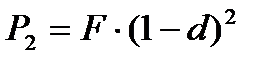 | (2.12) |
в) через n лет:
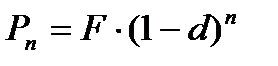 | (2.13) |
Для определения наращенной суммы на основе сложных антисипативных процентов используют формулу:
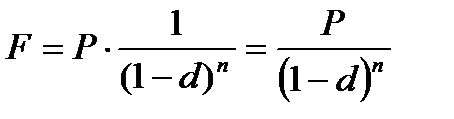 | (2.14) |
где 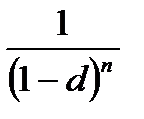 - коэффициент наращения при вычислении сложных антисипативных процентов;
- коэффициент наращения при вычислении сложных антисипативных процентов;
d – учетная ставка сложных процентов;
п- число лет.
При наращении сложных процентов по учетной ставке несколько раз в году (m раз) наращенная сумма определяется по формуле:
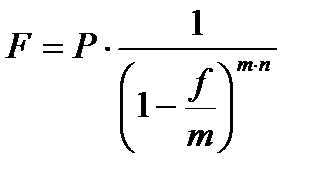 | (2.15) |
где f – номинальная учетная ставка;
m- число периодов начисления процентов;
n- число лет.
Равномерная амортизация.
Если срок службы равен n годам и первоначальная стоимость имущества S то его ежегодная стоимость уменьшается на (100/n)%, т.е. на S/n. Стоимость имущества в конце k-го года Sk вычисляется по формуле:
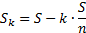 | (5.1) |
Правило суммы лет.
Реальный физический износ оборудования обычно идет быстрее в начале срока службы, чем в конце. Поэтому разработаны методы ускоренной амортизации. Если срок амортизации равен n лет, то вычисляем по формуле суммы арифметической прогрессии величину Kn – сумму номеров лет.
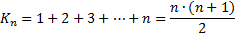 | (5.2) |
Величина амортизационных отчислений в i-м году равна:
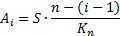 | (5.3) |
Метод двойного процента
Метод двойного процента заключается в том, что фиксированный процент снижения стоимости имущества r принимается равным удвоенному проценту снижения стоимости при равномерной амортизации. Такое снижение может продолжаться до конца срока амортизации, если стоимость имущества в последнем году будет остаточной. В этом случае снижение в последнем году увеличиваются так, чтобы стоимость в конце последнего года стала остаточной.
Тема 7. Конвертация валюты
Операции с девизами
Девизы – это все выраженные в иностранной валюте платежные средства. В процессе взаимного обмена национальных валют устанавливается их курс, называемый в зависимости от формы его выражения обменным или девизным. Обменный курс показывает, сколько единиц отечественной валюты можно получить в обмен на единицу иностранной. Девизный курс показывает, сколько единиц иностранной валюты можно получить за единицу отечественной.
Существует несколько вариантов обменных операций:
1. Обмен СКВ в количестве 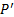 на рубли, наращение на полученную сумму P простых процентов по ставке r и конвертирование наращенной суммы F в исходную валюту, получая окончательно при этом сумму
на рубли, наращение на полученную сумму P простых процентов по ставке r и конвертирование наращенной суммы F в исходную валюту, получая окончательно при этом сумму 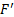 :
:
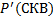 |
| F(Руб.) | 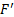 (СКВ) (СКВ) |
Конечная сумма операции в валюте определяется по формуле:
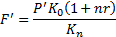 | (7.1) |
где n – срок депозита;
К0 – курс покупки СКВ в начале финансовой операции;
Kn - курс продажи СКВ в конце финансовой операции.
Доходность (результативность) такой операции в виде годовой процентной ставки определяется по формуле:
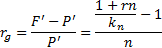 | (7.2) |
Где 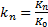
Если 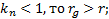
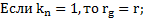
Если 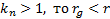
Критическое значение kn при котором rg=0 рассчитывается по формуле:
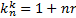 | (7.3) |
Критический курс продаж определяется по формуле:
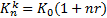 | (7.4) |
Величина Kn в начале финансовой операции неизвестна, поэтому полезно знать то ее значение, при котором двойное конвертирование не выгодно.
Если перед началом финансовой операции предполагают что курс Kn валюты в рублях будет меньше 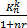 , то эту операцию проводить целесообразно.
, то эту операцию проводить целесообразно.
Если курс валюты больше 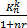 , то лучше воспользоваться просто депозитом в СКВ.
, то лучше воспользоваться просто депозитом в СКВ.
2. Финансовая операция имеет вид
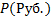 |
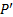 (CКВ) (CКВ) | 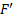 (СКВ) (СКВ) | F (Руб.) |
Конечная сумма операции в рублях определяется по формуле:
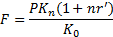 | (7.5) |
Для данной операции критическое значение и критический курс определяются по формулам (7.6) и (7.7) соответственно:
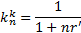 | (7.6) |
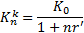 | (7.7) |
3. Формула 7.1 справедлива и для финансовой операции, при которой происходит двойная конвертация с участием двух видов валют, ни одна из которых не является рублями. Также эта формула справедлива и в частном случае, когда финансовая операция имеет вид:
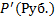 |
| F(Руб.) | 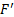 (Руб.) (Руб.) |
В этом случае К0=Kn=1, 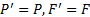
4. Наращение по простой учетной ставке с использованием схемы:
 |
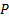 (Руб.) (Руб.) | 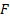 (Руб.) (Руб.) | 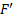 (СКВ) (СКВ) |
Конечная сумма операции в валюте определяется по формуле:
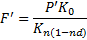 | (7.8) |
Доходность этой операции в виде простой годовой учетной ставки определяется по формуле:
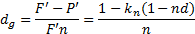 | (7.9) |
Находим критическое значение, при котором 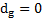
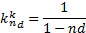 | (7.10) |
Критическое значение курса продажи находим по формуле:
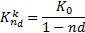 | (7.11) |
Двойная конвертация не доставляет никакой выгоды если:
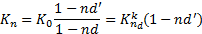 | (7.12) |
Тема 8. Денежные потоки
В процессе управления операционной и инвестиционной деятельностью организаций возникает необходимость в осуществлении специальных расчетов, связанных с движением денежных потоков в различные периоды. Ключевую роль в этих расчетах играет оценка стоимости (ценности) денег во времени. Концепция такой оценки исходит из предпочтительности денег сегодня, чем завтра. Многие предприниматели придерживаются этой методики, поскольку:
1) существует риск того, что деньги могут быть не получены в будущем;
2) если деньги имеются в наличии сегодня, то их можно вложить в бизнес с целью получения прироста авансированной стоимости (в форме прибыли) в текущем или будущем периодах.
Фактор времени, особенно в долгосрочных операциях, играет часто большую роль, чем размеры денежных сумм. Чтобы учесть его на практике, в коммерческих контрактах приводят соответствующие сроки и периодичность выплат. Необходимость учета временного фактора вытекает из экономической природы процессов финансирования, кредитования, инвестирования и выражается в принципе неравноценности денежных средств, относящихся к разным моментам времени.
Под влиянием инфляции, неопределенности и риска стоимость денег с течением времени изменяется также с учетом нормы прибыли, сложившейся на финансовом рынке. В качестве последней часто выступает ставка ссудного или депозитного процента, а также норма доходности по государственным ценным бумагам. В данном случае под процентом понимают сумму доходов, полученных инвестором (кредитором, вкладчиком) от использования денег на финансовом рынке.
Учитывая длительность инвестиционного процесса, приходится сравнивать стоимость денег при их возврате в форме будущих денежных поступлений (прибыли, основной суммы долга и др.), что требует проведения соответствующих финансовых вычислений.
Ранее были рассмотрены случаи финансовых операций, состоящих из отдельного разового платежа, например, получение и погашение долгосрочной ссуды. Вместе с тем, погашение такой ссуды возможно не только единовременным платежом, но множеством распределенных во времени выплат.
Потоки платежей являются неотъемлемой частью всевозможных финансовых операций: с ценными бумагами, в управлении финансами предприятий, при осуществлении инвестиционных проектов, в кредитных операциях, при оценке бизнеса, при оценке недвижимости, выборе альтернативных вариантов финансовых операций и т. п.
Потоки платежей весьма часто встречаются на практике. Заработная плата выплачивается, как правило, в виде потока платежей 2 раза в месяц, примерно через 15 дней. Плата за квартиру – поток, как правило, ежемесячных платежей. Семья откладывает на покупку автомобиля, внося ежемесячно на счет в банк некоторую сумму, и т.д.
Погашение долгосрочных банковских кредитов, облигационных займов, коммерческого кредита, инвестирование средств в различные программы (проекты), создание целевых денежных фондов в организациях, лизинговые и другие платежи часто предусматривают выплаты через определенные промежутки времени.
Ряд распределенных во времени выплат и поступлений называется потоком платежей.
Члены потока платежей – это величина каждого отдельного платежа.
Члены потока могут быть как положительными величинами (поступления), так и отрицательными величинами (выплатами), а временные интервалы между членами такого потока могут быть равными и неравными.
Если платеж осуществляется в конце временного интервала, то денежный поток называется постнумерандо, если вначале – пренумерандо.
При изучении потока платежей могут возникнуть две основные задачи.
Первая (прямая) задача предполагает суммарную оценку наращенного денежного потока (amount of cash flow), т.е. в ее основе лежит будущая стоимость (future value). В частности, если денежный поток представляет собой регулярные начисления процентов на вложенный капитал (P) по схеме сложных процентов, то в основе суммарной оценки наращенного денежного потока лежит формула (8.1).
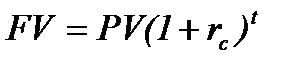 | (8.1) |
Логика решения прямой задачи постнумерандо представлена на рис. 8.1
| Р n |
| n-1 |
| n |
| Р 1 |
| Р 2 |
| Р 3 |
| Р 4 |
| Р 5 |
| Р n-1 |
Рис.8.1. Логика решения прямой задачи постнумерандо
На сумму Р1 будут начисляться проценты за период времени t=n-1 по формуле (8.2).
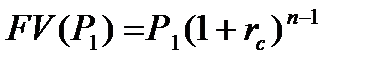 | (8.2) |
На сумму Р2 будут начисляться проценты за период времени t=n-2 по формуле (8.3).
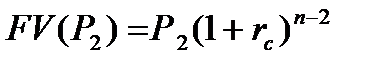 | (8.3) |
На сумму Рn-1 будут начисляться проценты за период времени t=1 по формуле (8.4).
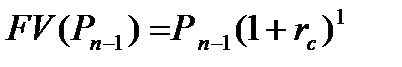 | (8.4) |
На сумму Pn проценты не начисляются. Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид (8.5) или (8.6).
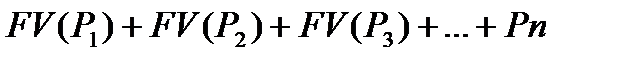 | (8.5) |
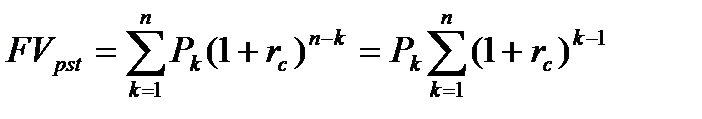 | (8.6) |
Слагаемые этой суммы являются членами геометрической прогрессии, первый член которой b1 = P, знаменатель q = 1+rc и число членов равно n. По формуле (8.7) находим сумму первых n членов этой геометрической прогрессии (8.8).
 | (8.7) |
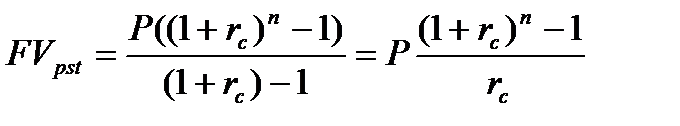 | (8.8) |
Вторая (обратная) задача предполагает суммарную оценку дисконтированного (приведенного) денежного потока (present value of cash flow). Поскольку отдельные элементы денежного потока генерируются в различные временные интервалы, а деньги имеют временную ценность, непосредственное их суммирование невозможно. Приведение денежного потока к одному моменту времени осуществляется с помощью формулы (8.9), выведенной из формулы (8.1).
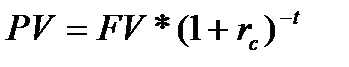 | (8.9) |
Логика решения обратной задачи постнумерандо представлена на рис. 8.2.
| Р 1 |
| Р 2 |
| Р 4 |
| Р 3 |
| Р 5 |
| Р n-1 |
| Р n |
| n-1 |
| n |





Рис.8.2. Логика решения обратной задачи постнумерандо
Основным результатом расчета является определение общей величины приведенного денежного потока (8.10).
| (8.10) |
Слагаемые этой суммы также являются членами геометрической прогрессии, первый член которой b1 = P(1+rc)-1, знаменатель q = 1/(1+rc) и число членов равно n. По формуле (8.5) находим сумму первых n членов этой геометрической прогрессии (8.11).
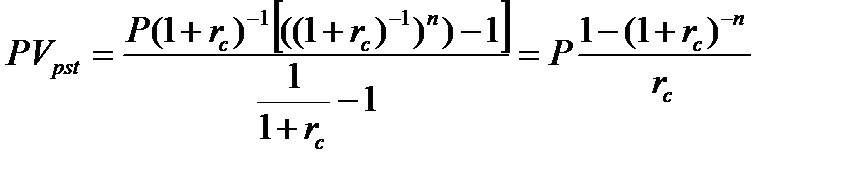 | (8.11) |
Логика решения прямой задачи пренумерандо (платеж в начале периода) представлена на рис. 8.3.
| Р 1 |
| Р 2 |
| Р 4 |
| Р 3 |
| Р 5 |
| Р n |
| n-1 |
| n |
Рис.8.3. Логика решения прямой задачи пренумерандо
На сумму Р1 будут начисляться проценты за период времени t=n по формуле (8.12).
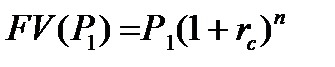 | (8.12) |
На сумму Р2 будут начисляться проценты за период времени t=n-1 по формуле (8.13).
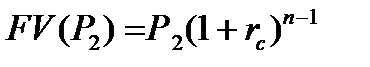 | (8.13) |
На сумму Рn будут начисляться проценты за период времени t=1 по формуле (8.14).
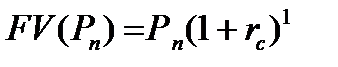 | (8.14) |
Следовательно, наращенный денежный поток для исходного потока постнумерандо имеет вид (8.15) или (8.16).
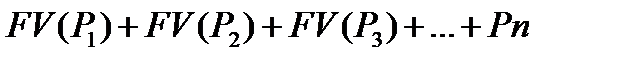 | (8.15) |
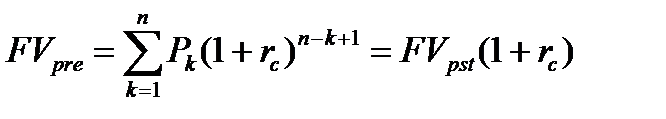 | (8.16) |
Логика решения обратной задачи пренумерандо представлена на рис. 8.4.
| Р 1 |
| Р 2 |
| Р n-1 |
| Р n |
| n-1 |
| n |





| Р 3 |
| n-2 |
Рис.8.4. Логика решения обратной задачи пренумерандо
Основным результатом расчета является определение общей величины приведенного денежного потока (8.17).
| (8.17) |
Таким образом, используемые расчетные формулы различны в зависимости от вида потока – постнумерандо или пренумерандо.
Тема 9. Финансовая рента
Поток платежей, все члены которого имеют одинаковое направление (знак), а временные интервалы между последовательными платежами постоянны, называется финансовой рентой или аннуитетом.
Финансовая рента (или просто рента) может быть охарактеризована рядом параметров:
1) член (элемент) ренты (P) – величина каждого отдельного платежа;
2) период ренты (t) – временной интервал между двумя платежами;
3) срок ренты (n) – время от начала реализации ренты до момента начисления последнего платежа;
4) процентная ставка (r) – ставка, применяемая для вычисления наращения или дисконтирования платежей, формирующих ренту.
Кроме перечисленных параметров, ренту характеризует ряд дополнительных показателей:
- количество платежей в течение года (p);
- частота начисления процентов, т.е. количество периодов в году, когда начисляют проценты (q);
- момент осуществления платежей (в начале, середине или в конце года) и др.
Поскольку условия финансовых сделок весьма разнообразны, постольку разнообразны и виды потоков платежей. В основе классификации финансовых рент положены различные качественные признаки:
1. В зависимости от периода продолжительности ренты выделяют:
- годовую ренту, которые представляют собой ежегодные платежи, т.е. период ренты равен 1 году;
- срочную ренту, при которой период ренты может быть как более, так и менее года.
2. По числу начислений процентов различают:
- ренты с начислением процентов один раз в год;
- ренты с начислением процентов несколько раз в год;
- непрерывное начисление.
3. По величине членов ренты могут быть:
- постоянные ренты, где величина каждого отдельного платежа постоянна, т.е. рента с равными членами;
- переменные ренты, где величина платежа варьируется, т.е. рента с неравными членами.
4. По числу членов ренты они бывают:
- с конечным числом членов (ограниченные ренты), когда число членов ренты конечно и заранее известно;
- с бесконечным числ