Номинальная и эффективная ставки процента

Допустим, что проценты капитализируются не 1 раз в год, а чаще, тогда можно использовать базовую ф., но обозначения меняем:

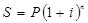
где n – общее число периодов роста

i – процентная ставка за соответствующий период

Но на практике чаще пользуются другим методом, т.к. обычно в договоре фиксируется годовая ставка.

Такая ставка обозначается j, число периодов начисления в году – m.

Тогда каждый раз проценты начисляются по ставке: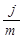

Ставка j наз. номинальной. Начисление процентов по номинальной ставке осуществляется по ф.:

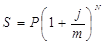
где N – количество периодов начисления всего

N= n ∙ m

где n – число лет

m – количество раз в год капитализации процентов

Эффективная ставка i измеряет тот реальный доход, который получают в целом за период. Можно сказать, что эффективная ставка показывает какая годовая ставка сложных процентов дает тот же финансовый результат, то и m-разовое наращение в год по ставке .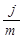

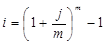
где m – количество раз в год капитализации процентов

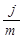- ставка капитализации

*Примечание: эффективная ставка больше номинальной (i > j).

Если нам необходимо определить j по известному i, то пользуемся ф.:

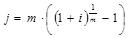
Определить номинальную и эффективную ставку процента можно и из базовых ф. наращения.

Эффективная из :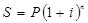

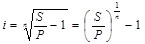
Номинальная из :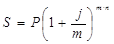

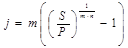
Дисконтирование по сложной процентной ставке

Из ф. наращенной суммы по сложным процентам выведем величину P:

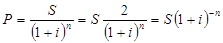
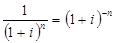- дисконтный множитель

При наращении процентов m-раз в год получаем следующую ф.:

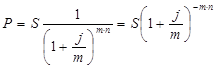
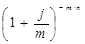- дисконтный множитель

Дисконт можно представить как S – P = D. Отсюда:

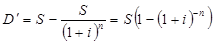
или

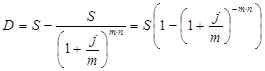
Дисконтирование по сложной учетной ставке

При операциях дисконтирования широко используется сложная учетная ставка. Ф. для дисконтирования имеет вид:

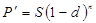
где d – сложная годовая учетная ставка

Ф. дисконта имеет вид:

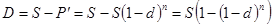
Преобразованием ф. 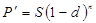можно выделить величину d:

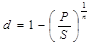
Эквивалентность процентных ставок

Иногда для принятия какого-либо финансового решения необходимо определить эквивалентность ставок процентов.

Эквивалентные процентные ставки – это такие ставки разного рода, применение которых при различных начальных условиях даст одинаковые финансовые результаты.

Для нахождения эквивалентных ставок процентов применяется уравнение эквивалентности, которое составляется по следующему принципу:

берется величина, которую можно рассчитать при использовании различных процентных ставок (обычно S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований выводим соотношение, выражающее зависимость между ставками процентов разного вида.