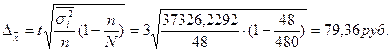Случайный бесповторный отбор.
Задача. Сколько следует проверить деталей для установления процента годности, чтобы с вероятностью 0,9973 ожидать отклонения выборочной доли от генеральной, не превышающей 5%. По прежним испытаниям 98% годовых деталей предлагается проводить через бесповторный отбор, объем генеральной совокупности N = 5000 шт. деталей.
Дано:
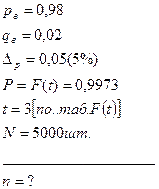 [30]
[30]
Решение:
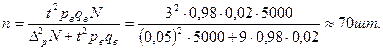
Вывод: Следует проверить не менее 70 образцов деталей, чтобы с вероятностью 0,9973 можно ожидать отклонения выборочной доли от генеральной, не превышающей 5%.
Механический отбор имеет формулу предельной ошибки выборки для случайного бесповторного отбора.
Типический бесповторный отбор
(для средней)
2-ый тип задач – определение вероятности того, что предельная ошибка выборки не превзойдет наперед заданного числа.
Задача. В магазине 3-х различных типов произведено обследование среднедневной выработки 10% продавцов. По каждому типу магазинов в случайном порядке была взято по 100 продавцов каждого типа. Причем:
– в магазине 1-го типа среднедневная выработка одного продавца оказалась равной 650 руб. при среднеквадратичном отклонении 50 руб.
– в магазине 2-го типа среднедневная выработка одного продавца – 600 руб. при среднеквадратичном отклонении – 30 руб.
– в магазине 3-го типа соответственно 575 руб. и 45 руб.
Какова вероятность утверждения, что среднедневная выработка всех продавцов, обследованных в магазинах, не будет больше или меньше среднедневной выработки продавцов, попавших в выборку на 1,75 руб.
Дано:
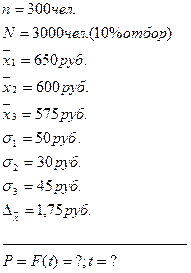
Решение:
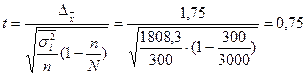 , где
, где
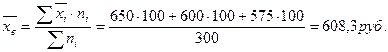
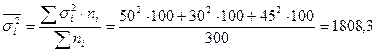
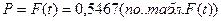 [31]
[31]
Вывод: С вероятностью 0,5467 можно утверждать, что среднедневная выработка всех продавцов, обследованных в магазинах не будет более 1,75 руб.
Типический бесповторный отбор (для средней)
1-ый тип задач – определение генеральной средней
(предельной ошибки выборки)
Задача. С вероятностью 0,9973 найти среднедневную выборку рабочих 2-х профессий слесарей и токарей в генеральной совокупности. Проведен 10% отбор. Имеются следующие данные:
Таблица 20[32]
Расчет основных выборочных характеристик.
Группа 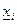 рабочих по дневной выборке (руб.) рабочих по дневной выборке (руб.) | Число 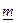 слесарей (чел.) слесарей (чел.) | 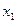 (середина интервала) (середина интервала) | 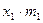 | 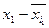 | 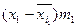 | 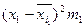 |
| A | 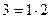 | 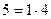 | 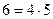 | |||
| до 500 | -391,67 | -783,4 | 306810,778 | |||
| 500-700 | -191,67 | -958,35 | 183686,944 | |||
| 700-900 | 8,33 | 83,3 | 693,889 | |||
| 900-1100 | 208,33 | 1249,98 | 260408,333 | |||
| св. 1100 | 408,33 | 408,33 | 166733,383 | |||
| Итого | 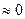 | 918333,333 | ||||
Группа 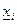 рабочих по дневной выборке (руб.) рабочих по дневной выборке (руб.) | Число 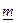 слесарей (чел.) слесарей (чел.) | 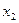 (середина интервала) (середина интервала) | 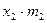 | 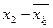 | 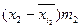 | 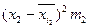 |
| A | 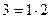 | 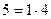 | 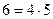 | |||
| до 500 | -416,67 | -416,67 | 173613,889 | |||
| 500-700 | -216,67 | -1083,35 | 234729,444 | |||
| 700-900 | -16,67 | -183,37 | 3056,7779 | |||
| 900-1100 | 183,33 | 916,65 | 168049,445 | |||
| св. 1100 | 383,33 | 766,64 | 293876,111 | |||
| Итого | 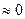 | 873325,667 |
Таблица 21
Расчет общей средней и средней из частных дисперсий.
| Группа рабочих | Среднедневная выработка (руб.) | Число 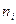 рабочих (чел.) рабочих (чел.) | 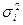 | 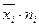 | 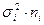 |
| Слесари | 791,67 | 38263,89 | 918333,333 | ||
| Токари | 816,67 | 36388,86 | 873325,667 | ||
| итого |
Выборочная среднедневная выработка рабочих равна:
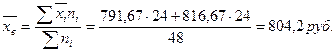 , где среднедневная выработка:
, где среднедневная выработка:
– слесарей 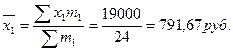
– токарей 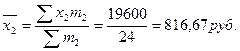
Выборочная средняя из внутригрупповых дисперсий равна:
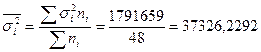 , где внутригрупповая дисперсия:
, где внутригрупповая дисперсия:
– слесарей 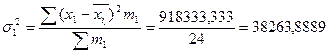
– токарей 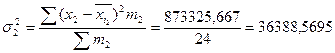
Итак, на основе следующих данных определим среднедневную выработку рабочих (слесарей и токарей) в генеральной совокупности.
Дано:
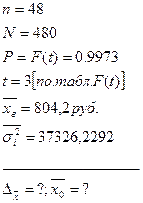 [33]
[33]
Среднедневная выработка рабочих в генеральной совокупности находится в следующих пределах:
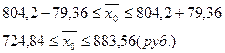 , где предельная ошибка выборки составляет:
, где предельная ошибка выборки составляет: