Способы обработки экономической информации.

К способам обработки экономической информации относятся расчеты абсолютных, относительных аналитических показателей, средних величин и показателей вариации; построение аналитических группировок, статистических таблиц, простых и комбинационных.

Для расчета абсолютных аналитических показателей используются данные статистического и бухгалтерского учета. Однако некоторые показатели определяются расчетным путем (например, сумма чистых активов, величина собственных оборотных средств и др.).

Относительные аналитические показатели представлены в виде долей единицы, коэффициентов, процентных чисел. К аналитическим показателям динамики относятся цепные и базисные абсолютные приросты, коэффициенты и темпы роста и прироста[1]

К относительным аналитическим показателям относятся статистические индексы, которые измеряют, сложное несоизмеримое явление во времени или в пространстве. Например, изучение динамики потребительской корзины населения. Статистические индексы определяются в виде агрегатных форм, средних форм индексов – количественного и качественного состава, а также индексов переменного и постоянного состава и индексов влияния структурных сдвигов[2].

Средние величины широко применяются в экономическом анализе. Средние величины являются обобщающими характеристиками качественно-однородной совокупности, именованной величиной, а также абстрактной величиной средней величины, как правило, не равны ни одному из вариантов. Существуют различные виды средних величин: средняя арифметическая простая и взвешенная, средняя гармоническая, средняя геометрическая, средняя хронологическая и др. Самой распространенной средней является средняя арифметическая. Простая средняя арифметическая величина применяется тогда, когда каждая единица статистической совокупности встречается один раз или одинаковое число раз. Она равна:

, где

х – единицы (вариант) статистической совокупности,

n – объем совокупности.

Средняя взвешенная арифметическая тогда, когда каждый вариант встречается неодинаковое число раз, в совокупности равна:

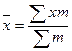, где

m – частота, которая показывает, сколько раз каждый вариант встречается в совокупности.

Например, при сдаче экзамена 24 студента получили следующие оценки: пять студентов пятерки, десять студентов четверки, шесть студентов тройки и три студента двойки. Надо найти средний балл студентов на экзамене.

Средний балл в группе равен:

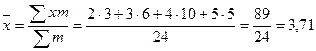балла

Средняя гармоническая величина применяется тогда, когда нет достаточно исходных данных для её расчета. Она равна:

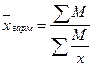, где

- произведение вариантов на соответствующие частоты.

Как показано выше средняя арифметическая взвешенная применяется тогда, когда известны варианты х и их частоты m. А средняя гармоническая взвешенная применяется тогда, когда отсутствует данные по частотам m, а представлено произведение вариантов на частоты .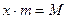

Рассмотрим среднюю цену яблок по трем магазинам по следующим данным.

Таблица 2