Теория экономического анализа

ТЕОРИЯ ЭКОНОМИЧЕСКОГО АНАЛИЗА

Учебное пособие

Москва

Введение

«Теория экономического анализа» является одной из основных дисциплин «экономического анализа». Для освоения курса необходимо изучить теоретические вопросы курса в сочетании с практическими навыками, что позволит студентам лучше понять и применить их при освоении других курсов экономического анализа.

Овладение «Теорией экономического анализа» её приёмами и методами требует от изучающих эту науку последовательной и систематической работы. Решение задач, выполнение упражнений способствует получению навыков при проведении экономического анализа.

Данное учебное пособие содержит программу изучения курса, краткие объяснения материала по каждой теме дисциплины, сопровождаемые решением типических задач, рекомендуемую литературу, вопросы для самопроверки, контрольные задания и тесты для аттестационного контроля по «Теории экономического анализа».

Для усвоения каждой темы даны методические указания по узловым вопросам, что может помочь студентам при самостоятельной проработке изученной темы.

Контрольные задания необходимо выполнять последовательно после проработки теоретических вопросов, методических указаний по темам и соответствующей литературы.

Для студентов заочного отделения необходимо выполнить все задания контрольной работы. Работы должны быть выполнены в отдельной тетради и обязательно содержать выводы.

Задачи контрольной работы могут быть использованы на практических занятиях по курсу «Теория экономического анализа» для студентов очной, очно-заочной, заочной и дистанционной формы обучения.

Программа курса и методические указания:

Курс «Теория экономического анализа» состоит из 8 тем:

Тема 1. Предмет, метод и задачи экономического анализа.

Тема 2. Информационная база экономического анализа и его основные виды.

Тема 3. Аналитические показатели и способы обработки экономической информации.

Тема 4. Методические основы экономического анализа.

Тема 5. Традиционные методы экономического анализа.

Тема 6. Детерминированный факторный анализ.

Тема 7. Метод корреляционного анализа.

Тема 8. Выборочный метод.

Тема 1. Предмет, метод и задачи экономического анализа.

План

1. Понятие экономического анализа.

2. Предмет экономического анализа и его содержание.

3. Роль экономического анализа в разработке и принятии управленческих решений.

4. Основные задачи экономического анализа.

Тема 2. Информационная база экономического анализа и его основные виды.

План

1. Виды источников информации экономического анализа. . . . . . . . . . . . 9

2. Виды пользователей экономической информации. . . . . . . . . . . . . . . . . 11

3. Классификация видов экономического анализа. . . . . . . . . . . . . . . . . . . 13

Тема 3. Аналитические показатели и способы обработки экономической информации.

План

1. Система аналитических показателей и их классификация. . . . . . . . . . 16

2. Способы обработки экономической информации. . . . . . . . . . . . . . . . . 18

Зависимость средней выработки рабочих от производственного стажа

(простая аналитическая таблица)

Группа рабочих по производственному стажу, лет	Число рабочих, чел	Выпуск продукции, шт.	Средняя выработка одного рабочих, шт./чел
А
до 1
1-5
5-10
свыше 10
Итого:

Таблица 6

Тема 4. Методические основы экономического анализа.

План

1. Метод экономического анализа и его особенности. . . . . . . . . . . . . . . . .26

2. Основные этапы экономического анализа и его методические приемы.

3. Способы проведения экономического анализа, их классифицируют:

Общая и частные методики экономического анализа.

Содержание методики экономического анализа.

Основные этапы выполнения аналитической работы.

Технические приемы и методы экономического анализа.

Способы проведения экономического анализа, их классифицируют

Содержание методики экономического анализа.

Методика экономического анализа включает:

ü цель и задачи экономического анализа;

ü характеристику объекта (элементы объекта);

ü выбор системы показателей исследуемого объекта;

ü рекомендации по периодичности и последовательности проведения экономического анализа;

ü характеристику способов анализа;

ü источники информации;

ü рекомендации по организации анализа с указанием конкретных служб или лиц;

ü указания по применению конкретных технических средств по обработке исходной информации;

ü указания о оформлению конкретно документов, которые бы отражали результаты анализа;

ü какие имеются потребители данного анализа.

Балансовый метод.

Балансовый метод основан на равенстве соотношений, пропорций, алгебраических сумм, отражающих взаимосвязь экономических показателей. Он предполагает сопоставление фактических данных с плановыми (или фактическими данными базового периода) и передвижение каких-то показателей за исследуемый период. Балансовый метод широко используется при анализе обеспеченности предприятия трудовыми, финансовыми ресурсами, сырьем, топливом, материалами, основными средствами производства, а также при анализе полноты их использования. Так, например, этот метод применяется для построения моделей, которые отражают взаимосвязь показателей производства и реализации продукции – товарный баланс:

Запасы на начало года + Поступление товара

=

Реализация товара + Прочие выбытия + Запасы на конец года

Для определения платежеспособности предприятия используется платежный баланс, в котором соотносятся платежные средства с платежными обязательствами. При изучении движения основных средств строятся балансы основных средств:

– по первоначальной стоимости:

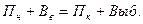
– по остаточной стоимости:

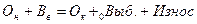за год, где

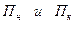– первоначальная стоимость на начало и на конец года,

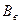– ввод основных средств за год,

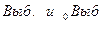– выбыло основных средств по первоначальной и остаточной стоимости,

Износ за год – физический износ основных средств за год.

Графический метод.

Графический метод занимает важное место в анализе, как способ отображения экономической информации и способ решения конкретных аналитических задач. Эти задачи решаются при изображении функциональной зависимости. Одновременно эти задачи решаются, например, при изображении функциональной зависимости с помощью линий на плоскости в системе координат, когда требуется рассчитать искомое значение результативного показателя при определенном значении факторного и одновременно показать характер зависимости показателей (зависимость затрат от объема производства). В экономическом анализе используется почти все виды графиков, диаграммы сравнения, диаграммы рядов динамики, кривые распределения, графики корреляционного поля, статистические картограммы (сочетание контурной карты местности (плана) с диаграммами). Особенно широко в анализе используются диаграммы сравнения – для сравнения отчетных показателей с плановыми или с данными предшествующих лет.

Эвристические методы.

В переводы с греческого «эврика» означает отыскиваю, нахожу, открываю. Еще Сократ поводил и извлекал в процессе беседы скрытое в человеке знания. В настоящее время под «эвристикой» понимается применение ряда логических приемов и методических правил и определение истины. Эвристика – наука, которая изучает продуктивное творческое мышление. Эвристические методы применяются при изучении рисков по экспертным оценкам.

Индексный метод

Рассмотрим на примере использование индексного метода.

Задача. Имеются данные о цене и количестве реализуемых товаров 2-х видов за 2-а смежных квартала. Определите индексы цен, физического объема и стоимости, а также показать индексную и факторная взаимосвязь.

Таблица 13

Метод цепных подстановок

Этот метод предусматривает проведение нескольких расчетов для изучения количественного влияния факторов на признак-результат. Однако в отличие от первых двух методов в этом методе при расчете учитывается последовательность. Сначала рассчитывается влияние количественного фактора, затем структурного и в последнюю очередь качественного. В случае, если модель состоит из нескольких факторов одного и того же вида, то выбирается, логически, сначала более весомый фактор. Следующей особенностью этого метода является то, что в расчетах производится последовательная замена базовой величины каждого из факторов, его фактической величиной, остальные факторы остаются неизменными. Причем, при изучении влияния последующих факторов, предшествующие берутся на уровне отчетного периода, а остальные – на уровне базисного. Так, при изучении влияния 2-го фактора, 1-ый берется на уровне отчетного периода, а остальные на уровне базисного периода. При расчете влияния 3-го фактора первые два берутся на уровне базисного периода. При расчете влияния 4-го фактора первые три берутся на уровне отчетного периода, а остальные – на уровне базисного периода и т.д. Если порядок подстановки не соблюдается, то влияние каждого фактора искажается, а сумма влияния всех факторов совпадает с общим отклонением признака-результата.

Надо отметить, что при цепном методе подстановки производится на один расчет меньше чем факторов. Если факторов четыре производится три расчета, если факторов три – два расчета, если факторов два – один расчет. Цепной метод может применятся во всех моделях детерминированного анализа (см. табл. 11).

Покажем, на примере задачи (см. табл. 12) – цепной метод подстановки детерминированного фактора анализа.

В алгоритме данной задачи: , первым фактором – количественным является – численность работников предприятия, вторым структурным – d-доля рабочих среди всех работников предприятия, третьим фактором – качественным – средняя выработка рабочих.

Многофакторная модель изменения выпуска продукции равна:

– изменение выпуска продукции в отчетном периоде по сравнению с базисным

за счет влияния:

– численности работников предприятия

– структуры рабочих среди всех работников предприятия

– средний выработки рабочих

Рассмотрим изменение факторов на выпуск продукции за счет:

- Изменение численности работников

- Изменение доли рабочих среди всех работников предприятия

- Изменение средней выработки рабочих

Многофакторная модель изменения выпуск продукции равна:

(см. гр. 7, табл. 12)

– изменение выпуска продукции

за счет влияния:

– численности работников предприятия

– структуры рабочих среди всех работников предприятия

– средний выработки рабочих

Термин «цепных подстановок» назван потому что вычитаемое первой разности – равно вычитателю второй разности, а вычитаемое второй разности равно вычитателю третьей разности – . И производится только два расчета: и .

Метод абсолютных разниц

Этот метод является упрощенным вариантом метода цепных подстановок. Абсолютное отклонение по первому фактору умножается на базовые значения остальных факторов. Затем абсолютное отклонение по второму фактору умножается на фактическое значение первого фактора и на базисные значения остальных факторов. В последующих расчетов абсолютное отклонение изучаемого фактора умножается на фактические значения предыдущих, рассмотренных факторов и на базисные значения последующих не рассмотренных факторов.

При использовании метода абсолютных и относительных разниц так же как и при методе цепных подстановок соблюдается последовательность расчета факторов. Этот метод может применятся в мультипликативных и смешанных моделях совмещающих мультипликативные и аддитивные модели (см.табл. 11).

На примере задачи (см. табл. 12) проиллюстрируем применение метода абсолютных разниц. Итак, многофакторная модель изменения выпуска составлена из следующих факторов:

Выпуск продукции в отчетном периоде по сравнению с базисным за счет:

- роста численности работников вырос на:

- увеличение доли рабочих среди работников вырос на:

- рост выработки рабочих вырос на:

Многофакторная модель изменения выпуска продукции равна:

(см. гр. 8, табл. 12).

Метод относительных разниц

Метод относительных разниц основан на методе цепных подстановок и индексном методе.

При этом методе, используются только мультипликативные модели (см. табл. 11) как произведение относительных отклонений индивидуальных индексов по изучаемому фактору за минусом единицы на индивидуальные индексы рассмотренных факторов и на абсолютное значение фактора-результата в базовом периоде. Так, при изучении влияния первого фактора (соблюдается очередность расчета факторов) абсолютное значение признака-результата базового периода умножается на индивидуальный индекс первого фактора за минусом единицы. При изучении влияния второго фактора абсолютное значение признака-результата базового варианта умножается на индивидуальный индекс первого фактора и на индивидуальный индекс второго фактора за минусом единицы. При изучении влияния третьего фактора фактор-результат базового периода умножается на индивидуальный индекс первых двух факторов и на индивидуальный индекс третьего фактора за минусом единицы и т.д.

Рассмотрим на примере (см. табл. 12) применение этого метода.

Многофакторная модель равна:

Прирост выпуска продукции обеспечивается:

- влиянием 1-го фактора численности работников на:

- влиянием 2-го фактора-доли рабочих среди всех работников

- влиянием 3-го фактора-выборки рабочих

Многофакторная модель изменения выпуска продукции равна:

(см. гр. 9, табл. 12).

Интегральный метод

При использовании интегрального метода очередность расчета факторов не имеет значения. Интегральный метод также как и другие математические методы (дифференциальный, логарифмический) убирают ту погрешность – совместного влияния факторов на признак-результат, которая присутствует при использовании предыдущих методов[7].

Интегральный метод применяется в мультипликативных, кратных и смешанных методах кратно-аддитивного вида (см. табл. 11).

В интегральном методе используется набор стандартных формул.

1. При двухфакторной мультипликативной модели:

- интегральный

– признак-результат

– признаки-факторы

Метод влияния факторов равен:

, где

и

2. При 3-х факторной мультипликативной модели: интегральный метод влияния факторов равен:

, где

Покажем этот метод на вышерассмотренном примере (см. табл. 12).

На выпуск продукции влияет изменение численности работников:

Влияние роста доли рабочих среди всех работников на рост выпуска продукции равно:

Рост выработки рабочих увеличивает выпуск продукции на:

Многофакторная модель изменения выпуска продукции равна:

(см. гр.10 табл. 12)

Показатели тесноты связи: коэффициент корреляции, эмпирическое корреляционное отношение (для сгруппированных данных), теоретическое корреляционное отношение (для сгруппированных и несгруппированных данных).

Показатели тесноты связи показывают, какой удельный вес занимает признак-фактор «x» среди всех факторов, влияющих на признак-результат – «y». Они отвечают на вопрос: насколько необходимо изучение данной связи между признаками и целесообразности её практического применения, а также позволяет выявить наиболее значимые факторы, которые являются решающими при формировании результативного признака.

Коэффициент корреляции[12] r является показателем тесноты связи. Он измеряется так же и направление зависимости.

Коэффициент корреляции равен:

Для сгруппированных данных:

Для не сгруппированных данных:

Если коэффициент корреляции принимает значение:

- от 0 до 0,45, то связь между х и y – слабая

- от 0,4 до 0,6, то связь между х и y – средняя

- от 0,6 до 0,8, то связь между х и y – сильная

- от 0,8 до 1 – очень тесная

Кроме того, коэффициент корреляции, как указано выше, показывает направление зависимости.

Если коэффициент корреляции принимает значение: от -1 до 0, то связь обратная.

Если коэффициент корреляции принимает значение от 0 до 1 – то связь прямая. Если = 0, то связь отсутствует, если = 1, то связь функциональная.

Коэффициент корреляции применяется только для прямолинейной связи.

Эмпирическое корреляционное отношение – ρ, которое является универсальным показателем тесноты связи, так как применяется для прямо или криволинейной зависимости. Но в отличие от коэффициента корреляции, этот показатель не показывает направления связи. Он применяется только для сгруппированных данных. Эмпирическое корреляционное отношение равно:

, где

- дисперсия по эмпирической линии регрессии

или - общая дисперсия

Степень тесноты связи у эмпирического корреляционного отношения такая же как у коэффициента корреляции.

При прямолинейной зависимости эмпирическое корреляционное отношение всегда будет немножко больше, чем абсолютное значение коэффициента корреляции.

Теоретическое корреляционное отношение – , где:

Для сгруппированных данных:

- дисперсия по теоретической линии регрессии

Расчет: общая дисперсия см. выше

Для несгруппированных данных:

- дисперсия по теоретической линии регрессии

- дисперсия по теоретической линии регрессии

- общая дисперсия

Поэтому, для несгруппированных данных теоретическое корреляционное отношение примет такой вид:

Теоретическое корреляционное отношение так же, как и эмпирическое корреляционное отношение является универсальным показателем, так как применяется при прямолинейной и криволинейной зависимости.

Степень тесноты связи у теоретического корреляционного отношения такая же как у коэффициента корреляции и у эмпирического корреляционного отношения.

При прямолинейной зависимости теоретическое корреляционное отношение будет всегда равно коэффициенту корреляции. А эмпирическое корреляционное отношение всегда будет незначительно больше теоретического корреляционного отношения.

Рассмотрим показатели тесноты связи для сгруппированных данных. Для расчета воспользуемся корреляционной таблицей зависимости товарной продукции «y» от производительности труда «х» (см. табл. 14).

Коэффициент корреляции равен:

или 63,5%, т.е. связь между производительностью труда и товарной продукцией будет тесная, прямолинейная корреляционная, на 63,5% изменения товарной продукции зависят от изменения производительности труда, и на 36,5% - от других факторов (учтенных и не учтенных).

Эмпирическое корреляционное отношение равно:

, где

Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 66% изменение товарной продукции зависит от изменения производительности труда.

Теоретическое корреляционное отношение равно:

или 63,5%

[13]

Таким образом, связь между производительностью труда и товарной продукцией будет тесная, корреляционная; на 63,5% изменение товарной продукции зависит от изменения производительности труда. Мы видим, что .

Далее рассчитаем показатели тесноты связи для несгруппированных данных на основе таблицы …

Коэффициент корреляции равен:

Связь между среднесуточным производством продукции и простоями будет обратная, довольно-таки тесная; т.е. на 94% среднесуточное производство зависит от снижения простоев, а на 6 % от других факторов.

Теоретическое корреляционное отношение равно:

Таким образом, связь между среднесуточным производством продукции и простоями будет довольно таки тесная и на 94% среднесуточное производство зависит от простоев.

При большом объеме выборки

При большой выборке, отобранной из генеральной совокупности нормального распределения, предполагается считать распредение коэффициента корреляции близко к нормальному со средней, равной «r» и дисперсией 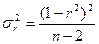, а среднеквадратическая ошибка коэффициента корреляции тогда будет равна:

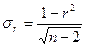, где

r – коэффициент корреляции выборочной совокупности;

n – объем выборки;

k = n – 2 – число степеней свободы при линейной зависимости.

Если величина 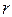> 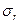в 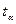раз, или 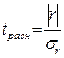> 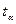[14]

Найдем для сгруппированных данных (см. таб. 14) среднюю квадратическую ошибку коэффициента корреляции:

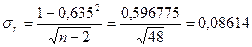, тогда

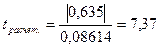
С вероятностью0,95 и числом степеней свободы k = 50 – 2 = 48, 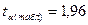[15].

Поскольку 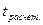> 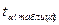, следует, что с вероятностью Р = 0,95 и числом степеней свободы k = 48 можно утверждать о существенности выборочного коэффициента корреляции, т.е. связь между х и y – значимая.

Для генеральной совокупности коэффициент корреляции будет находится в пределах.

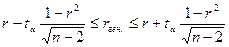
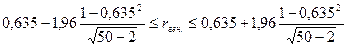
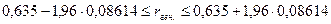
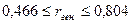
или

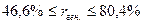
С вероятностью 0,95 можно утверждать, что коэффициент корреляции будет не ниже 46,6% и не выше 80,4%.

При малой выборки

Для малого объема выборочной совокупности 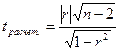для оценки значимости коэффициента корреляции.

Если 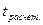> 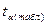, то расчетный коэффициент корреляции существенен и связь между х и y вполне реальна. Если 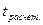< 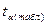, то связь между х и y несущественна и корреляционная связь в генеральной совокупности отсутствует.

По данным таблицы 15

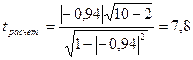, а с вероятностью 0,95 и числом степеней свободы k = 10 – 2 = 8, 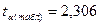[16].

Значит связь между х (простоями) и y – (выпуском продукции) существенна, т.к.

>

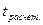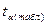
8. Проверка возможности использования прямолинейной функции – гипотезы Кендэла[17]о линейной корреляционной зависимости.

Для проведения гипотезы Кендэла о линейной зависимости определяется величина вероятности, которая рассчитывается по следующей формуле:

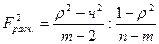[18], где

n – объем совокупности

m – число групп по признаку фактору х

Если критерий 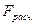найденный с определенной вероятностью и критериями свободы ( 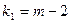и 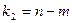) будут меньше F расчетного, то гипотеза о линейной связи между х и у отвергается. Если наоборот – то возможность использовать линейную функцию не опровергается.

По данным таблицы 14 рассчитаем этот критерий.

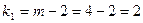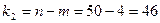Критерий свободы , а . С вероятностью 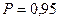, 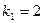и 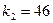табличное значение 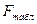- критерия [19] = 3,2.

Расчетный критерий равен:

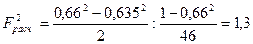
Поскольку 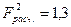меньше 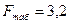, то это не позволяет отклонить гипотезу о линейной связи между производительностью труда – х и товарной продукцией – y.

Литература

1. Гусаров В.М., Проява С.М. Статистика: Уч. пособие для студентов вузов, занимающихся по экономическим специальностям – 2-е изд., перераб. и доп., ЮНИТИ-ДАНА, 2008, 207 с.

2. Елисеева И.И., Егорова И.И., Курышева С.В. и др. Статистика: Учебник / Под ред. Елисеевой И.И. – М.: Проспект, 2009. – 448 с. М.: Высшее образование, 2009 – 590 с.

3. Ефимова М.Р. Практикум по общей теории статистики, 2008, 368 с.

4. Ефимова М.Р., Петрова Е.В., Румянцов В.Н. Общая теория статистики: Учебник. 2-е изд., испр. и доп. – М.: ИНФРА – М, 2007. – 417 с. (Высшее образование).

5. Ильина Г.Г. Статистические приемы и методы в маркетинге: Учеб. пос. – М.: РосНОУ, 2004, 128 с.

6. Савицкая Г.В. Анализ хозяйственной деятельности предприятия. – Мн.: ИП «Экоперспектива», 2009, 530 с.

Вопросы для самопроверки

1. Что такое функциональные и корреляционные связи?

2. Какие задачи стоят перед корреляционным анализом?

3. Назовите виды корреляционной зависимости и рассмотрите их.

4. Как графически изображается корреляционная зависимость для несгруппированных и сгруппированных данных?

5. Эмпирическая линия регрессии и её характеристика.

6. Теоретическая линия регрессии и её характеристика.

7. Показатели тесноты связи и их характеристика.

8. Сущность коэффициента корреляции.

9. Характеристика эмпирического корреляционного отношения.

10. Теоретическое корреляционное отношение и его характеристика.

11. Простейшие показатели тесноты связи: коэффициент Фехнера, коэффициент корреляции рангов, коэффициент ассоциации.

12. Методы оценки существенности расчета коэффициента корреляции.

13. Гипотеза Кендела о линейной корреляционной зависимости.

Тема 8. Выборочный метод.

План

1. Общие понятия о выборочном методе и причины, вызывающие выборочное обследование.

2. Условия правильности проведения выборочного отбора.

3. Задачи выборки.

4. Способы отбора.

Способы отбора

Способы отбора определяют конкретный механизм отбора единиц из генеральной совокупности.

По степени охвата единиц совокупности разделяют большие и малые выборки (с объемом ).

Наибольшее распространение получили следующие виды выборки:

– собственно-случайная

– механическая

– типическая

– серийная (гнездовая)

Механическая выборка

При механическом отборе единицы для обследования отбираются уже не наудачу. При этой форме выборочного наблюдения единицы генеральной совокупности располагаются в каком-то порядке, но только не по изучаемому признаку, а, скажем, в алфавитном. Затем упорядоченная известным образом исходная совокупность делится на определенное число равных частей, и из каждой такой части отбирается одна единица – представитель с определенным порядковым номером (10-я, 20-я, 30-я). Например, при 10% выборке из совокупности в 1000 единиц она должна быть разделена на 100 равных частей, из которых могут быть отобраны 5-я, 15-я, 25-я и т.д. единицы.

5-я	15-я	25-я	…	985-я	995-я
			…980

Могут быть взяты и другие порядковые номера.

Таким образом, если при случайном отборе есть лишь возможность попадания в выборку единиц от всех частей генеральной совокупности, то механический отбор направлен на то, чтобы обеспечить попадание в выборку таких представителей. В этом смысле, механический отбор можно назвать направленным отбором, и поэтому, при правильной организации, он репрезентативнее случайного отбора.

Математическая статистика не располагает специальными зависимости для расчета средней ошибки выборки при механическом отборе, и она вычисляется по той же формуле, что и в условиях случайного бесповторного отбора. Следовательно, величина вычисленной таким образом средней ошибка механического отбора оказывается несколько завышенной.

Типическая выборка

Типический отбор также принадлежат к числу направленных видов отбора. При типическом отборе совокупность также разделяется на части, но не механически, а по каком-то типическому признаку. Например, для обследования бюджетов рабочих все рабочие данного предприятия предварительно группируются по профессиям, т.е. по признаку, который определяет уровень заработной платы. Затем из каждой группы производят случайный или механический отбор. При типическом отборе обеспечивается попадание в выборку представителей всех типических групп, что повышает репрезентативность выборочных данных.

Типичные группы могут быть как равными, так и не равными по численности. В последнем случае отбор производится пропорционально объему каждого типа во всей генеральной совокупности. Типический отбор бывает повторным и бесповторным.

Случайный отбор

1-ый тип задач – Определение предельной ошибки выборки.

Случайный повторный отбор

Задача. С какой вероятностью можно утверждать, что выборочная доля бракованных деталей будет отличатся от генеральной доли не более чем на 1%, если при измерении 115 деталей установлена доля брака равная 0,5%?

Дано:

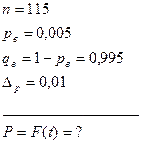
Решение:

Знаем, что:

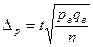
тогда 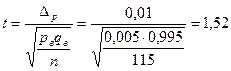, а вероятность 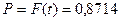(по таблице F(t))[29]

Вывод: С вероятностью 0,8714 можно утверждать, что выборочная доля бракованных деталей будет отличаться от генеральной доли не более чем на 1%.

3-ий тип задач – Определение минимального объема выборки

Задача 2. «К»

По предприятию имеются следующие данные о выпуске продукции.

В соответствии с вашим вариантом

Требуется:

1.Заполнить недостающие показатели в таблице

2.Определить средний процент выполнения плана по 5-ти изделиям. Сделайте вывод.

3.Определить структуру планового и фактического выпуска продукции, изобразите графически.

Задача 3.

Определите относительные величины планового задания по снижению себестоимости и динамики себестоимости производства автомобиля, если в 2011 г.себестоимость грузового автомобиля КамАЗ-55111 составил 170 тыс.руб., по плану на 2012 г.предусмотрено снизи