Задача №2. Абсолютная (G90) и относительная (G91) системы счисления
ФГБОУ ВПО Пермский национальный исследовательский политехнический университет
Кафедра «Инновационные технологии машиностроения»
Методические указания по дисциплине
«ОСНОВЫ ЧИСЛОВОГО ПРОГРАММНОГО УПРАВЛЕНИЯ»
Примеры решения задач
г. Пермь, 2016
ОСНОВЫ ЧИСЛОВОГО ПРОГРАММНОГО УПРАВЛЕНИЯ
Краткие теоретические сведения
G команды
G90 – абсолютная система счисления. Наиболее распространенная.
G91 – относительная система счисления. Применяется при разработке подпрограмм и пользовательских циклов.
G00 – движение к конечной точке с максимально возможной скоростью.
Формат кадра:
G00 X.. Y.. Z..
G01 – прямолинейное движение к конечной точке с заданной подачей.
Формат кадра:
G01 X.. Y.. Z.. F..
G02 – круговая интерполяция по часовой стрелке.
G03 - круговая интерполяция против часовой стрелке.
Формат кадра:
G17 (G18,G19)
G2/G3 X.. Y.. (Z..) I.. J.. (K..) F.. – конечная точка и центр окружности
G04 – выдержка времени.
Формат кадра:
G4F – в секундах
G4S – в оборотах шпинделя
G17/G18/G19 – плоскости интерполяции XY/XZ/ZY соответственно.
Требуются для функционирования команд G2/G3 и G41/G42.
G54, G55, G56, G57 – выбор смещения ноля (W) из таблицы смещения нолей.
G53 – отказ от всех смещений ноля и работа в машинной системе координат.
T – выбор инструмента из магазина.
D – выбор номера корректора на инструмент из таблицы корректоров. Максимальное количество 9 значений. По умолчанию D1
G41/G42 – ввод корректора слева/справа от материала.
G40 – вывод корректора.
Формат кадра:
G17 (G18, G19) – включение плоскости интерполяции
G41/G42 G01 X… Y… (Z) F… – ввод корректора
X… Y… (Z…) – работа по контуру
G40 X… Y… (Z…) - вывод корректора
Обороты
S – задание оборотов шпинделя.
G96 – обороты шпинделя в м/мин
G97 – обороты шпинделя в об/мин
LIMS – максимально допустимые обороты шпинделя в об/мин
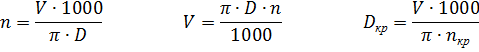
Подача
F – задание подачи.
G94 – подача в мм/мин
G95 – подача в мм/об
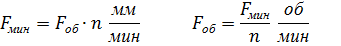
Для фрезерования 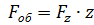
М команды
M00 – безусловный останов
M01 – условный останов
M02 – конец программы с возвратом в начало
M03 – вращение шпинделя по часовой стрелке
M04 - вращение шпинделя против часовой стрелке
M05 – стоп шпинделя
M06 – смена режущего инструмента
M07 – подача СОЖ №1
M08 – подача СОЖ №2
M09 – остановка подачи СОЖ
Вспомогательные и служебные адреса
N – имя кадра, номер кадра
: - имя главного кадра
/ - пропускаемый кадр
; - комментарий, исключает кадр из последовательности программы
Задача №1. Определение координат опорных точек контура
Необходимо определить координаты опорных точек данного контура (рис.1)
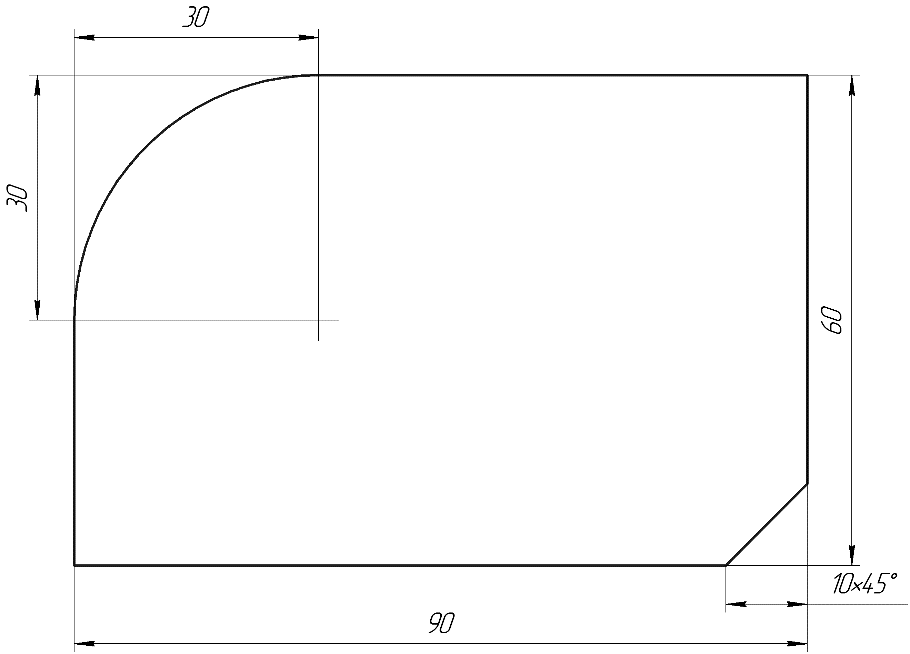
рис. 1.
Алгоритм решения.
1. Обозначим опорные точки контура (рис.2). Точки необходимо расставлять на месте стыка элементарных геометрических фигур (линий, дуг)
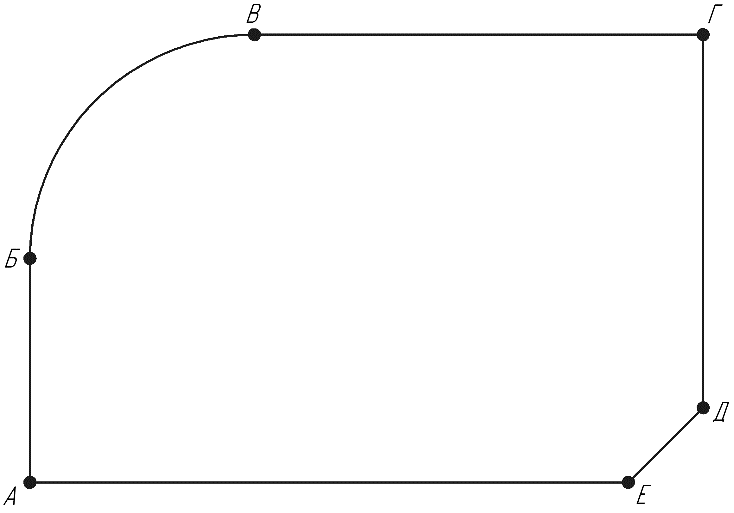
рис.2.
2. Выберем наиболее удобную для измерений точку, которую примем в качестве центра (ноля) системы координат. В данном случае т.А - центр системы координат (рис.3).
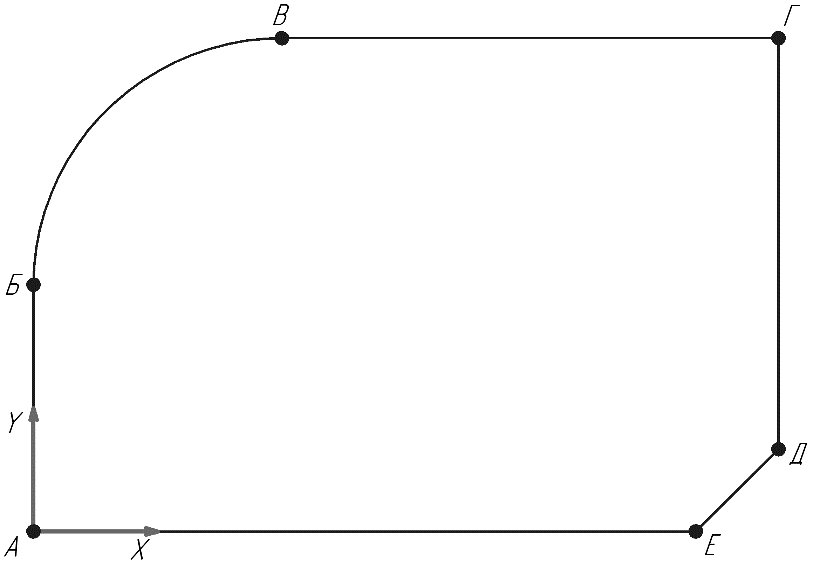
рис.3.
3. Произведем скалывание координат опорных точек (рис.4)
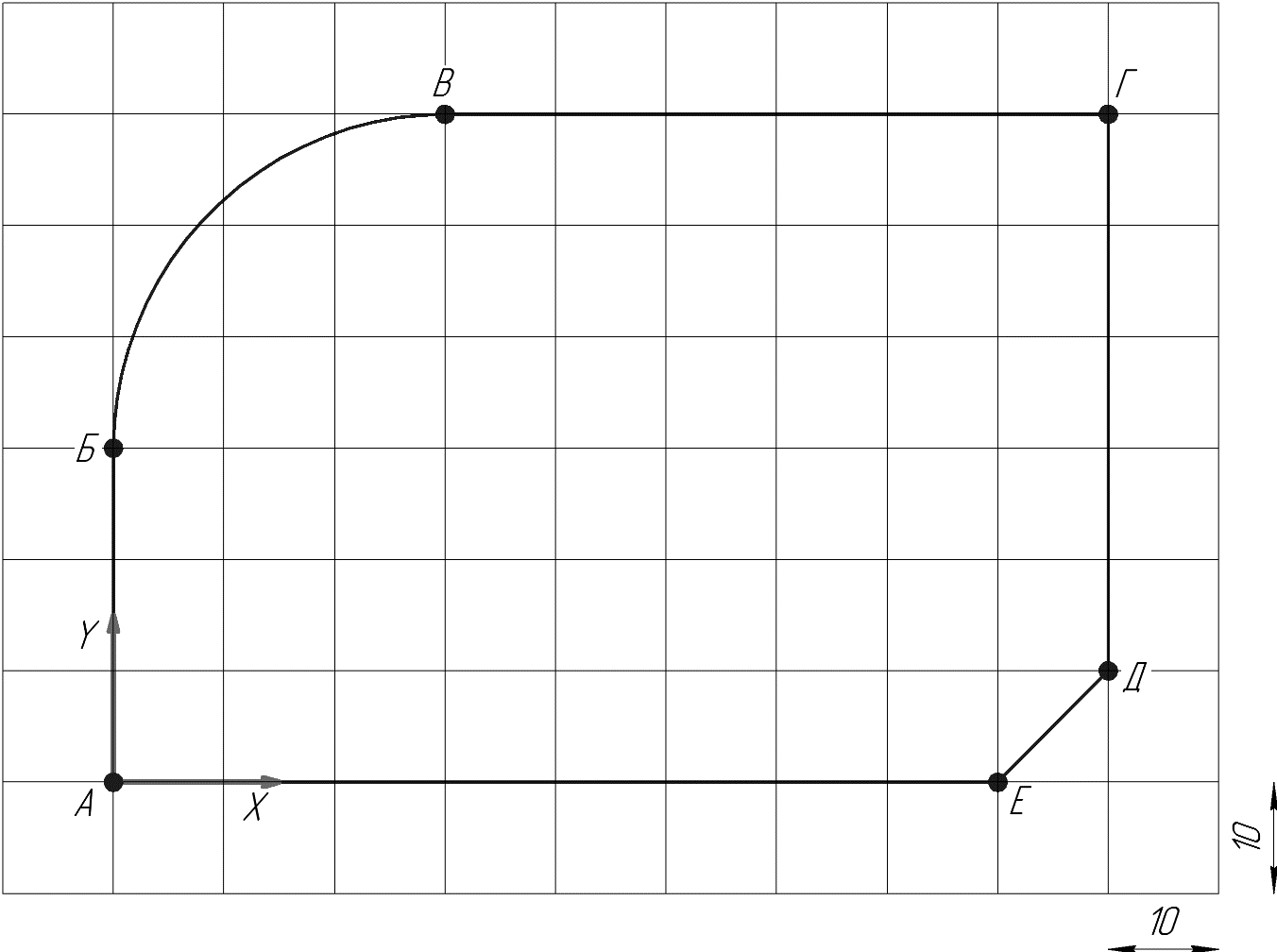
рис.4.
В результате получим следующие значения координат:
т. А X0 Y0
т. Б X0 Y30
т. В X30 Y60
т. Г X90 Y60
т. Д X90 Y10
т. Е X80 Y0
Задача №2. Абсолютная (G90) и относительная (G91) системы счисления
Необходимо рассчитать координаты опорных точек контура (рис.5) в абсолютной (от базового ноля) и относительной (от положения в данный момент времени) системах координат.
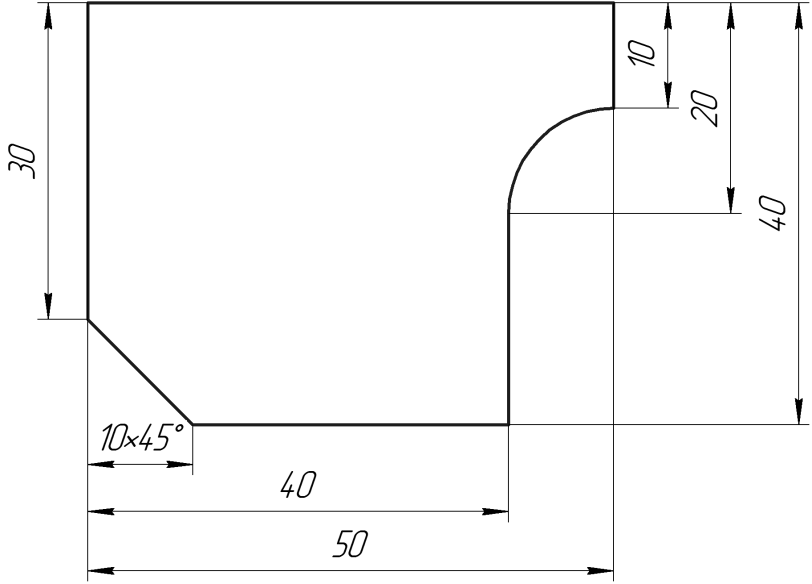
рис.5.
Алгоритм решения
Абсолютная система счисления
Выполняем алгоритм решения аналогично задаче №1, но для контура рис.5. Получим рис.6
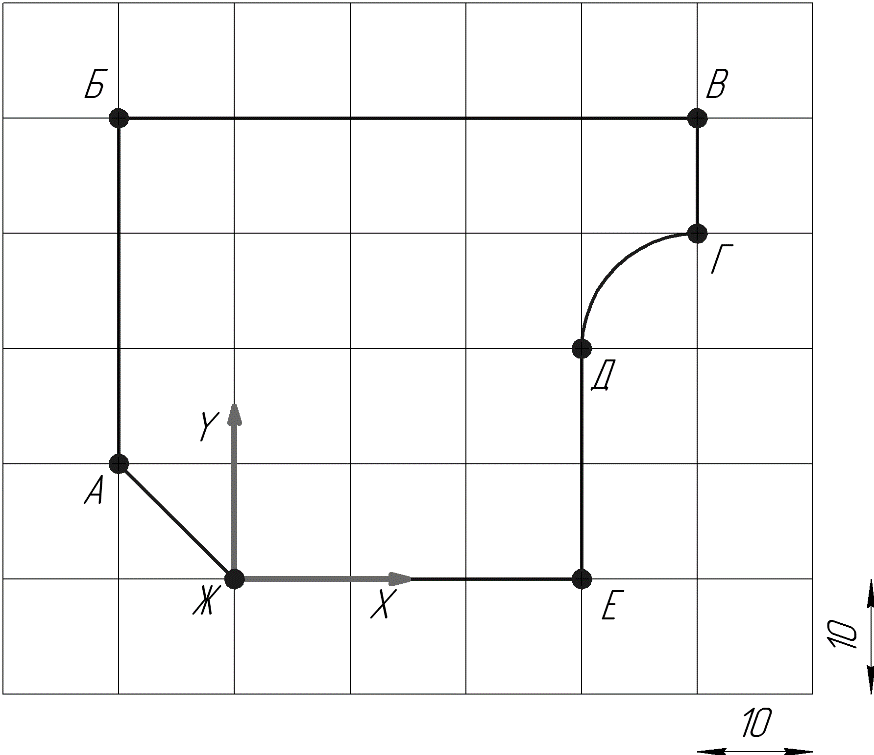
рис.6.
После скалывания координат опорных точек контура получим:
| Координаты точек | Запись в виде УП |
| т. А X-10 Y10 т. Б X-10 Y40 т. В X40 Y40 т. Г X40 Y30 т. Д X30 Y20 т. Е X30 Y0 т. Ж X0 Y0 | N1 G90 N2 X-10 Y10 N3 X-10 Y40 N4 X40 Y40 N5 X40 Y30 N6 X30 Y20 N7 X30 Y0 N8 X0 Y0 |
Относительная система счисления
1. Выполняем 1-2 пункты алгоритма решения задачи №1, получаем рисунок 6.
2. Скалываем координаты опорных точек:
2.1. Координаты первой точки, например т.А, берем относительно начала системы координат (рис.7). Получаем X-10 Y10.
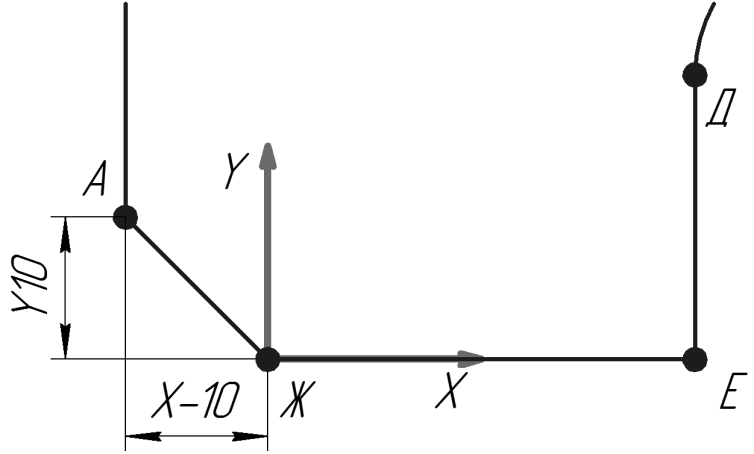
рис.7
2.2. Координаты второй точки, например т.Б, берем относительно точки А, как если бы центр координат переместился в т.А(рис.8). Получаем X0 Y30.
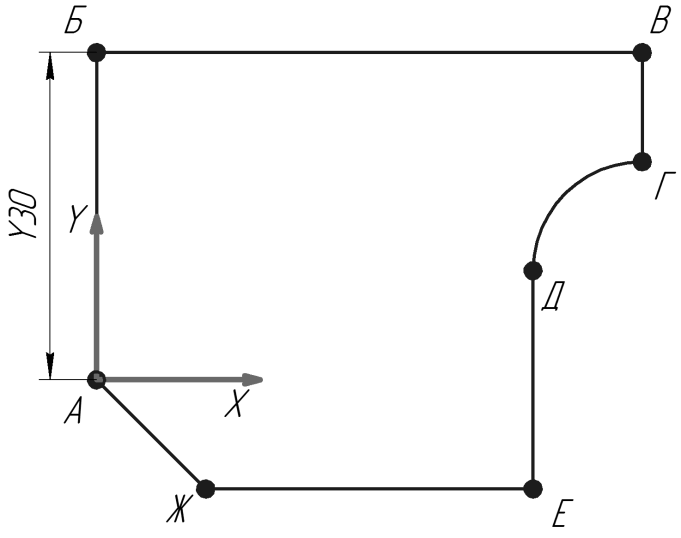
рис.8
2.3. Выполняем подобные действия для остальных опорных точек.
3. Записываем полученные координаты в виде УП
| Координаты точек | Запись в виде УП |
| т. А X-10 Y10 т. Б X0 Y30 т. В X50 Y0 т. Г X0 Y-10 т. Д X-10 Y-10 т. Е X0 Y-20 т. Ж X-30 Y0 | N1 G91 N2 X-10 Y10 N3 X0 Y30 N4 X50 Y0 N5 X0 Y-10 N6 X-10 Y-10 N7 X0 Y-20 N8 X-30 Y0 |
Задача №3. Рассчитать координаты точек в абсолютной (G90) системе счисления и относительной (G91) для различных нулевых точек (G54, G55)
Для контура (рис.9) рассчитать координаты точек в абсолютной (G90) системе счисления и относительной (G91) для различных нулевых точек (G54, G55)
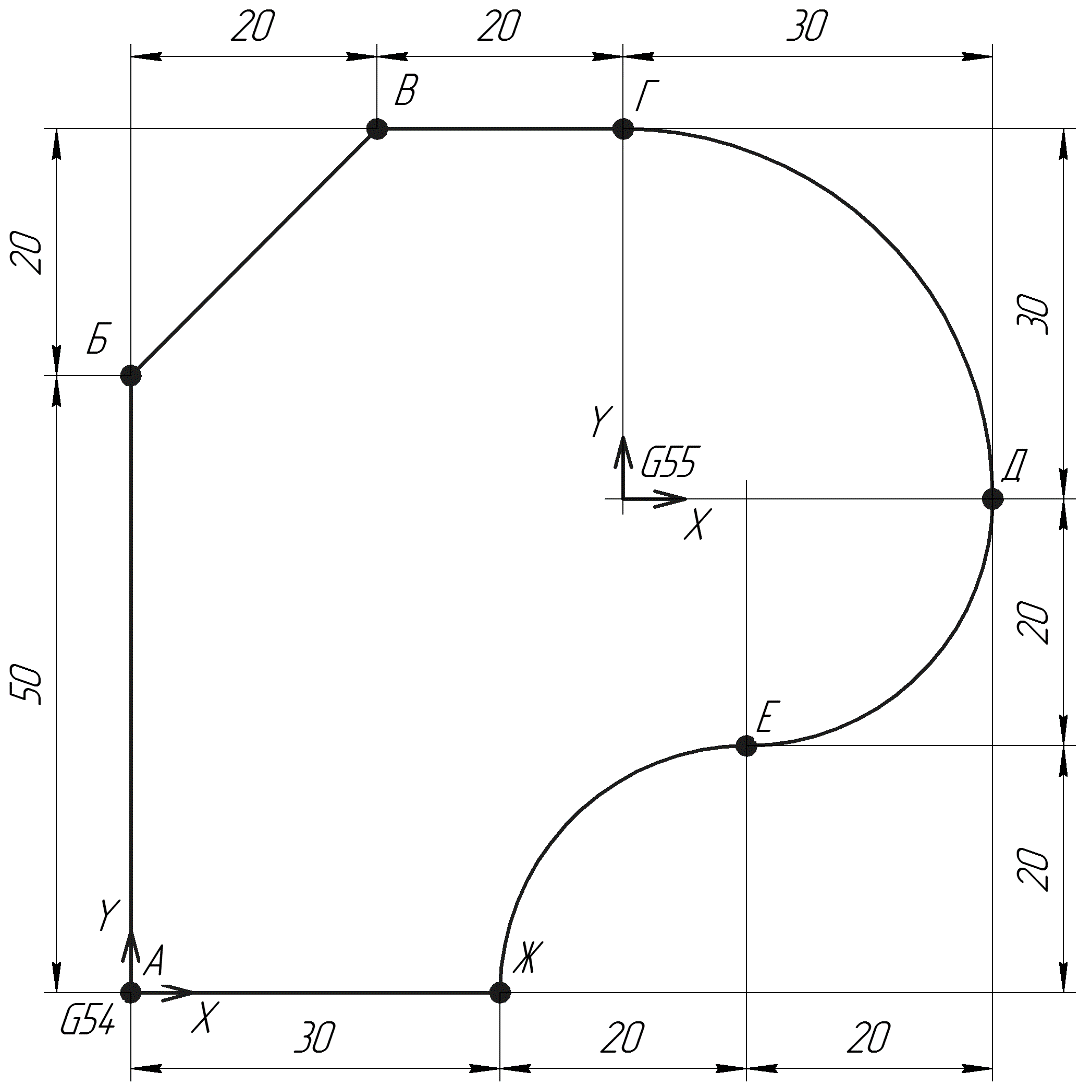
рис. 9
Алгоритм решения
Нулевая точка – G54
Абсолютная система счисления
Выполняем алгоритм решения аналогично задаче №1, но для контура рис.9. После скалывания координат получим:
| Координаты точек | Запись в виде УП |
| т. А X0 Y0 т. Б X0 Y50 т. В X20 Y70 т. Г X40 Y70 т. Д X70 Y40 т. Е X50 Y20 т. Ж X30 Y0 | N1 G90 G54 N2 X0 Y0 N3 X0 Y50 N4 X20 Y70 N5 X40 Y70 N6 X70 Y40 N7 X50 Y20 N8 X30 Y0 |
Относительная система счисления
Алгоритм решения подобен алгоритму задачи №2 для относительной системы счисления. После скалывания координат получим:
| Координаты точек | Запись в виде УП |
| т. А X0 Y0 т. Б X0 Y50 т. В X20 Y20 т. Г X20 Y0 т. Д X30 Y-30 т. Е X-20 Y-20 т. Ж X-20 Y-20 | N1 G91 G54 N2 X0 Y0 N3 X0 Y50 N4 X20 Y20 N5 X20 Y0 N6 X30 Y-30 N7 X-20 Y-20 N8 X-20 Y-20 |
Нулевая точка – G55
Абсолютная система счисления
Ход решения аналогичен примеру с нулевой точкой – G54, но в качестве центра системы координат принимаем точку, обозначенную как G55. После скалывания координат получим:
| Координаты точек | Запись в виде УП |
| т. А X-40 Y-40 т. Б X-40 Y10 т. В X-20 Y30 т. Г X0 Y30 т. Д X30 Y0 т. Е X10 Y-20 т. Ж X-10 Y-40 | N1 G90 G55 N2 X-40 Y-40 N3 X-40 Y10 N4 X-20 Y30 N5 X0 Y30 N6 X30 Y0 N7 X10 Y-20 N8 X-10 Y-40 |
Относительная система счисления
После скалывания координат получим:
| Координаты точек | Запись в виде УП |
| т. А X-40 Y-40 т. Б X0 Y50 т. В X20 Y20 т. Г X20 Y0 т. Д X30 Y-30 т. Е X-20 Y-20 т. Ж X-20 Y-20 | N1 G91 G55 N2 X-40 Y-40 N3 X0 Y50 N4 X20 Y20 N5 X20 Y0 N6 X30 Y-30 N7 X-20 Y-20 N8 X-20 Y-20 |
Примечание.
Можно заметить, что в относительной системе счисления значения координат точек Б-Ж одинаковы как при G54, так и при G55. Такое явление можно наблюдать из-за того, что в относительной системе счисления значения координат зависят от выбора первой точки и последовательности замеров. В нашем случае и при G54 и при G55 измерения начинались с т. А.
Задача №4. Рассчитать координаты точек в абсолютной системе счисления (G90) для различных плоскостей интерполяции G17 (XY), G18 (XZ), G19 (ZY).
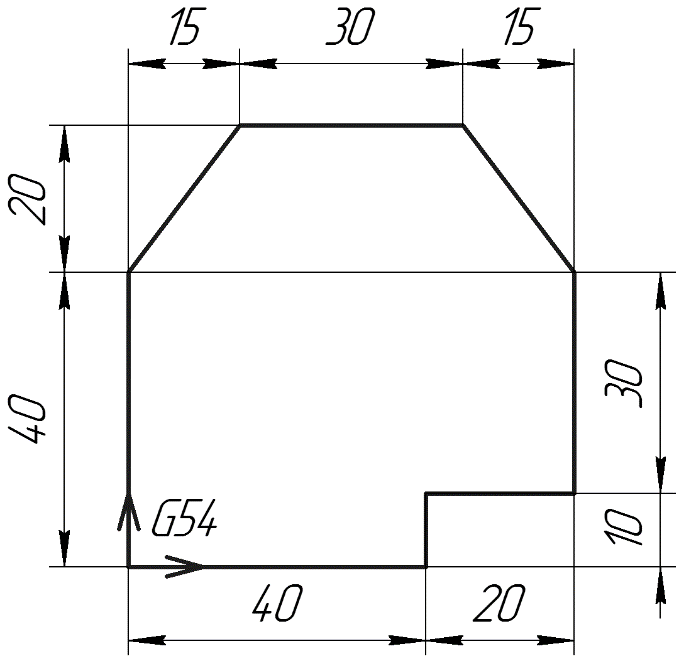
рис.10
| Запись в виде УП | ||
| G17 | G18 | G19 |
| N1 G90 G17 G54 N2 X0 Y0 N3 X0 Y40 N4 X15 Y60 N5 X45 Y60 N6 X60 Y40 N7 X60 Y10 N8 X40 Y10 N9 X40 Y0 | N1 G90 G18 G54 N2 X0 Z0 N3 X0 Z40 N4 X15 Z60 N5 X45 Z60 N6 X60 Z40 N7 X60 Z10 N8 X40 Z10 N9 X40 Z0 | N1 G90 G19 G54 N2 Y0 Z0 N3 Y0 Z40 N4 Y15 Z60 N5 Y45 Z60 N6 Y60 Z40 N7 Y60 Z10 N8 Y40 Z10 N9 Y40 Z0 |
